高校数学の数学Bについて公式をまとめました。
どうぞ!!
数学B
第1章 平面上のベクトル
語句まとめ:大きさ,向き
逆ベクトル:
\(\overrightarrow{a}=\overrightarrow{AB}\)のとき,
\(-\overrightarrow{a}=-\overrightarrow{AB}\)
ベクトルの加法:
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
ベクトルの加法の性質:
\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\) 交換法則
\(( \overrightarrow{a}+\overrightarrow{b} )+ \overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\) 結合法則
零ベクトルの性質:
\(\overrightarrow{a}(-\overrightarrow{a})=\overrightarrow{0}\),
\(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\)
ベクトルの減法:
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{BA}\)
\(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\),
ベクトルの実数倍,和の性質:
\(k(\overrightarrow{la})+(kl)\overrightarrow{a}\)
\((k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}\)
\(k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b}\)
ベクトルの平行条件:
\(\overrightarrow{a}\parallel \overrightarrow{b}\) \(\Longleftrightarrow\)\(\overrightarrow{b}=k\overrightarrow{a}\)となる実数\(k\)がある
単位ベクトル:
\(\overrightarrow{a}\)と平行な単位ベクトルは
\(\frac{\overrightarrow{a}}{| \overrightarrow{a} |}\)と\(-\frac{\overrightarrow{a}}{| \overrightarrow{a} |}\)
\(\overrightarrow{a}\)の大きさ:
\(\overrightarrow{a}=(a_1,a_2)\)のとき
\(| \overrightarrow{a} |=\sqrt{a_1^2+a_2^2}\)
実数倍,和の成分表示:
\(k(a_1,a_2)+g(b_1,b_2)=(ka_1+gb_1,ka_2+gb_2)\)
2点A(\(a_1,a_2\)),B(\(b_1,b_2\))について:
\(\overrightarrow{AB}=(b_1-a_1,b_2-a_2)\), \(|\overrightarrow{AB}|=\sqrt{(b_1-a_1)^2+
(b_2-a_2)^2}\)
ベクトルの内積:
\(\overrightarrow{a}・\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\theta\)
ただし,\(\theta\)は\(\overrightarrow{a}\)と\(\overrightarrow{b}\)のなす角
ベクトルの垂直と内積:
\(\overrightarrow{a}\perp \overrightarrow{b}\) \(\Longleftrightarrow\)\(\overrightarrow{a}・\overrightarrow{b}=0\)
内積と成分:
\(\overrightarrow{a}=(a_1,a_2),\overrightarrow{b}=(b_1,b_2)\)のとき
\(\overrightarrow{a}・\overrightarrow{b}=a_1b_1+a_2b_2\)
ベクトルのなす角の余弦:
\(\overrightarrow{a}=(a_1,a_2)\),\(\overrightarrow{a}=(b_1,b_2)\)のなす角を\(\theta\)とする。
\(cos\theta=\frac{\overrightarrow{a}・\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}\)
ベクトルの垂直条件:
\(\overrightarrow{a}=(a_1,a_2),\overrightarrow{b}=(b_1,b_2)\)
\(\overrightarrow{a}\perp \overrightarrow{b} \Longleftrightarrow\overrightarrow{a}・\overrightarrow{b}=0\)
内積の性質:
\(\overrightarrow{a}・\overrightarrow{a}=|\overrightarrow{a}|^2\)
\(\overrightarrow{a}・\overrightarrow{b}=\overrightarrow{b}・\overrightarrow{a}\)
\((\overrightarrow{a}+\overrightarrow{b})・\overrightarrow{c}=\overrightarrow{a}・\overrightarrow{c}+\overrightarrow{b}・\overrightarrow{c}\)
\(\overrightarrow{a}(\overrightarrow{b}・\overrightarrow{c})=\overrightarrow{a}・\overrightarrow{c}+\overrightarrow{b}・\overrightarrow{c}\)
\(\overrightarrow{ka}・\overrightarrow{b}=\overrightarrow{a}・\overrightarrow{kb}=k(\overrightarrow{a}・\overrightarrow{b})\) ただし,\(k\)は実数
内分点・外分点の位置ベクトル:
2点\(A(\overrightarrow{a}),B(\overrightarrow{b})\)に対して,線分ABを\(m,n\)に内分する点,\(m:n\)に内分する点の位置ベクトルは,
内分 \(\cdots \frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\)
外分 \(\cdots \frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\)
中点 \(\cdots \frac{\overrightarrow{a}+\overrightarrow{b}}{2}\)
3点A(\(\overrightarrow{a}\)),B(\(\overrightarrow{b}\)),C(\(\overrightarrow{c}\))を頂点とする\(\triangle\)ABCの重心Gの位置ベクトル\(\overrightarrow{g}\):
\(\overrightarrow{a}=\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)
三角形の中線:
三角形の重心は,3点の中線が交わる線で,各中線を2:1に内分する
1直線上にある点:
点Cが直線AB上にある \(\Longleftrightarrow\) \(\overrightarrow{AC}=k\overrightarrow{AB}\) となる実数\(k\)がある
点A(\(x_1,y_1\))を通り,\(\overrightarrow{d}=(l,m)\)に平行な直線の方程式:
\(m(x-x_1)-l(y-y_1)=0\)
異なる2点A(\(\overrightarrow{a}\)),B(\(\overrightarrow{b}\))を通る直線ABのベクトル方程式:
\(\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b}\)
\(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}, s+t=1\)
法線ベクトル:
点A(\(x_1,y_1\))を通り,\(\overrightarrow{n}=(a,b)\)に垂直な直線の方程式は
\(a(x-x_1)+b(y-y_1)=0\)
ベクトル \(\overrightarrow{a,b}\) は,直線 \(ax+by+c=0\) に垂直である
第2章 空間ベクトル
語句まとめ:\(xy\)平面,\(yz\)平面,\(zx\)平面
原点Oと点P(\(a,b,c\))の距離は:
\(OP=\sqrt{a^2+b^2+c^2}\)
ベクトルの大きさ:
\(\overrightarrow{a}=(a_1,a_2,a_3)\)の大きさは \(|\overrightarrow{a}|=
\sqrt{a_{1}^{2}a_{2}^{2}a_{3}^{2}}\)
和,実数倍の成分表示:
\( k(a_1,a_2,a_3)+g(b_1,b_2,b_3)= (ka_1+gb_1,ka_2+gb_2,ka_3+gb_3)\)
ただし,\(k,g\)は実数
2点A,Bとベクトル\(\overrightarrow{AB}\):
2点A(\(a_1,a_2,a_3\)),B(\(b_1,b_2,b_3\))について
\(\overrightarrow{AB}=(b_1-a_1,b_2-a_2,b_3-a_3)\)
\(|\overrightarrow{AB}|\sqrt{(b_1-a_1)^2(b_2-a_2)^2(b_3-a_3)^2}\)
ベクトルの内積:
\(\overrightarrow{a}=(a_1,a_2,a_3)\),\(\overrightarrow{b}=(b_1,b_2,b_3)\)のなす角\(\theta\)とするとき
\(\overrightarrow{a}・\overrightarrow{b}=a_1b_1+a_2b_2+a_3b_3\)
\(cos\theta =\frac{\overrightarrow{a}・\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}\)
ベクトルの垂直条件:
\(\overrightarrow{a}=(a_1,a_2,a_3)\),\(\overrightarrow{b}=(b_1,b_2,b_3)\)のとき
\(\overrightarrow{a}\perp \overrightarrow{b} \Longleftrightarrow \overrightarrow{a}・\overrightarrow{b}=0\)
位置ベクトル:
2点A(\(\overrightarrow{a}\)),B(\(\overrightarrow{b}\))
に対して \(\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}\)
2点A(\(\overrightarrow{a}\)),B(\(\overrightarrow{b}\))に対して,線分ABを\(m:n\)に内分する点,\(m:n\)に外分する点の位置ベクトル
内分 \(\cdots\) \(\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\)
外分 \(\cdots\) \(\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\)
中点 \(\cdots\) \(\frac{\overrightarrow{a}+\overrightarrow{b}}{2}\)
3点A(\(\overrightarrow{a}\)),B(\(\overrightarrow{b}\)),C(\(\overrightarrow{c}\))を頂点とする\(\triangle\)ABCの重心Gの位置ベクトル\(\overrightarrow{g}\):
\(\overrightarrow{g}=\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)
1直線上にある点->
同じ平面上にある点->
内積の利用->
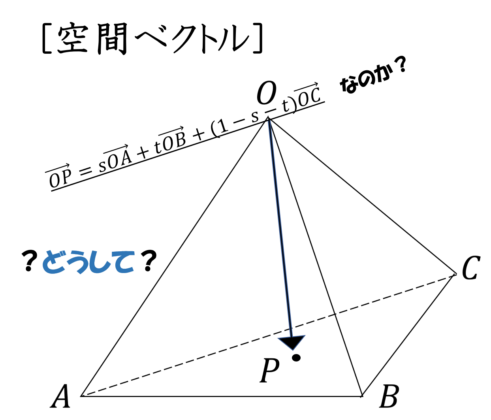
同じ平面上にある点:
一直線上にない3点A(\(\overrightarrow{a}\)),B(\(\overrightarrow{b}\)),C\(\overrightarrow{c}\)と点P(\(\overrightarrow{p}\))について
点Pが3点A,B,Cの定める平面ABC上にある
\(\Longleftrightarrow\) \(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}+u\overrightarrow{c}\), \(s+t+u=1\)となる実数\(s,t,c\)がある
2点間の距離と内分点・外分点の座標:
2点A\((a_1,a_2,a_3)\),B\((b_1,b_2,b_3)\)について
A,B間の距離:
\(AB=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2}\)
線分ABを\(m:n\)に内分する点の座標:
\((\frac{n\overrightarrow{a_1}+m\overrightarrow{b_1}}{m+n},\frac{n\overrightarrow{a_2}+m\overrightarrow{b_2}}{m+n},\frac{n\overrightarrow{a_3}+m\overrightarrow{b_3}}{m+n})\)
線分ABを\(m:n\)に外分する点の座標:
\((\frac{-n\overrightarrow{a_1}+m\overrightarrow{b_1}}{m-n},\frac{-n\overrightarrow{a_2}+m\overrightarrow{b_2}}{m-n},\frac{-n\overrightarrow{a_3}+m\overrightarrow{b_3}}{m-n})\)
座標平面に平行な平面の方程式:
点A(\(a\),0,0)を通り,\(yz\)平面に平行な平面の方程式は \(x=a\)
点B(0,\(b\),0)を通り,\(zx\)平面に平行な平面の方程式は \(y=b\)
点C(0,0,\(c\))を通り,\(zy\)平面に平行な平面の方程式は \(z=c\)
球面の方程式:
点(\(a,b,c\))を中心とする半径\(r\)の球面の方程式は\((x-a)^2+(y-b)^2+(z-c)^2=r^2\)
とくに,原点を中心とする半径\(r\)の球面の方程式は\(x^2+y^2+z^2=r^2\)
平面の方程式:
点A(\(x_1,y_1,z_1\))を通り,ベクトル\(\overrightarrow{n}=(a,b,c)\)に垂直な平面\(\alpha\)上の点をP(\(x,y,z\))とすると,平面\(\alpha\)の方程式
\(a(x-x_1)+b(y-y_1)+c(z-z_1)=0\)
第3章 数列
語句まとめ:初項,一般項,公差,項数,末項
等差数列の一般項:
初項\(a\),公差\(d\)の等差数列\({a_n}\)の一般項は
\(a_n=a+(n-1)d\)
等差数列の性質:
\(a_{n+1}=a_n+d\) すなわち \(a_{n+1}-a_n=d\)
等差数列の和:
等差数列の初項から第\(n\)項までの和を\(S_n\)とする
初項\(a\),第\(n\)項\(l\)のとき \(S_n=\frac{1}{2}n(a+l)\)
初項\(a\),公差\(d\)のとき \(S_n=\frac{1}{2}n{2a+(n-1)d}\)
等差数列の和の最大->
語句まとめ:等比数列,公比
等比数列の一般項:
初項\(a\),公比\(r\)の等比数列{\(a_n\)}の一般項
\(a_n=ar^{n-1}\)
等比数列の和:
初項\(a\),公比\(r\)の等比数列の初項から第\(n\)項までの和\(S_n\)は
\(r\neq 1\)のとき \(S_n=\frac{a(1-r^n)}{1-r} または S_n=\frac{a(r^n-1)}{r-1}\)
\(r=1\)のとき \(S_n=na\)
複利計算->
いろいろな数列->
和の記号:
初項から第\(n\)項¥までの和を,第\(k\)項\(a_k\)と和の記号\(\sum\)を用いて
\(\sum_{k=1}^{n}a_k=a_1a_2a_3+\cdots+a_n\)
自然数に関する和の公式:
\(\sum_{k=1}^{n}1=n\),\(\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)\),
\(\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)\),\(\sum_{k=1}^{n}k^3={ \frac{1}{2}n(n+1) }^2\)
和の記号の性質:
\(\sum_{k=1}^{n}(pa_k+qb_k)= p\sum_{k=1}^{n}a_k+q\sum_{k=1}^{n}b_k\)
ただし,\(p,q\)は\(k\)に無関係な定数
階差数列と一般項:
数列{\(a_n\)}の階差数列を{\(b_n\)}とすると
\(n\geq 2\)のとき \(a_n=a_1+\sum_{k=1}^{n-1}b_k\)
数列の和と一般項:
数列{\(a_n\)}と初項\(a_1\)から第\(n\)項までの和を\(S_n\)とすると
\(a_1=S_1\)
\(n\geq 2\)のとき \(a_n=S_n-S_{n-1}\)
いろいろな数列の和->
部分分数分解->
数学的帰納法->
等差数列と等比数列の漸化式:
等差数列{\(a_n\)}の漸化式は \(a_{n+1}=a_n+d\)
等比数列{\(a_n\)}の漸化式は \(a_{n+1}=ra_n\)
階差数列と一般項:
数列{\(a_n\)}の階差数列を{\(b_n\)}とすると
\(n\geq 2\)のとき \(a_n=a_1+\sum_{k=1}^{n-1}b_k\)
\(a_{n+1}=pa_n+q\)を満たす数列の階差数列->
隣接3項間の漸化式->
数学的帰納法の原理:


等式の証明->
不等式の証明->
整数の性質の証明->
第4章 確率分布と統計的な推測
語句まとめ:期待値,平均
確率の総和:
確率変数\(X\)のとりうる値\(x_k\)が起こる確率を\(p_k\)とすると\(p_1\)から\(p_n)までの総和は
$$\sum_{k=1}^{n} p_k=p_1+p_2+\cdots+p_n=1$$
確率変数の期待値(平均):
確率変数\(X\)の期待値\(E(X)\)は
\(E(X)=\sum_{k=1}^{n} x_kp_k=x_1p_1+x_2p_2+\cdots+x_np_n\)
確率変数\(X^2\)の期待値\(E(X^2)\):
\(E(X^2)=\sum_{k=1}^{n}x_k^2p_k \)
確率変数の分散\(V(X)\):
確率変数\(X\)の期待値を\(m\)とするとき,分散\(V\)は,確率変数\((X-m)^2\)の期待値で定義され,
$$V(X)=E((X-m)^2)=\sum_{k=1}^{n}(x_k-m)^2p_k=(x_1-m)^2p_1+(x_2-m)^2p_2+\cdots+(x_n-m)^2p_n$$
\(aX+b\)の期待値\(E(aX+b)\):
\(X\)を確率変数,\(a,b\)を定数とすると,
$$E(aX+b)=aE(X)+b$$
分散と期待値の関係:
確率変数\(X\)について \(V(X)=E(X^2)-{ E(X) }^2\)
標準偏差:
\(\sigma=\sqrt{V(X)}\)
\(aX+b\)の分散:
\(X\)を確率変数,\(a\),\(b\)を定数とするとき
\(V(aX+b)=a^2V(X)\), \(\sigma(aX+b)=| a |\sigma(X)\)
2つの確率変数の和の期待値:
\(E(X+Y)=E(X)+E(Y)\)
\(aX+bY\)の期待値:
\(E(aX+bY)=aE(X)+bE(Y)\)
独立な2つの確率変数の積の期待値:
2つの確率変数\(X,Y\)が互いに独立であるとき
\(E(XY)=E(X)E(Y)\)
独立な2つの確率変数の和の分散:
2つの確率変数\(X,Y\)が互いに独立であるとき
\(V(X+Y)=V(X)+V(Y)\)
3つ以上の確率変数の独立:
\(E(XYZ)=E(X)E(Y)E(Z)\)
\(V(X+Y+Z)=V(X)+V(Y)+V(Z)\)
語句まとめ:二項分布,正規分布,連続型確率変数
1回の試行で事象\(A\)が起こる確率を\(p\)とする。この試行を\(n\)回行う反復試行において,\(A\)がちょうど\(r\)回起こる確率は
$${}_n\mathrm{C}_r p^r(1-p)^{n-r}$$
二項分布に従う確率変数の期待値と分散:
確率変数\(X\)が二項分布\(B(n,p)\)に従うとき
\(E(X)=np\), \(V(X)=np(1-p)\), \(\sigma(X)=\sqrt{np(1-p)}\)
確率密度関数\(f(x)\)の性質:
常に\(f(x)\geq 0\)で \(P(a \leq X \leq)=\int_a^b f(x)dx\)
\(X\)のとる範囲が\(\alpha \leq X \leq \beta\)のとき\(\int_{\alpha}^{\beta}f(x)dx=1\)
正規分布の確率密度関数\(f(x)\):
確率変数\(X\)が正規分布\(N(m,\sigma^2)\)に従うとき
\(f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-m)^2}{2\sigma^2}}\)
正規分布の期待値,標準偏差:
確率変数\(X\)が正規分布\(N(m,\sigma^2)\)に従うとき
\(E(X)=m,\sigma(X)=\sigma\)
標準正規分布の確率密度関数\(f(z)\):
確率変数\(X\)が正規分布\(N(0,1)\)に従うとき,
\(f(z)=\frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}\)
正規分布と標準正規分布:
確率変数\(X\)が正規分布\(N(m,\sigma^2)\)に従うとき
$$Z=\frac{X-m}{\sigma}$$
二項分布の正規分布による近似:
二項分布\(B(n,p)\)に従う確率変数\(X\)は,\(n\)が大きいとき,近似的に正規分布\(N(np,np(1-p))\)に従う
連続型確率変数\(f(x)\)の期待値と分散
連続型確率変数\(f(x)\)の期待値\(m=E(X)\)と標準偏差\(\sigma\)
連続型変数\(X\)がとり得る値の範囲が\(\alpha\leq X \leq \beta\)のとき,
$$m=E(X)=\int_{\alpha}^{\beta}xf(x) dx$$
$$V(X)=\int_{\alpha}^{\beta}(x-m)^2 f(x)dx$$
語句まとめ:母集団,標本,無作為抽出,無作為標本,復元抽出,非復元抽出,母平均,母分散,母比率,標本平均,標本分散,標本比率,
標本平均の期待値と標準偏差:
母平均\(m\),母分散\(\sigma^2\)の母集団から大きさ\(n\)の無作為標本を抽出するとき,その標本平均\(\overline{X}\)の期待値\(E(\overline{X})\)と分散\(S(\overline{X})\)は
\(E(\overline{X})=m, S(\overline{X}=\frac{\sigma^2}{n})\)
標本平均の分布:
母平均\(m\),母分散\(\sigma^2\)の母集団から抽出された大きさ\(n\)の無作為標本について,標本平均\(\overline{X}\)は,\(n\)が大きいとき,近似的に正規分布
\(N(m,\frac{\sigma^2}{n})\)に従うと見なすことがある
標本比率の分布:
特性Aの母比率\(p\)の母集団から抽出された大きさ\(n\)の無作為標本について,標本比率\(R\)は,\(n\)が大きいとき,近似的に正規分布\(N(p,\frac{p(1-p)}{n})\)に従うと見なすことがある
大数の法則:
母平均\(m\)の集団から大きさ\(n\)の無作為標本を抽出するとき,\(n\)が大きくなるに従って,その標本平均\(\overline{X}\)はほとんど確実に母平均\(m\)に近づく
母平均の推定:
母分散を\(\sigma^2\)とする。標本の大きさ\(n\)が大きいとき,母平均\(m\)に対する信頼度95%の信頼区間は
$$[ \overline{X}-1.96・\frac{\sigma}{\sqrt{n}},\overline{X}+1.96・\frac{sigma}{\sqrt{n}}]$$
母比率の推定:
標本の大きさ\(n\)が大きいとき,標本比率を\(p\)とすると,母比率\(\hat{p}\)に対する信頼度95%の信頼区間は
$$[ p-1.96・\sqrt{\frac{p(1-p)}{n}},p+1.96・\sqrt{\frac{p(1-p)}{n}} ]$$
数学B演習問題リンク集
数列の記事




空間ベクトルの記事