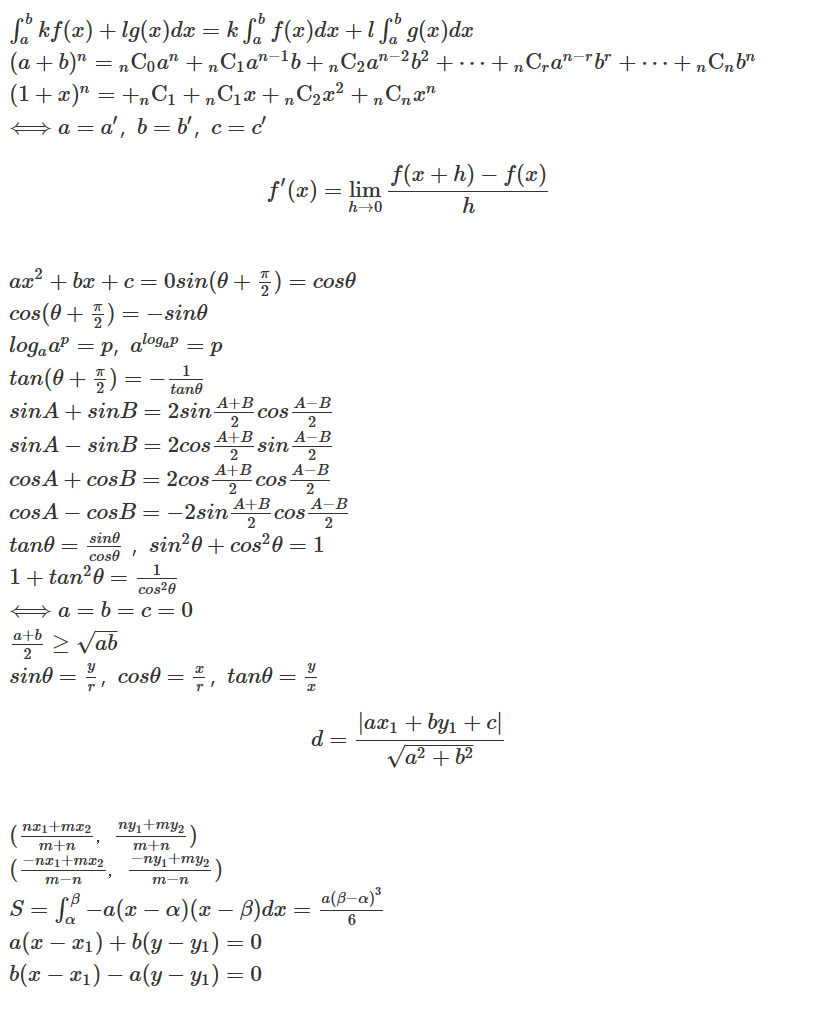どうも,ユキです。
高校数学の数学2について公式をまとめました。
どうぞ!!
数学Ⅱ
第1章 式と証明
3次式の展開と因数分解:
\((a+b)^3=a^3+3a^2b+3ab^2+b^3\),\((a-b)^3=a^3-3a^2b+3ba^2-b^3\)
展開の公式:
\((a+b)(a^2-ab+b^2)=a^3+b^3\),\((a-b)(a^2+ab+b^2)=a^3-b^3\)
因数分解の公式:
\(a^3+b^3=(a+b)(a^2-ab+b^2)\),\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
二項定理:
\((a+b)^n={}_n\mathrm{C}_0a^n+{}_n\mathrm{C}_1a^{n-1}b+{}_n\mathrm{C}_2a^{n-2}b^2+\cdots+{}_n\mathrm{C}_ra^{n-r}b^r+\cdots+{}_n\mathrm{C}_nb^n \)
二項定理の応用:
\((1+x)^n=+{}_n\mathrm{C}_1+{}_n\mathrm{C}_1x+{}_n\mathrm{C}_2x^2+{}_n\mathrm{C}_nx^n\)
\((a+b+c)^n\)の展開式:
\((a+b+c)^n\)の展開式における\(a^pb^qc^r\)の項の係数は
\(\frac{n!}{p!q!r!}\) ただし \(p+q+r=n\)
語句まとめ:整式
\(A=BQ+R\):
\(A\),\(B\)が整式とすると,\(A\)を\(B\)で割った商は\(Q\)となり,余りは\(R\)となる。
とくに,
\(A=BQ\)のとき:
つまり,\(R=0\)のときは\(A\)は\(B\)で割り切れるという
分数式の約分:
\(\frac{A}{B}=\frac{AC}{BC}\) (ただし \(C \neq 0 \))
分数式の四則演算:
\(\frac{A}{B}\times\frac{C}{D}=\frac{AC}{BD}\)
分数式の加法・減法:
\(\frac{A}{C}+\frac{B}{C}=\frac{A+B}{C}\)
語句まとめ:恒等式
恒等式の性質:
\(ax^2+bx+c=a’x^2+b’x+c’\)が\(x\)についての恒等式
\(\Longleftrightarrow\) \(a=a’\),\(b=b’\),\(c=c’\)
\(ax^2+bx+c=0\)が\(x\)についての恒等式
\(\Longleftrightarrow\) \(a=b=c=0\)
代入による恒等式の係数決定->
恒等式に関する証明->
\(A=B\)の証明方法:
1 \(A\)か\(B\)の一方を変形して,他方を導く
2 \(A\)と\(B\)の両方を変形して,同じ式を導く
3 \(A-B\)を変形して,0になることを示す
条件付きの等式の証明->
条件が比例式の等式の証明->
不等式の証明->
実数の大小関係:
\(a>b\), \(b>c\) \(\Rightarrow\) \((a>c)\)
\(a>b\) \(\Rightarrow\) \(a+c>b+c,a-c>b-c\)
\(a>b\), \(c>0\) \(\Rightarrow\) \(\frac{a}{c}>\frac{b}{c}\)
\(a>b\), \(c<0\) \(\Rightarrow\) \(\frac{a}{c}<\frac{b}{c}\)
2数の大小関係と差:
\(a>b\) \(\Longleftrightarrow\) \(a-b>0\)
\(a<b\) \(\Longleftrightarrow\) \(a-b<0\)
実数の平方の性質:
実数\(a\)について \(a^2 \geq 0\)
等号が成り立つのは,\(a=0\)のとき
実数\(a,b\)について \(a^2+b^2 \geq 0\)
等号が成り立つのは,\(a=b=0\)のとき
相加平均:
\(\frac{a+b}{2}\)を\(a\)と\(b\)の相加平均という
相乗平均:
\(a>0\),\(b>0\)のとき,\(\sqrt{ab}\)を\(a\)と\(b\)の相乗平均という
相加平均と相乗平均の大小関係:
\(\frac{a+b}{2}\geq \sqrt{ab}\)
等号成立は,\(a=b\)のときである
第2章 複素数と方程式
複素数の相等:
\(a+bi=c+di\) \(\Longleftrightarrow\) \(a=c\)かつ\(b=d\)
とくに\(a+bi=0\) \(\Longleftrightarrow\) \(a=0\) かつ \(b=0\)
語句まとめ:共役な複素数
負の数の平方根:
\(a>0\) \(-a\)の平方根は\(\pm \sqrt{-a}=\pm \sqrt{a}i\)である
2次方程式の解の公式:
\(ax^2+bx+c=0\)の解は \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
2次方程式の解の種類の判別:
\(ax^2+bx+c=0\)の判別式を\(D\)とすると,
\(D>0\) \(\Longleftrightarrow\) 異なる2つの実数解
\(D=0\) \(\Longleftrightarrow\) 重解
\(D<0\) \(\Longleftrightarrow\) 異なる2つの虚数解
解と係数の関係:
\(ax^2+bx+c=0\)の2つの解を\(\alpha\),\(\beta\)とすると
\(\alpha+\beta=-\frac{b}{a}\),\(\alpha\beta=\frac{c}{a}\)
\(ax^2+bx+c=0\)が2つの解\(\alpha\),\(\beta\)を持つとき
\(ax^2+bx+c=a(x-\alpha)(x-\beta)\)
\(\alpha\),\(\beta\)を解とする2次方程式
\(\alpha\),\(\beta\)を解とする2次方程式の1つは
\(x^2-(\alpha+\beta)x+\alpha\beta=0\)
2次方程式の実数解の符号:
1 \(ax^2+bx+c=0\)の2つの解\(\alpha\),\(\beta\)と判別式\(D\)について
2 \(\alpha\),\(\beta\)は異なる2つの正の解\(\Longleftrightarrow\)
\(D>0\)で,\(\alpha+\beta > 0\)かつ\(\alpha\beta>0\)
3 \(\alpha\),\(\beta\)は異なる2つの負の解\(\Longleftrightarrow\) \(D>0\)で,
\(\alpha+\beta > 0\)かつ\(\alpha\beta>0\)
\(\alpha\),\(\beta\)は符号の異なる解\(\Longleftrightarrow\) \(\alpha\beta<0\)
剰余の定理と因数定理:
\(P(x)=(x-k)Q(x)+R\)
\(x=k\)のとき,\(P(k)=R\)
剰余の定理:
整式\(P(x)\)を\((x-k)\)で割ったあまりは,\(P(k)\)に等しい
因数定理:
整式\(P(x)\)が\(x-k\)で割り切れる \(\Longleftrightarrow\) \(P(k)=0\)
組立除法->
高次方程式->
第3章 図形と方程式
語句まとめ:内分,外分,象限
線分の内分点・外分点:
線分\(m:n\)を内分する点をP,外分する点Q
Pの座標\(\frac{na+mb}{m+n}\),外分点Qの座標は\(\frac{-na+mb}{m-n}\)
線分ABの中点の座標は\(\frac{a+b}{2}\)
<補足>内分点の座標で\(n\)を\(-n\)に置き換えたものが,外分点の座標
2点間の距離:
2点A(\(x_1,y_1)\),B(\(x_2,y_2\))間の距離ABは
$$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
原点OとA(\(x_1,y_1)\)の距離OAは
$$OA=\sqrt{x_1^2+y_1^2}$$
内分点,外分点の座標:
2点A(\(x_1,y_1\)),B(\(x_2,y_2\))を結ぶ線分ABを,\(m:n\)に内分する点をP,外分する点Qとする
Pの座標 \(( \frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n})\)
Qの座標 \(( \frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n})\)
線分ABの中点の座標 \((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2} )\)
重心の座標:
3点A(\(x_1,y_1\)),B(\(x_2,y_2\)),C(\(x_3,y_3\))を頂点とする
\(\triangle\)ABCの重心の座標
\(( \frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3} )\)
直線の方程式(1):
点(\(x_1,y_1\))を通り,傾きが\(m\)の直線の方程式
\(y-y_1=m(x-x_1)\)
直線の方程式(2):
異なる2点(\(x_1,y_1\)),(\(x_2,y_2\))を通る直線の方程式
\(x_1\neq x_2 y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)
\(x_1=x_2 x=x_1\)
2直線の平行,垂直:
2直線\(y=m_1x+k_1\),\(y=m_2x+k_2\)について
\(m_1=m_2\) \(\Longleftrightarrow\) 2直線が平行
\(m_1m_2=-1\) \(\Longleftrightarrow\) 2直線が垂直
点(\(x_1,y_1\))を通り,直線\(ax+by+c=0\)に平行な直線,垂直な直線:
平行 \(a(x-x_1)+b(y-y_1)=0\)
垂直 \(b(x-x_1)-a(y-y_1)=0\)
直線に対して対称な点:


点と直線の距離:
$$d=\frac{| ax_1+by_1+c |}{\sqrt{a^2+b^2}}$$
円の方程式:
点(\(a,b\))を中心とする半径\(r\)の円の方程式
\((x-a)^2+(y-b)^2=r^2\)
\(x^2+y^2+lx+my+n=0\)の表す図形->
円と直線:
\(D\)の符号\(D>0\) \(D=0\) \(D<0\)
\(ax^2+bx+c=0\)の実数解 異なる2つの実数解 重解(1つの解) なし
円と直線の位置関係 異なる2点で交わる 接する 共有点を持たない
共有点の個数 2個 1個 0個
\(d\)と\(r\)の大小:
\(d<r\) \(d=r\) \(d>r\)
円と直線の位置関係 異なる2点で交わる 接する 共有点を持たない
円上の点における接線の方程式:
円\(x^2+y^2=r^2\)上の点P(\(x_1,y_1\))における接線の方程式
$$x_1x+y_1y=r^2$$
2つの円の位置関係->
2つの円の共有点の座標->
2つの円の交点を通る図形->
軌跡を求める手順:
1 点P(\(x,y\))として,Pの条件を\(x,y\)の式で表す
2 逆に,1で求めた図形上のすべての点Pが,与えられた条件を満たすことを確かめる
線分の中点の軌跡:
Q(\(s,t\)),P(\(x,y\))とする。Qの満たす条件を表す\(s,t\)の式と,QとPの座標の関係式から,\(x,y\)の方程式を導く。
直線と領域:
直線\(\ell\):\(y=mx+k\)
1 \(y>mx+k\)の表す領域は,直線\(l\)の上側の部分
2 \(y<mx+k\)の表す領域は,直線\(l\)の下側の部分
円と領域:
1 \(x^2+y^2<r^2\)の表す領域は,円\(x^2+y^2=r^2\)の内部
2 \(x^2+y^2>r^2\)の表す領域は,円\(x^2+y^2=r^2\)の外部
連立不等式の表す領域->
領域の最大・最小->
領域を利用した証明->
\(p\)ならば\(q\) \(\Longleftrightarrow\) \(P\subset Q\)
放物線を境界線とする領域:
曲線\(F\):\(y=ax^2+bx+c\)
\(y>ax^2+bx+c\)の表す領域は,曲線\(F\)の上側の部分
\(y<ax^2+bx+c\)の表す領域は,曲線\(F\)の下側の部分
第4章 三角関数
語句まとめ:動径,始線
動径の表す角:
動径OPと始線OXのなす角の1つを\(\alpha\)とすると,動径OPの表す角は\(\alpha+360^\circ \times n\)。\(n\)は整数
語句まとめ:弧度法,度数法
弧度法と扇形:
半径\(r\),中心核\(\theta\)(ラジアン)の扇形の弧の長さ\(l\),面積\(S\)は
\(l=r\theta\), \(S=\frac{1}{2}r^2\theta\)
\(\theta\)の三角関数:
\(sin \theta=\frac{y}{r}\),\(cos \theta=\frac{x}{r}\),\(tan \theta=\frac{y}{x}\)
\(\theta\)の正弦,余弦,正接という
語句まとめ:単位円
三角関数の相互関係:
\(tan \theta=\frac{sin \theta}{cos \theta}\) ,\(sin^2\theta+cos^2\theta=1\)
\(1+tan^2\theta=\frac{1}{cos^2\theta}\)
三角関数のグラフ:
\(sin \theta\)の性質:
\(sin \theta\)の値は,P(\(x,y\))の\(y\)座標に等しい
\(y=sin\theta\)のグラフは原点に対して対称
周期は2\(\pi\)
\(cos \theta\)の性質:
\(sin \theta\)の値は,P(\(x,y\))の\(x\)座標に等しい
\(y=sin\theta\)のグラフは\(y\)軸に対して対称
周期は2\(\pi\)
\(tan\theta)の性質:
\(tan \theta\)の値は,T(\(1,m\))の\(y\)座標に等しい
\(tan (\theta+\pi)=tan \theta\)が成立
グラフは原点に対して対称
周期は\(\pi\)
三角関数で成り立つ等式:
\(sin (\theta+2n\pi)=sin \theta\)
\(cos (\theta+2n\pi)=cos \theta\)
\(tan (\theta+n\pi)=tan \theta\)
三角関数のグラフの対称性:
\(sin (-\theta)=-sin \theta\)
\(cos (-\theta)=sin \theta\)
\(tan (-\theta)=-tan \theta\)
\(sin (\theta+\pi)=-sin \theta\)
\(cos (\theta+\pi)=-cos \theta\)
\(tan (\theta+\pi)=tan \theta\)
\(sin (\theta+\frac{\pi}{2})=cos \theta\)
\(cos (\theta+\frac{\pi}{2})=-sin \theta\)
\(tan (\theta+\frac{\pi}{2})=-\frac{1}{tan \theta}\)
三角関数を含む方程式->
三角関数を含む不等式->
三角関数を含む関数の最大値,最小値->
正弦,余弦の加法定理:
\(sin(\alpha+\beta)=sin \alpha cos \beta+cos \alpha sin \beta\)
\(sin(\alpha-\beta)=sin \alpha cos \beta-cos \alpha sin \beta\)
\(cos(\alpha+\beta)=cos \alpha cos \beta-sin \alpha sin \beta\)
\(cos(\alpha-\beta)=cos \alpha cos \beta+sin \alpha sin \beta\)
正接の加法定理:
\(tan(\alpha+\beta)=\frac{tan \alpha+tan \beta}{1-tan \alpha tan \beta}\)
\(tan(\alpha-\beta)=\frac{tan \alpha-tan \beta}{1+tan \alpha tan \beta}\)
正弦,余弦の2倍角の公式:
\(sin 2\alpha=2sin \alpha cos \alpha\)
\(cos 2\alpha=cos^2\alpha-sin^2\alpha\)
\(cos 2\alpha=1-2sin^2\alpha\)
\(cos 2\alpha=2cos^2\alpha-1\)
正弦,余弦の半角の公式:
\(sin^2 \frac{\alpha}{2}=\frac{1-cos\alpha}{2}\),\(cos^2 \frac{\alpha}{2}=\frac{1+cos\
alpha}{2})
正接の2倍角,半角の公式:
\(tan 2\alpha=\frac{2tan\alpha}{1-tan^2\alpha}\),\(tan^2\frac{\alpha}{2}=\frac{1-cos \alpha}{1+cos \alpha}\)
三角関数の合成:
\(a sin \theta+b sin \theta=\sqrt{a^2+b^2} sin(\theta+\alpha)\)
ただし,\(cos\alpha=\frac{a}{\sqrt{a^2+b^2}},sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)
正弦,余弦の積を和や差に変形する4つの公式:
\(sin\alpha cos \beta=\frac{1}{2}{sin(\alpha+\beta)+sin(\alpha-\beta)}\)
\(cos\alpha sin \beta=\frac{1}{2}{sin(\alpha+\beta)-sin(\alpha-\beta)}\)
\(cos\alpha cos \beta=\frac{1}{2}{cos(\alpha+\beta)+cos(\alpha-\beta)}\)
\(sin\alpha sin \beta=\frac{1}{2}{cos(\alpha+\beta)-cos(\alpha-\beta)}\)
正弦,余弦の和や差を積に変形する4つの公式:
上の4つの公式において,\(\alpha+\beta=A\),\(\alpha-\beta=B\)とおくと,
\(sin A+sin B=2sin \frac{A+B}{2}cos \frac{A-B}{2})
\(sin A-sin B=2cos \frac{A+B}{2}sin \frac{A-B}{2})
\(cos A+cos B=2cos \frac{A+B}{2}cos \frac{A-B}{2})
\(cos A-cos B=-2sin \frac{A+B}{2}cos \frac{A-B}{2})
第5章 指数関数
累乗(1)
\(a^0=1,a^{-n}=\frac{1}{a^n}\) \(a^{-1}=\frac{1}{a}\)
累乗(2):
\(a^{\frac{1}{n}}=\sqrt[n]{a}\),\(a^{\frac{m}{n}}=(\sqrt[n]{a})^m=\sqrt[n]{a^m}\),\(a^{-r}
=\frac{1}{a^r}\)
指数法則(指数が有理数):
\(r\),\(s\)は有理数
\(a^r\times a^s=a^{r+s}\) \(\frac{a^r}{a^s}=a^{r-s}\)
\((a^r)^s=a^{rs}\) \((ab)^r=a^rb^r\)
語句まとめ:指数関数,増加関数,減少関数
指数関数\(y=a^x\)の特徴:
定義域:実数全体,値域:正の数全体
\(a>1\)のとき,増加関数
\(r<s \Longleftrightarrow a^r<a^s\)
\(0<a<1\)のとき,減少関数
\(r<s \Longleftrightarrow a^r>a^s\)
指数関数を含む方程式,不等式->
語句まとめ:底,対数,真数
指数と対数:
\(M>0\)とすると
\(M=a^p \Longleftrightarrow log_aM=p\)
\(log_aa^p=p\),\(a^{log_ap}=p\)
対数の性質(1):
\(log_a1=0\),\(log_aa=1\)
対数の性質(2):
\(M>0,N>0\)で\(k\)は実数
\(log_aMN=log_aM+log_aN\) \(log_a\frac{M}{N}=log_aM-log_aN\)
\(log_aM^k=klog_aM\)
底の変換公式:
\(a,b,c\)は正の数,\(a\neq 1\),\(b\neq 1\),\(c\neq 1\)とするとき
\(log_ab=\frac{log_cb}{logca}\) とくに\(log_ab=\frac{1}{log_ba}\)
対数関数\(y=log_ax\)の特徴:
定義域は正の数全体,値域は実数全体
\(a>1\)のとき,増加関数。すなわち
\(0<p<q \Longleftrightarrow log_ap<log_aq\)
\(0<a<1\)のとき,減少関数。すなわち
\(0<p<q \Longleftrightarrow log_ap>log_aq\)
対数関数を含む方程式,不等式->
対数を含む関数の最大値,最小値-?
常用対数->
桁数と常用対数の値の関係:
自然数\(N\)が\(m\)桁のかずであるとは,\(N\)が
\(10^{m-1} \leq N<10^m \)
を満たす。常用対数をとると,
\(m-1\leq log_{10}N<m\)
第6章 微分法と積分法
語句まとめ:平均変化率,極限値,微分係数
極限値:
関数\(f(x)\)において,\(x\)が\(a\)に近づくとき,\(f(x)\)の値が定数\(a\)に近づくならば,\(\alpha\)を\(f(x)\)の極限値という。このことを次のように書く。
\(\lim_{x \to a} f(x)=\alpha\)
\(f(x)\)の\(x=a\)における微分係数:
\(f’(a)=\lim_{h \to 0}\frac{f(a+h)^f(a)}{h}\)
接戦の傾きと微分係数:
関数\(y=f(x)\)のグラフ上の点\(A(a,f(a))\)における接線の傾きは,関数\(f(x)\)の\(x=a\)における微分係数\(f’(a)\)に等しい
導関数\(f’(x)\):
$$f’(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
関数\(x^n\)の導関数:
\((x^n)’=nx^{n-1}\)
\((c)’=0\)
定数倍,和の導関数:
\(k\)は定数
\(y=kf(x)+lg(x)\)を微分
\(y’=kf’(x)+lg’(x)\) \(k,l\)は定数
接線の方程式:
関数\(y=f(x)\)のグラフの点(\(a,f(a))\)における接線の方程式
\(y-f(a)=f’(a)(x-a)\)
\(f(x)\)の増減と\(f’(x)\)の符号:
\(f’(x)>0\)となる\(x\)の値の範囲では増加\(f’(x)<0\)となる\(f(x)<0\)となる\(x\)の値の範囲では減少
語句まとめ:増減表,極大,極大値, 極小, 極小値,極値
\(f(x)\)が極値をとるための十分条件:
\(f(x)\)が\(x=a\)で極地をとるならば,\(f’(a)=0\)である
<補足>逆は成り立たない
関数の最大・最小->
方程式への応用->
不等式への応用->
語句まとめ:原始関数,積分定数,不定積分
\(f(x)\)の不定積分:
\(F’(x)=f(x)\)のとき
\(\int f(x)dx=F(x)+C\) ただし,\(C\)は積分定数
\(x^n\)の不定積分:
\(\int x^ndx=\frac{1}{n+1}x^{n+1}+C\)
定数倍,和の不定積分:
\(F’(x)=f(x),G’(x)=g(x)\)のとき
\(\int kf(x)+lg(x)dx=kF(x)+lG(x)+C\) \(k\),\(l\)は定数
定積分:
\(F’(x)=f(x)\)のとき
\(\int_{a}^{b}f(x)dx=[ F(x) ]_a^b=F(b)-F(a)\)
関数の定数倍,和の定積分:
\(\int_{a}^{b}kf(x)+lg(x)dx=k\int_{a}^{b}f(x)dx+l\int_{a}^{b} g(x)dx \)
定積分の性質:
1 \(\int_{a}^{a}f(x)=0\)
2 \(\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx\)
3 \(\int_{a}^{b}f(x)dx=\int_{a}^{c}f(x)dx+\int_{c}^{b}f(x)dx\)
\(a\)を定数とするとき,
4 \(\frac{d}{dx}\int_{a}^{x}f(t)dt=f(x)\)
定積分と図形の面積:
\(a\leq x\leq b\)の範囲で\(f(x)\geq g(x)\)のとき,\(y=f(x)\)のグラフと\(x\)軸および2直線\(x=a,x=b\)で囲まれた部分の面積\(S\)は
\(S=\int_{a}^{b}{f(x)-g(x)}dx\)
曲線と接線で囲まれた図形の面積->
語句まとめ:切り取る線分の長さ
放物線\(y=a(x-\alpha)(x-\beta)\)と\(x\)軸で囲まれた部分の面積:
\(S=\int_{\alpha}^{\beta}-a(x-\alpha)(x-\beta)dx=\frac{a(\beta-\alpha)^3}{6}\)
[affi id=17]