今日の記事は、前回の記事の続きになります。


時間割引関数とは?
時間割引関数は, 時間の経過に応じて価値が目減りする様子を関数化したものになります。
時間割引関数のグラフを書くと,
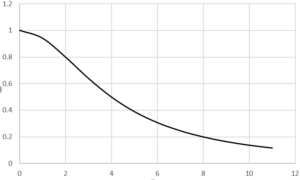

図1.時間割引関数、縦軸:価値の目減り具合\(D(t)\)、横軸:時間\(t\)
このようになります。
時間を\(t\),\(k,q\)は定数とすると,時間割引関数を\(D(t)\)は,
$$D(t)=\frac{1}{(1+k(1-q)t)^{\frac{1}{1-q}}}\tag{1}$$
となります。
時間割引関数は, 指数割引関数と双曲線割引関数に分けられています。
時間割引率とは?
まず,割引率は, 時間\(t\)から時間\(t+\Delta t\)の間にどれだけ価値が目減りしたかを表します。
割引率を時間割引関数\(D(t)\)を用いると,
\(割引率=\frac{D(t)-D(t+\Delta t)}{D(t)}\)
と表せます。
つまり,時間割引率は,同じ金額でも,今もらうより将来もらって得る価値の方が低くなる性質と解釈できます。
そして,時間割引率は単位時間の当たりの割引率です。
時間割引率(単位時間当たりの割引率)は,価値の目減り具合を表す指数と定義され,せっかちさを表す値でよく知られています。
これを式に表すと,
\(時間割引率=\frac{\frac{D(t)-D(t+\Delta t)}{\Delta t}}{D(t)}\)
ここで,\(\Delta t \to 0\)とすると,
\(時間割引率=\frac{-D'(t)}{D(t)}\tag{2}\)
となります。
この時間割引率はあとで出てくるので定義を忘れないでください。
時間割引率は, 価値の目減り率を表すので,
時間割引率が高い程「せっかち」, 時間割引率が低い程「我慢強い」性格になります。
指数割引関数
指数割引関数は, 時間割引関数を近似した関数で, 経済学でよく用いられます。
その理由は, 指数割引関数が時間整合性を持つからです。
時間整合性とは, 理にかなった行動を一貫してとり続けることを言います。
指数割引関数をグラフに表すと,
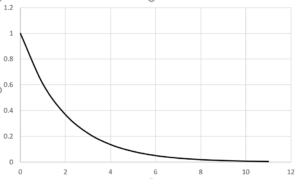
図2.指数割引関数のグラフ、縦軸:価値の目減り率\(D(t)\)、横軸:時間\(t\)
指数割引関数D(t)は, 時間\(t\)と定数\(k\)を用いて以下のように表されます。
D(t)=e^{-kt}
そして, 指数割引関数の時間割引率\(\frac{-D'(t)}{D(t)}\)は,
\(\frac{-D'(t)}{D(t)}=-\frac{-ke^{-kt}}{e^{-kt}}=k\)
となります。
時間割引率は, 価値の目減り具合を表していたので,
指数割引関数は, どの時間\(t\)でも一定の目減りになります。
つまり,指数割引関数は,行動の一貫性という点で双曲線割引関数よりも優れているということになります。
ちなみに,式(1)の時間割引関数は,
$$D(t)=\frac{1}{(1+k(1-q)t)^{\frac{1}{1^q}}}$$
で表せていましたが,定数\(q \to 1\)とすれば,指数割引関数になります。
<証>
\(D(t)\)に極限を取ると,
\(\lim_{q \to 1} D(t)=\frac{1}{(1+k(1-q)t)^{\frac{1}{kt}\frac{1}{1-q}kt}\)
となります。
\(x=\frac{1}{k(1-q)t}\)とおくと,
\(\lim_{q \to 1} D(t)=\lim_{x \to \infty}D(t)=\frac{1}{(1+\frac{1}{x})^{x kt} \)
ここで,極限の公式\(\lim_{x \to \infty} (1+\frac{1}{x})^{x}=e\)より,
\(\lim_{q \to 1} D(t)=\frac{1}{e^{kt}}=e^{-kt}\)
となり,指数割引関数を導けました。
\(D(t)=e^{-kt}\)
<終>
双曲線割引関数
双曲線割引関数は, 指数割引関数よりも実際の時間割引関数に近い近似関数です。
グラフするとこんな感じになります。
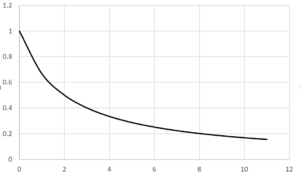
図3.双曲線割引関数のグラフ、縦軸:価値の目減り率\(D(t)\)、横軸:時間\(t\)
時間\(t\),定数\(k\)とすると,双曲線割引関数を\(D(t)\)は,
\(D(t)=\frac{1}{1+kt}\)
となります。更に時間割引率\(\frac{-D'(t)}{D(t)}\)は,
\(\frac{-D'(t)}{D(t)}=\frac{k}{1+kt}\)
となります。
時間割引率\(\frac{-D'(t)}{D(t)}\)は,時間\(t\)が大きいほど低くなります。
この双曲線割引関数の時間割引率によれば,人は,将来の異時間選択に比べると,現在の異時間選択は,より衝動的になることがわかります。
まず,時間割引関数は,現在の1万円と将来の1万円は現在の1万円の方が価値は高いということを前提としています。
これは,現在価値の話でもしましたね。


では,これらの前提を踏まえて,2つの質問をします。
まず,1つ目の質問
あなたは今すぐ1万円が欲しいですか?それとも,1年後に1万2000円が欲しいですか?
時間割引率が高い人は,目先の1万円を選びます。逆に,時間割引率が低い人は,1年後の1万2000円を選びます。
では,2つ目の質問です。
あなたは,9年後に1万円が欲しいですか?それとも,10年後に1万2000円が欲しいですか?
もしかしたら,1つめの質問で,「今すぐ1万円を欲しい」を選択した人も,この質問では,10年後の1万2000円が欲しいを選択したかもしれません。
2つ目の質問をされた時は,1つ目の質問と異なり,2つの選択肢が現在から遠くにある為,金額だけに焦点を当てて意思決定を行ったと思います。
ちなみに,最初の時間割引関数は,
\(D(t)=\frac{1}{(1+k(1-q)t)^{\frac{1}{1-q}}}\)
であり,\(q=0\)とすると,双曲線割引関数になります。
$$D(t)=\frac{1}{1+kt}$$
時間割引関数の特徴
時間割引関数は,どんな特徴があるのでしょうか?
指数割引関数,双曲線割引関数の特徴をそれぞれ見ていきましょう。
| \(D(t)\) | 特徴 | |
| 指数割引関数 | D(t)=\(D(t)=e^{-kt}\) | 選考の逆転現象が起こらない。 |
| 双曲線割引関数 | \(D(t)=\frac{1}{1+kt}\) | 一般人の割引関数に近いが,選考の逆転現象が起こってしまう。 |
経済学の時間割引関数のモデルとしては,指数割引関数の方が良く使われています。
なぜ,双曲線割引関数を使わないのでしょうか?
その答えは,指数割引関数が選考の逆転現象が起こらないことに関係しています。
選考の逆転現象
選考の逆転現象は,私たちの身の回りでも起こる現象です。
選考の逆転現象の2つの具体例を紹介します。
1つは,松竹梅の法則です。
松竹梅の法則は,「3つの選択肢がある場合は真ん中を選ぶ」という行動心理です。
スマホやパソコンのセールスの人が,よく使っているテクニックです。
松竹梅の法則は,フレーミング効果の一種としても知られています。


もう1つは,将来の利益より目先の利益を優先してしまう現象です。
この現象は,双曲線割引関数で起こりますが,指数割引関数では起こりません。
指数割引関数で選考の逆転現象が起こらない理由は,指数割引関数の時間割引率\(-\frac{D'(t)}{D(t)}\)が一定だからです。
\(-\frac{D'(t)}{D(t)}=-k\)
指数割引関数は時間整合性があるので、指数割引関数を使ったモデルは、合理的な選択を取り続ける人のモデルになります。
最後に
時間割引関数は我慢強さを表します。実は,この我慢強さは,知性が高い人ほど,我慢強い性格にあることが知られています。
知性の高さは,皆さんがよく知るIQで表されています。IQは,一般的に学歴に比例しており,これはくつがえすことのできない事実となっています。
我慢強さを手に入れる為に,日頃から勉強しましょう。

















