$$\require{\cancel}$$
今ですか?1週間まで待てますか?1ヶ月まで待てますか?それとも,1年まで待てますか? 私は今なんだよ!
この記事を読んだとき,あなたは,私の質問の真意に気づくことになるでしょう。
この記事を読むと得られる効用
1.事業投資の評価ができます
2.今すぐ,お金を欲しくなります
3.投資がしたくなります
4.年金?思ったより価値ないよ!
今の1万円と1年後の1万円は同じ価値ではない
今の1万円と1年後の1万円は,違います。
理由は2つあります。
理由1:お金は時間によって,価値が変わるから。
え,そんなことあるの?と思うかもしれませんが,あります。
2019年10月に消費税が8%から10増税されましたね。これによって,1万円の価値は下がりました。わからない人の為に例題で説明します。
例題1:
増税前の値段が108[円/個]の商品があるとします。増税後の値段は110[円/個]になります。さて,現金1万円を持っていたとして,増税前と増税後でその商品はそれぞれ何個買えたでしょう。
例題1答え:
増税前:10,000円÷108円/個≒92.6個
増税後:10,000円÷110円/個=90.9個
増税前は,1万円で商品を92個も買えたのに,増税後は,1万円で商品を90個しか買えなくなった。
増税がものの値段を上げたわけですから, お金は時間によって価値が変わるといえます。
では,今度は仮に,ものの値段が時間によらず一定だとしましょう。
それでも,今もらう1万円と将来にもらう1万円の価値は違います。その理由が理由2です。
理由2:お金を使うと利回りが発生するから
利回りとは,お金を使った金額に対する収益の割合のことを意味します。$$利回り=\frac{収益}{お金を使った金額}÷運用年数$$
例えば,1万円を年利1%の銀行に預金すると,下の図のようになります。
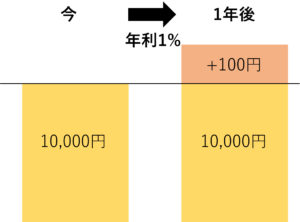
今,1万円をもらうと,1年後には10100円になるので,今の1万円は,1年後の10100円と同じ価値だといえます。よって,1年後の1万円は,今の1万円と同じ価値になりません。
現在価値とは
現在価値は,複利の兄弟です。
言ってる意味がわからないと思いますので,現在価値の定義式を見ましょう。
$$現在価値=\frac{N年後の将来価値}{(1+利子率)^N}$$
この式の両辺を\((1+利子率)^N\)倍してあげると,
$$現在価値(1+利子率)^N=N年後の将来価値$$
この式は複利の式と,等しくなります。
$$元本\times (1+利子率)^N=N年後の金額の合計$$
現在価値\(\Rightarrow\)元本, \(N\)年後の将来価値\(\Rightarrow\)\(N\)年後の金額の合計とすれば,複利の計算式になります。
つまり,現在価値は, \(N\)年後に得たお金を元本として,\(-N\)年間複利運用したものの価値と言い直すこともできます。
例えば,利子率10%で,1年後の将来価値が110万円の物は,現在価値は100万円です。
これは,110万円を元本として,-1年間複利運用したと考えると
現在価値=\(110万円\times(1+N)^{-1}=100万円\)
となります。
年金の現在価値
では,年金の現在価値を求めてみましょう。年金は,退職後に毎年一定額もらえるお金のことです。
例題2:
今年から年金100万円を20年間受け取る場合,もらえる年金の合計と,現在価値を求めましょう。ただし,利子率(年利)は3%とします。
ちなみに年金の平均は,男性が「月額18万円」,女性が「月額9万円」です。(2018年時点)
例題2答え:
もらえる年金の合計は
\(100万円\times 20=2000万円\tag{1}\)
現在価値は,
\(現在価値=100万円\frac{1}{1+0.03}+100万円\frac{1}{(1+0.03)^2}+100万円\frac{1}{(1+0.03)^3}
\)
\(+\cdots+100万円\frac{1}{(1+0.03)^{19}}+100万円\frac{1}{(1+0.03)^{20}}\)
ここで,両辺を1+0.03倍すると,
\(現在価値\times(1+0.03)=100万円+100万円\frac{1}{1+0.03}+100万円\frac{1}{(1+0.03)^2}\)
\(+\cdots+100万円\frac{1}{(1+0.03)^{19}}\tag{2}\)
式(1)-式(2)を行うと,
\(現在価値\times 0.03=100万円-100万円\frac{1}{(1+0.03)^{20}}\)
よって,現在価値は,
\(現在価値=\frac{100}{0.03}(1-\frac{1}{{(1+0.03)^{20}}})≒1487万円\)
年金は,私たちが思っているより価値がないということがわかりました。
このように,現在価値は,自分の利回りを設定することで,将来の資産価値を現在の資産価値に直して計算することが出来るのです。

まとめ
1.複利の計算式->
$$元本\times (1+利子率)^N=N年後の金額の合計$$
2.現在価値の計算方法->
$$現在価値=\frac{N年後の将来価値}{(1+利子率)^N}$$
3.年金は思っているより価値がない
/box03]
最後に
年金は,価値がないわけではありません。長生きというリスクを負ったときの為のリスク分散ツールが年金なのです。本記事は,年金に価値がないかのような言い回しをしていますが,そんなことは無いです。
参考サイトー>


















