$$\require{\cancel}$$
この記事を読むメリット
☑二項モデルを知ることができる
☑二項モデルに基づくコール・オプション価格の計算をできるようになる。
二項モデルとは?
二項モデルは,各期間の価格の変動がアップとダウンで表されるという簡単なモデルです。
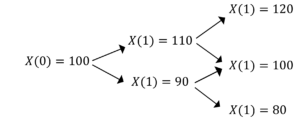
このように,二項モデルを使うと,マクロな価格変動を表すことができます。
二項モデルを更に,簡素化したものはランダムウォークと呼ばれていて,このような図で表されます。
ランダムウォークは二項モデルに対して,ミクロな価格変動を表すことができ,実際の株価の変動と遜色ないので,結構便利です。
二項モデルは,ランダムウォークのように小回りは利かないですが,投資や事業の意思決定を行うときに使えるモデルなのでご紹介します。
二項モデルに基づくコール・オプション価格の決定
二項モデルを使うと,裁定取引が起こらない場合のコール・オプション価格を決定することができます。
ん?難しすぎて何言っているか分からない?
裁定取引:2つの金融商品\(A,B\)の価格差を利用した取引。金融商品\(A\)を買い,金融商品\(B\)を売る取引なので,実質,資金0円で利益を得ることができる取引です。「サヤ取り」とも呼ばれます。
コール・オプション(Call Option):ある日時に,ある物(=原資産)を買う権利のことをいいます。
では,二項モデルに関する問題を解いていきます。
二項モデルを使ったコール・オプション価格の決定例題
さっそく,問題です。
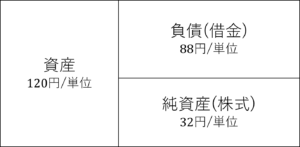
零細企業\(Cupuasu\)は,クーポンレート(年利)10%の利付債を発行して,事業資産\(A\)に投資をするだけの企業です。零細企業\(Cupuasu\)の時刻1での負債総額は,\(88\)になる見込みです。負債総額の内,利子は8です。
事業資産\(A\)は,時刻0に\(x(0)=100\)で取引されています。時刻1にコール・オプション価格がどうなるか予測せよ!ただし,資産\(A\)は,時刻1には,確率\(p\)で\(x(1)=120円\)になり,確率\(1-p\)で\(x(1)=80\)となります。
また,満期1年,額面\(B(1)=100\)の割引債が\(B(0)=90\)で取引されています。
※企業価値保存の法則:\(\underbrace{S}_{株式(純資産)}+\underbrace{D}_{負債(借金)}=\underbrace{V}_{資産}\)が成立
※理想的な証券市場
※裁定取引を行う機会がない!
※倒産コストは0円
このとき,以下の問に答えなさい。
(1) 事業資産\(A\)が120になったとき,時刻1における零細企業\(Cupuasu\)の株式(純資産,資本)\(S(1)\),負債総額\(D(1)\),資産\(V(1)\)を求めよ。
(2) 事業資産\(A\)が80になったとき,時刻1における零細企業\(Cupuasu\)の株式(純資産,資本)\(S(1)\),負債総額\(D(1)\),資産\(V(1)\)を求めよ。
(3) 裁定機会がない場合,時刻0における零細企業\(Cupuasu\)の株式(純資産,資本)\(S(0)\),負債総額\(D(0)\),資産\(V(0)\)を求めよ。
(4) \(p=0.8\)のとき,事業資産\(A\)の期待収益率\(μ_A\)を計算せよ!
(5) \(p=0.8\)のとき,零細企業\(Cupuasu\)の株式の期待収益率\(R_S\),負債の期待収益率\(R_D\)を計算せよ!
(1)解答
事業資産\(A\)が120より,資産\(V(1)\)は,
$$V(1)=120$$
負債総額\(D(1)\)は,題意より
$$D(1)=88$$
株式\(S(1)\)は,企業価値保存の法則より,
$$S(1)=V(1)-D(1)=120-88=32$$
(2)解答
事業資産\(A\)は80なので,資産\(V(1)\)は,
$$V(1)=80$$
となります。負債総額\(D(1)\)は,本来は88ですが,資産\(V(1)\)を超えることはできないので,
$$D(1)=80$$
となります。
また,株式\(S(1)\)は,企業価値保存の法則から,
$$S(1)=0$$
となり,企業は倒産します。

(3)解答
この問題は,複製ポートフォリオを用いて解きます。
事業資産\(A\)と割引債へ分散投資を行う複合ポートフォリオを\(\theta\)とし,時刻\(t\)における複合ポートフォリオの価値を\(\theta(t)\)とします。
複合ポートフォリオは,事業資産\(A\)を\(a\)単位保有し,割引債を\(b\)単位だけ保有します。
すると,\(\theta(0)\),\(\theta(1)\)は次のように書けます。
\(\theta(0)=100a+90b\)
\(\left \{\begin{array}{ccc}\theta(1)=120a+100b\\\theta(1)=80a+100b\end{array}\right.\)
株式と複合ポートフォリオについて考えると,裁定機会は存在しないので,
$$\left \{ \begin{array}{ccc}\theta(1)=S(1)\\ \theta(0)=S(0)\end{array}\right.$$
を満たす複合ポートフォリオは存在します。
よって,
\(\left \{\begin{array}{ccc}120a+100b=32 \\ \theta(2)=80a+100b =0\end{array}\right.\)
の連立方程式が成立します。\(a,b\)について解くと,\(a=0.8,b=-0.64\)となります。
よって,株式\(S(0)\)は,
$$S(0)=100a+90b=100・0.8+90・(-0.64)=23.4$$
となります。
次に,負債総額と複合ポートフォリオについて考えると,裁定機会は存在しないので,
$$\left \{ \begin{array}{ccc}\theta(1)=S(1)\\ \theta(0)=S(0)\end{array}\right.$$
を満たす複合ポートフォリオは存在します。
よって,
\(\left \{\begin{array}{ccc}120a+100b=88 \\ \theta(2)=80a+100b =80\end{array}\right.\)
の連立方程式が成立します。\(a,b\)について解くと,\(a=0.2,b=0.64\)となります。
よって,負債総額\(D(0)\)は,
$$D(0)=100a+90b=100・0.2+90・0.64=77.6$$
となります。
資産\(V(0)\)については,
$$V(0)=S(0)+D(0)=100$$
が成立しています。
(4)解答
事業資産\(A\)の期待収益率\(μ_A\)は,確率\(p\)を用いると,
$$μ_A=\frac{120p-80(1-p)-100}{100}=12%$$
(5)解答
株式の期待収益率\(R_S\)は,確率\(p\)を用いると,\(R_S\)は,
$$R_S=\frac{32p+0(1-p)-23.4}{23.4}$$
より,
$$R_S=\frac{32・0.8-23.4}{23.4}≒9.4%$$
となります。
負債の期待収益率\(R_D\)は,
$$R_D=\frac{88p+80(1-p)-77.6}{77.6}$$
より,
$$R_D=\frac{88・0.8+80・0.2-77.6}{77.6}≒11.3%$$
となります。
まとめると,\(μ_A=12%,R_S=9.4%,R_D=11.3%\)
となり,零細企業\(Cupuasu\)が発行する株式や債券よりも,事業資産\(A\)に直接投資をした方が良さそうです。
複合ポートフォリオが株式や負債総額と一致する理由
問題を真面目に解いた人は,もしかしたら私のように疑問を持った方もいるかと思うので,補足説明をしておきます。
例題の解答例には,裁定機会が存在しないときに,任意に組み合わせた複合ポートフォリオ\(\theta\)が,株式\(S\)や負債総額\(D\)と一致すると書いてありました。
どうして,複合ポートフォリオは,株式や負債総額と一致するのでしょうか?
ここでポイントは,裁定機会が存在しないという点に着目することです。
では,仮に,株式\(\theta(0)>S(0)\)としましょう。
すると,裁定取引が可能になり,
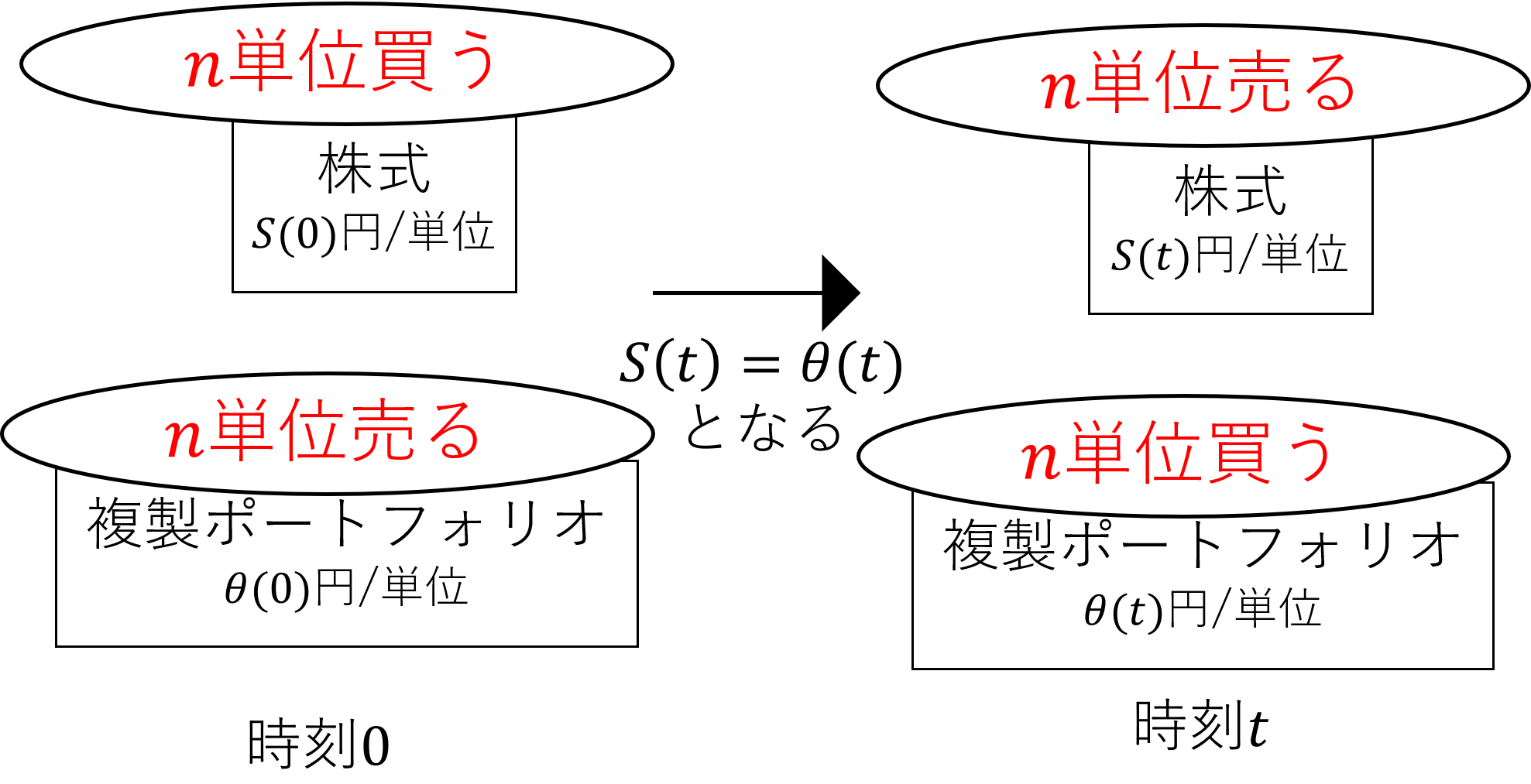
図のように,時刻0で株式を買い,複合ポートフォリオを売った後,\(S(t)=\theta(t)\)時刻\(t\)で株式を売り戻し,複合ポートフォリオを買い戻してしまえば,
\(n[\theta(0)-S(0)]\)円の利益を、資金0で手に入れることができてしまいます。
つまり,裁定機会が存在しない事は,複合ポートフォリオが株式や負債総額と一致する事と必要十分条件であるということです。
二項モデル|まとめ
・二項モデルは,マクロな期間での価格変動を表すことができる
・裁定機会が存在しないとき,複合ポートフォリオは,日経平均株価,TOPIX,ニューヨークダウ平均と一致させることができる
最後に
\(\cancel{私は,二項モデルよりもグラビアモデルの方が好きです。}\)
そもそも,どうして私が投資に興味を持ったのかというと,トマ・ピケティの\(r>g\)の法則を知っているからなんですね。
\(r\)は,投資の利回りで\(g\)は労働による利回りですね。
資金が小さい内は,\(r<g\)となりますが,資金が大きくなる,\(r>g\)となり,投資による利回りが労働による利回りを上回ります。
実際,世界の大富豪であるウォーレン・バフェットや孫正義さんは,投資をしています。
私は,ランダムウォークとマーチンゲール法を使った順張り投資戦術を考えています。ランダムウォーク+確率論を使うことで,マーチンゲール法のシミュレーションが可能になります。
投資をするために,こんなに数学を使うのかと思われるかもしれませんが,
投資の世界では資産=0はゲームオーバーです。
それに,市場はプロが9割です。勝つ為の投資は不可能に近いので,負けない為の投資戦術を理論に基づいて構築する必要があります。
ゲームオーバーにならない為に,堅実に資産を増やしていきます。