皆さんは,プロスペクト理論をご存じでしょうか?このプロスペクト理論は,投資やマーケティングに応用されています。今日は,そんなプロスペクト理論に関するお話です。
今日の記事は,アノマリーの記事の続きになります。

この記事を読むメリット
☑プロスペクト理論とは?
☑価値関数と確率加重関数についてわかる
☑身近な問題をプロスペクト理論で分析
プロスペクト理論とは?
プロスペクト理論は,人間の意思決定及び行動を説明するための理論として知られています。
人間の意思決定や行動には,非合理的な行動が多いですよね?
具体例を2つ程挙げると,
例えば、小学生,中学生であれば,下校中に買い食いします。
しかし,買い食いをすると,栄養バランスが偏ってしまい一般的には身体に良くないと言われています。
また,楽をして大金を稼ごうとするサラリーマン(大学生)は,宝くじやギャンブルをします。(私はしてませんよ。)
宝くじ・ギャンブルは,還元率や期待値を計算すると損することは確定しています。
中には,ボロ勝ちする人もいるでしょうが,それは全体のごく一部です。

下校中の買い食いやギャンブルは非合理的な行動に分類され,このような非合理的な行動は古典経済学では説明ませんが,
プロスペクト理論では,人が非合理的な行動をとる理由を突き止めることができます。
プロスペクト理論では,2つの関数が使われます。
・価値関数
・確率加重関数
この2つの関数について軽く説明した後,実際にプロスペクト理論を使って分析を行っていきます。
価値関数・確率加重関数とは?
価値関数
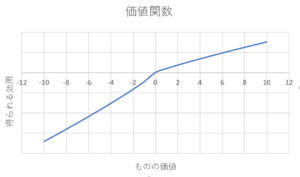
価値関数は,別名:効用関数と呼ばれ,ミクロ経済学などの学問で登場する関数です。
この価値関数は,人間が実際の価値をどのように感じるのかを表したものになります。
実際の価値を\(x\),価値関数を\(v(x)\)とすると次のように表されます。
$$v(x)=\left\{
\begin{array}{ccc}
x^{\alpha}\\
-λ(-x)^{\beta}
\end{array}
\right.$$
\(0<\alpha<1,0<\beta<1,λ>1\)
価値関数の特徴は,
1. 得したいという欲求よりも損失の恐怖の方が強い
2. もらえる金額が2倍になっても,嬉しさが2倍になるわけではない
価値関数について,詳しくは下の記事をご覧ください。
確率加重関数
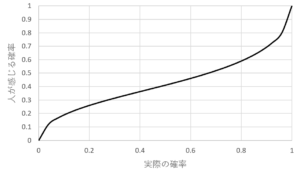
確率加重関数は,人が確率の錯覚する現象を関数化したものです。
実際の確率を\(p\),確率加重関数を\(w(p)\)とすると,
$$w(p)=\frac{p^γ}{(p^γ+(1-p)^γ)^{\frac{1}{γ}}}$$
と表せます。
確率加重関数の特徴は,
1. 低い確率を実際より高く評価する
2. 高い確率を実際より低く評価する
確率加重関数について,詳しくは下の記事をご覧ください。
身近な問題をプロスペクト理論で分析
今回の分析に用いる宝くじは,ナンバーズ4です。
ナンバーズ4は,4桁の数字を当てると当選金額90万円もらえるシンプルな宝くじとなっております。
詳しくは,こちらの記事をご参照ください。

宝くじの期待値を計算
プロスペクト理論で分析する前に,宝くじの期待値を計算しておきます。
| 確率 | 当選金額 | |
| 4桁の数字を当てる | \(\frac{1}{10000}\) | 90万円 |
| 4桁の数字をはずす | \(\frac{9999}{10000}\) | 0万円 |
上の表から,宝くじを一枚買ったときにもらえる金額の期待値\(m\)は,
\(m=\underbrace{\frac{1}{10000}×90万円}_{4桁の数字を当てる}+\underbrace{\frac{9999}{10000}}_{4桁の数字をはずす}-200円=-110円\)
となります。
この結果から,宝くじ(ナンバーズ4)を一枚買うと平均110円損することがわかりました。
平均で110円損するのに,なぜ宝くじを買う人がいるのでしょうか?
これは,プロスペクト理論の価値関数と確率加重関数を使って計算するとわかります。
宝くじ(ナンバーズ4)をプロスペクト理論で分析

宝くじの問題をプロスペクト理論の価値関数と確率加重関数を用いて分析していきましょう。
| 確率 | 当選金額 | |
| 4桁の数字を当てる | \(w(\frac{1}{10000})=0.00433\) | \(v(90万円)=173673\) |
| 4桁の数字をはずす | \(w(\frac{9999}{10000})=0.99269\) | \(v(0万円)=0\) |
上の表から,宝くじを1枚買ったときに人が感じる期待値\(m’\)は,
\(m’=w(\frac{1}{10000})×v(90万円)+w(\frac{9999}{10000})×v(0万円)+v(-200円)\)
\(m’=0.00433×173673+(-238.3)≒+514\)
+514となりました。
なんと,宝くじ(ナンバーズ4)一枚で人間が感じる期待効用は+514となるみたいです。
宝くじ一枚当たり平均で110円の損失があるにもかかわらず,+514のプラスの効用を感じます。
損をするのに喜びを感じることが宝くじや保険の恐ろしさです。
プロスペクト理論でフレーミング効果を説明

皆さんは,フレーミング効果をご存じですか?
フレーミング効果(framing effect)は,同じ選択肢であっても,表現の方法や状況に応じて選択を変える効果のことを言います。
詳しくは,下記の記事を読んでください。

実は,このフレーミング効果もプロスペクト理論を使うと少しだけ説明できます。(フレーミング効果の全てを説明できるわけではない)
質問1.あなたは次の2つ選択肢のうち1つだけ選ぶことができます。
1) 100%の確率で1万円もらえる賭け事
2) 10%の確率で10万円もらえるが,残りの90%の確率で何ももらえない賭け事
どちらを選ぶ?
質問1を受けると,多くの人は1)を選択します。
価値関数を使って説明すると,
2つの選択肢を見た場合,価値関数の参照点が左に1万円分移動します。
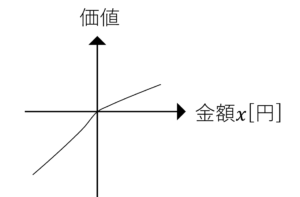
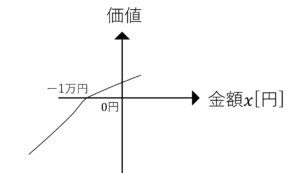

図1.価値関数(左),参照点が左に1万円ズレた価値関数(右)
このギャンブルを行う前の時点で,得られる効用が既にプラスなるので,更なる利益を求めるよりもリスクを避けた行動を取るようになります。
この行動原理のことを「リスク回避的」といいます。
質問2は,具体例1と反対のことを書いています。
質問2.あなたは次の2つ選択肢のうち1つだけ選ぶことができます。
1) 100%の確率で1万円を失う賭け事
2) 10%の確率で10万円を失うが,残りの90%の確率で何も失わない賭け事
どちらを選ぶ?
質問2の場合は,2)を選ぶ人の割合が多くなります。
価値関数を用いて説明すると,
価値関数の参照点が右に1万円分移動します。



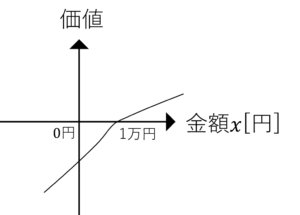

図2.価値関数(左),参照点が右に1万円ズレた価値関数(右)
すると,この時点で効用が既にマイナスなので,これ以上の損失が怖くなくなります。
よって,10万円失うリスクを負ってでも,何も失わない方の選択肢を選ぶようになります。
このような行動原理を「リスク愛好的」といいます。
人が合理的な行動を取るとしたら,一貫した行動をとります。
例えば,「リスク愛好型」の人は,質問1と質問2で2) を選択し続け,「リスク回避型」の人は,質問1と質問2で1) を選択し続けます。
フレーミング効果は,「リスク中立型」の人達の周りの状況に応じて,「リスク愛好的」な選択をしたり「リスク回避的」な選択をしたりする現象を説明したものになります。
プロスペクト理論:まとめ
プロスペクト理論のまとめです。
・プロスペクト理論は,価値関数と確率加重関数を使う
・宝くじや保険は損をするのに喜びを感じる
・フレーミング効果は状況に応じて選択を変える心理効果
宝くじや保険をするくらいなら,資産運用(投資)をすることをオススメします。
資産運用(投資)の世界は,還元率が100%を超えた世界です。
つまり、投資に参入すれば理論上,平均的に勝ち続けることができます。
資産運用についてまとめた記事はこちらです。


投資初心者が陥りやすい罠について解説した記事がこちらになります。


最後に
経済学は,数学を通して体系的に理解することができます。
行動経済学ももちろん例外ではありません。
私はこれから,マーケティング・投資で勝つ為に,経済学・数学を勉強していきます。



















