この記事を読むメリット
☑人が確率をどのように錯覚するのかがわかる
☑人が確率を錯覚する原理を利用して行動を予測できる
☑ポケモンの技の命中率30%=命中率70%の原理がわかる
プロスペクト理論|確率加重関数とは?


確率加重関数は,\(w(p)\)と表され,人が感じる主観的な確率になります。
人は実際の確率\(p\)を,確率\(w(p)\)と錯覚します。
では,\(w(p)\)はどのように表されているのでしょうか?
グラフに書くとこんな感じです。
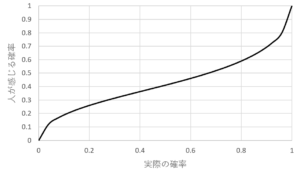

図1.\(γ=0.59\)のときの確率加重関数
確率加重関数\(w(p)\)は,Tversky&Kahnemanが提案した関数が有名で,確率\(p\)と定数\(γ\)を用いて表されます。
$$w(p)=\frac{p^{γ}}{(p^γ+(1-p)^γ)^{\frac{1}{γ}}}$$
では、確率加重関数\(w(p)\)から人がどのように確率を錯覚するのか詳しく見ていきましょう。
確率加重関数の特徴


グラフから,次のことが読み取れます。
1. 実際の確率が低いと確率を過大評価する
2. 実際の確率が高いと確率を過小評価する
3. 確率が0,1付近では,確率値の差には敏感になる
実際の確率が低いと確率を過大評価する
人は,客観的確率(実際の確率)が低いときは,主観的な確率(人が認識する確率)を高く見積もる傾向があります。
例えば,宝くじの購入や保険の加入などが良い例です。
宝くじは,当たりそうで当たりませんよね?
これは,確率加重関数から見た宝くじを買う人全ての心理状態になります。
保険は,万が一のリスク(予期せぬ事故やトラブル)への備えとして,保険会社に保険料を支払うものですが,
万が一のリスクは,宝くじに当選するのと同じように簡単には起こりません。だから,保険は「不幸の宝くじ」と呼ばれています。
実際の確率が高いと確率を過小評価する
人は,客観的確率(実際の確率)が高いときは,主観的な確率(人が認識する確率)を低く見る傾向があります。
例えば,ポケモンの技の「じゃれつく」,「がんせきふうじ」,「こごえるかぜ」などは,思った以上に外れませんか?
これは,確率加重関数による錯覚で,外した回数と技を使った回数を数えてみると,ポケモンの技の命中率に近づきます。
確率が0,1付近では,確率値の差には敏感になる

それでは,私の実体験に基づいた,確率加重関数による対話文を挙げましょう。
確率30%~70%はあまり当てにならない数字ですよね?
なぜなら,予想をくつがえったとしても納得できる確率だからです。
人はどっちつかずな確率を認知しづらいということです。
私が降水確率70%くらいでも傘はもっていかないのはまた別の話ですけれどもね。
確率加重関数を使った消費者の心理分析


確率加重関数を使って,実際に宝くじを買う人の心理状態を分析していこうと思います。
検証に用いる宝くじは,還元率45%の「ナンバーズ4」という宝くじになります。
ナンバーズ4は,1枚当たり購入金額は200円くらいで,4桁の数字を当てると90万円がもらえるシンプルな宝くじになっております。
詳しくは,下の記事を読んでください。


宝くじの期待値を計算
いきなり確率加重関数を使うと,混乱すると思うので,普通の確率を用いて計算します。
| 確率 | 当選金額 | |
| 4桁の数字を当てる | \(\frac{1}{10000}\) | 90万円 |
| 4桁の数字をはずす | \(\frac{9999}{10000}\) | 0万円 |
上の表から,宝くじを一枚買ったときにもらえる金額の期待値\(m\)は,
\(m=\underbrace{\frac{1}{10000}×90万円}_{4桁の数字を当てる}+\underbrace{\frac{9999}{10000}}_{4桁の数字をはずす}-200円=-110円\)
となります。
この結果から,宝くじ(ナンバーズ4)を一枚買うと平均110円損することがわかりました。
残念です。
しかし,平均110円損しても買いたいという人はいますが一体なぜでしょうか?
これは,確率加重関数を使って期待値を計算すると上手く説明ができます。
確率加重関数を使った期待値計算


次に,確率加重関数を用いて,期待値を計算します。
確率加重関数\(w(p)\)を使って計算すると,私達が体感する客観的期待値が求まります。
| 確率 | 当選金額 | |
| 4桁の数字を当てる | \(w(\frac{1}{10000})=0.00433\) | 90万円 |
| 4桁の数字をはずす | \(w(\frac{9999}{10000})=0.99269\) | 0万円 |
上の表から,宝くじを1枚買ったときに人が感じる期待値\(m”\)は,
\(w(\frac{1}{10000})×90万円+w(\frac{9999}{10000})×0万円-200円=0.00433×90万円-200円=+3700円\)
ん?+3700円?
\(γ=0.59\)の確率加重関数によると,人は宝くじを買うと平均的に3,700円くらい儲かると感じるみたいです。
もちろん,人が感じる期待値は間違っていて,実際の期待値は,-110円となります。
そりゃあ,宝くじを買いたがるわけです。
おまけ:価値関数(効用関数)
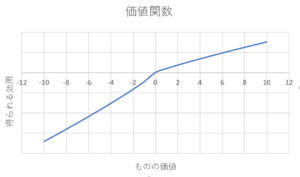

プロスペクト理論は,確率加重関数と価値関数(効用関数)で構成されています。
価値関数は,上のグラフのように,人が実際に感じる価値と実際の価値との間に差があることを意味する関数です。
先ほど紹介した確率加重関数と価値関数を使えば,人の非合理的な行動を説明でき,ギャンブル,投資,マーケティング戦略に応用できます。
詳しくは,
下記の記事をご参照ください。

確率加重関数|まとめ


人の確率を錯覚する原理を理解できたでしょうか?
重要ポイントをまとめると,
・確率が低いと高く見積もる
・確率が高いと低く見積もる
・価値関数と併用すると,人の行動を分析できる
最後に
今まで確率加重関数について見てきましたが,最後にポケモンの技について軽く語りたいと思います。
ポケモンで命中率が低くて強力な技を紹介します。
ポケモンの4大一撃必殺「つのドリル,ハサミギロチン,じわれ,ぜったいれいど」(命中率:30%)。自分が使うとあまり当たらないのに,敵が使うと結構当たる。
それから,「さいみんじゅつ」(命中率:60%)という技も強力ですよね。「じゅうりょく+さいみんじゅつ」で命中率を100%にできるらしいです。
あと,「ねむりごな」(命中率:75%)は,特性を「ふくがん」にすると,ほぼ100%の命中率になります。
ちなみに,ぜったいれいどを英語に直すと,アブソリュートゼロ(absolute 0)となります。