始めました。
今日は,価値関数に関するお話をします。
価値関数とは?

価値関数は、プロスペクト理論に出てくる関数の一種です。
価値関数\(f(x)\),実際の価値を\(x\)とすると,
\(f(x)=\left\{
\begin{array}{ccc}
x^{\alpha}\\
-λ(-x)^{\beta}
\end{array}
\right.
\)
※\(0<\alpha<1,0<\beta<1,λ>1\)
と表されます。
グラフを書くとこんな感じ
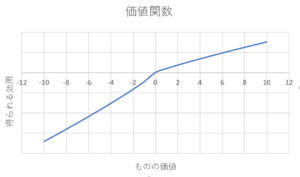
図1.\(\alpha=\beta=0.88,λ=2.25\)
例えば,あなたが1万円を手に入れると\(x=1万円\),体感する価値は\(f(1万円)\)となります。
逆に,あなたが1万円を失うと\(x=-1万円\),体感する価値は\(f(-1万円)\)となります。
価値関数を分析

価値関数の\(\alpha,\beta,λ\)をそれぞれ,0.88,0.88,2.25として計算してみました。
\(x\)が―5万円~+5万円の範囲で価値関数\(f(x)\)を計算すると,次のようになりました。
| \(x\) | \(f(x)\) |
| ―5万円 | -30709 |
| ―4万円 | -25235 |
| ―3万円 | -19591 |
| ―2万円 | -13712 |
| ―1万円 | -7450 |
| 0円 | 0 |
| 1万円 | -3311 |
| 2万円 | -6094 |
| 3万円 | -8707 |
| 4万円 | -11215 |
| 5万円 | 13649 |
金額\(|x|\)が2倍になっても,実際に体感する価値\(f(x)\)は,2倍より低くなります。
このことから,価値\(f(x)\)は,金額\(|x|\)が大きくなるにつれて増加率が逓減することがわかります。
また,価値関数\(f(x)\)について,\(\alpha=\beta\)とおくと,
\(f(x)=\left\{
\begin{array}{ccc}
x^{\alpha}\\
-λ(-x)^{\alpha}
\end{array}
\right.\)
となります。このことから,得よりも損失の方がλ培だけ苦痛に感じます。
グラフによると,\(λ=2.25\)より得よりも損失の方が2.2~2.3倍くらい苦痛に感じるということがわかります。
次に,\(x\)円の損失は,何円の利益に相当するのかを計算します。
+の価値関数を\(f_1(x)\),―の価値関数を\(f_2(x)\)と定義すると,
\(f_1(x)=x^{\alpha}\),\(f_2(x)=-λ(-x)^{\alpha}\)とおけます。
\(\underbrace{f_1(x)}_{+の価値関数}+\underbrace{f_2(x)}_{-の価値関数}=0\)とおくと,
\( x^{\alpha}+( -λ(-x)^{\alpha})=0\)
\(x^{\alpha}=λ(-x)^{\alpha}=0\)
よって,
\(\underbrace{x}_{利益}=λ^{\frac{1}{\alpha}}\underbrace{(-x)}_{損}\)
となりました。
このことから,\(x\)円の損失によるショックは,\(λ^{\frac{1}{\alpha}}x\)円の利益による喜びに匹敵するということがわかります。
また,価値関数のグラフによると,\(λ=2.25,\alpha=\beta=0.88\)より,
\(λ^{\frac{1}{\alpha}}=2.25^{\frac{1}{0.88}}=2.51\)
\(x\)円の損失によるショックは,\(2.5x\)円相当の利益による喜びに匹敵する
ということがわかります。
価値関数の特徴

価値関数を数学的に分析した結果以下の事がわかりました。
1. 金額|x|が大きくなるにつれて\(f(x)\)の増加率は次第に低下する
2. 得よりも損失の方が2.2~2.3倍くらい苦痛に感じる
3. \(x\)円の損失によるショックは,\(2.5x\)円相当の利益による喜びに匹敵する
人間は,極度に損失を嫌う傾向があるということがわかりました。
価値関数|応用

価値関数からわかる人間の行動及び陥りやすい心理状態を2つご紹介します。
1. 損失回避性
2. フレーミング効果
損失回避性
損失回避性は,その名前の通り人間が損失を嫌う傾向があることをいいます。
損失回避性に関する具体例を2つ程だします。
具体例1
以下の2つのくじをあなたは選ぶことができます。片方しか選べないとき,どちらのくじを選びますか?
1) 必ず5万円が当たるくじ
2) 1/2の確率で10万円が当たり,1/2の確率で0円のくじ
この場合は,多くの人は「1) 必ず5万円が当たるくじ」を選びます。なぜなら,2)の選択肢を選ぶと1/2の確率で5万円の損失を被るからです。
では,次の例はどうでしょう?
具体例2
1) 必ず5万円の罰金を払わないといけない
2) 1/2の確率で10万円を払わないといけないが,1/2の確率で罰金が0円
このように,先ほどと条件を変えると,「2) 1/2の確率で10万円を払わないといけないが,1/2の確率で罰金が0円」という選択肢を選ぶ人の割合が多くなります。
「リスク志向的」な人は,2)を選び続け,「リスク回避的」な人は,1)を選び続けます。
では,具体例1で1)を選び,具体例2で2)を選んだ人の思考はどうなっているのでしょうか?
実際に計算してみます。
| 具体例1―1)の得られる価値の期待値 | \(1×f(5万円)=13649\) |
| 具体例1―2)の得られる価値の期待値 | \(\frac{1}{2}×f(0円)+\frac{1}{2}×f(10万円)=12559\) |
| 具体例2―1)の得られる価値の期待値 | \(1×f(-5万円)=-30710\) |
| 具体例2―1)の得られる価値の期待値 | \(\frac{1}{2}×f(0万円)+\frac{1}{2}×f(-10万円)=-28259\) |
このように,価値関数の期待値を計算することによって,人間が持つ損失回避性をうまく説明できるというわけです。
フレーミング効果

続いて,フレーミング効果について説明します。
フレーミング効果(framing effect)は,問題や質問のされ方によって意思決定が変わる事をいいます。
あなたは,どちらの手術を受けたいと考えますか?
1) 失敗率10%の手術
2) 成功率90%の手術
この質問は,損失回避性から2)を選ぶ人が多い傾向があります。
フレーミング効果について詳しく知りたい方はこちらの記事へ

価値関数:まとめ

価値関数は,
$$f(x)=\left\{
\begin{array}{ccc}
x^{\alpha}\\
-λ(-x)^{\alpha}
\end{array}
\right.
$$
・人は損失を極度に嫌う
・損失回避性やフレーミング効果の元となっている
最後に
ブログ運営をしていると,価値関数が変わります。先日機材を5000円で購入したのですが,
5000円という大金を出し渋ることなく手放すことに成功しました。
そして,一ヶ月で100円稼いだときの喜びがえげつないです。