[空間ベクトル]s+t+u=1の公式の導出とその応用

ユキ

$s+t+u=1$。どうも，ユキです。今日は，空間ベクトルの有名な公式の覚え方を伝授しようと思います。

この記事を読むメリット

･公式を忘れたとしても，思い出すきっかけを作ります
･実際に公式を問題に応用させることが出来るようになります。

[空間ベクトル]s+t+u=1の公式の導出

三次元空間の点Pは，$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$の3つのベクトルを使って表すことが出来ます。
$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\tag{1}$$

では，点Pが二次元平面OAB上にある場合について考えると
$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\tag{2}$$
このように書きます。平面OAB上に点Pが存在するので，平面OABから出て行く向きの$\overrightarrow{OC}$を$u=0$とすることによって，止めてあげました。

更に，点Pが一次元直線OA上にある場合は
$$\overrightarrow{OP}=s\overrightarrow{OA}\tag{3}$$
と書きます。先ほど同様，直線OAからはみ出すベクトル$\overrightarrow{b}$を止めました。

(1)~(3)の式を並べてみましょう。

一次元
$$\overrightarrow{OP}=s\overrightarrow{OA}\tag{3}$$
二次元
$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\tag{2}$$
三次元
$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\tag{1}$$

このことから，ベクトルの数と次元の数は一致していることがわかります。

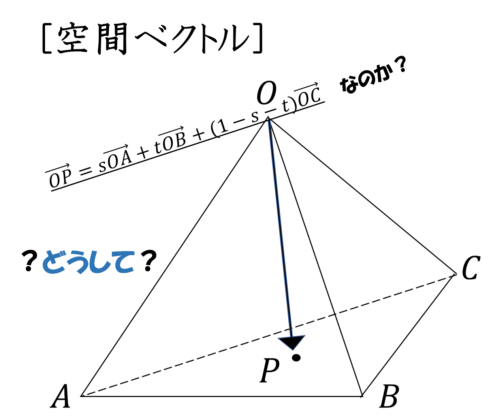
ということは，平面ABCは，二次元なので，平面ABC上の点Pは2つのベクトルで表すことが出来るはずです！

でも，平面ABCを表す点Pの式は，ベクトルが3つあるように見えます。

<div class=”simple-box3″><p>$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\tag{4}$$
ただし，$s+t+u=1$</p></div>

$s+t+u=1$の制約がどうも怪しいですね。

では，平面ABC上の点Pを2つのベクトルで表してみましょう。

平面ABC上の点Pを表すベクトル$\overrightarrow{OP}$の導出

平面ABC上の点Pを2つのベクトルで表すと，

$$\overrightarrow{CP}=s\overrightarrow{CA}+t\overrightarrow{CB}$$
です。式(2)のOをCに変えただけです。

この式から，式(4)を導きます。

まず，左辺に$\overrightarrow{OC}$を足します。

(左辺)$= \overrightarrow{OC}+\overrightarrow{CP}=\overrightarrow{OP}$

次に，右辺に$\overrightarrow{OC}$を足します。

(右辺)$=\overrightarrow{OC}+s\overrightarrow{CA}+t\overrightarrow{CB}$

ベクトルの基準をOとすると，

(右辺)$=s(\overrightarrow{OA}-\overrightarrow{OC})+t(\overrightarrow{OB}-\overrightarrow{OC})+\overrightarrow{OC}$

整理すると，

(右辺)$= s\overrightarrow{OA}+t\overrightarrow{OB}+(1-s-t) \overrightarrow{OC}$

となります。

ここで，$1-s-t=u$とすると，$s+t+u=1$が言えて，(左辺=右辺)より

$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+ (1-s-t)\overrightarrow{OC}\tag{4}$$
となって，式(4)が成立します。

<終>

発展1：直線ODと平面ABCで交わる点Pについて

今，私たちはOからPへ向かうベクトルの求め方を2つ学習しました。

1つは，式(4)

$$\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+ (1-s-t)\overrightarrow{OC}\tag{4}$$
もう1つは，式(3)
$$\overrightarrow{OP}=k\overrightarrow{OD}\tag{3}$$
です。

式(3)と式(4)は，どちらも同じベクトルなので，

$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$について係数比較することができます。係数比較をすると，方程式が3つ出てきます。そして，変数も$s，t，k$の3つなので，変数$s，t，k$の値を求めることが可能です。

実際に，大学入試問題でも，ベクトル$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$の係数比較を使った問題は，よく出てきます。