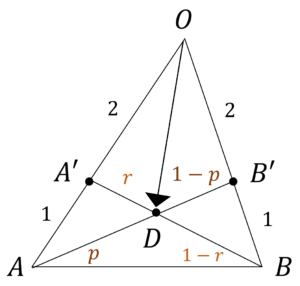今日は,これから大学受験を控える高校生を応援する為に,大学入試数学の問題と解答方法について解説します。今日の記事は,題名にもあるとおり,「空間ベクトル」の問題です。
この記事を読むメリット
☑空間ベクトルの問題を解く練習
問題1
問題1:
四面体OABCを考える。辺OAを1:1に内分する点をPとする。また辺OBを2:1に内分する点をQとして,辺OCを3:1に内分する点をRとする。
さらに三角形ABCの重心をGとする。3点P,Q,Rを通る平面と線分OGの交点をKとする。線分OK とKGの長さの比を求めよ。
問題1解答例
点Kは平面PQRに存在するので,
$$\overrightarrow{OK}=s\overrightarrow{OP}+t\overrightarrow{OQ}+(1-s-t)\overrightarrow{OR}\tag{1}$$
また,点Kは線分OG上にあるので,
$$\overrightarrow{OK}=k\overrightarrow{OG}\tag{2}$$
式(1),式(2)を係数比較して\(k\)を求めます。
\(\overrightarrow{OP},\overrightarrow{OQ},\overrightarrow{OR},\overrightarrow{OG}\)について,題意より
\(\overrightarrow{OP}=\frac{1}{2}\overrightarrow{OA}\)
\(\overrightarrow{OQ}=\frac{2}{3}\overrightarrow{OB}\)
\(\overrightarrow{OR}=\frac{3}{4}\overrightarrow{OC}\)
\(\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}\)
よって,式(1),式(2)は,
$$\overrightarrow{OK}=\frac{1}{2}s\overrightarrow{OA}+\frac{2}{3}t\overrightarrow{OB}+\frac{3}{4}(1-s-t)\overrightarrow{OC}\tag{1’}$$
$$\overrightarrow{OK}=\frac{1}{3}k\overrightarrow{OA}+\frac{1}{3}k\overrightarrow{OB}+\frac{1}{3}k\overrightarrow{OC}\tag{2’}$$
式(1’),式(2’)で係数比較をすると,
\(\overrightarrow{OA}:\frac{1}{2}s=\frac{1}{3}k \Rightarrow s=\frac{2}{3}k\tag{3}\)
\(\overrightarrow{OB}:\frac{2}{3}t=\frac{1}{3}k \Rightarrow t=\frac{1}{2}k\tag{4}\)
\(\overrightarrow{OC}:\frac{3}{4}(1-s-t)\frac{1}{3}k\tag{5}\)
式(3),式(4)を式(5)に代入する
\(\frac{3}{4}(1-\frac{2}{3}k-\frac{1}{2}k)=\frac{1}{3}\)
整理すると,\(k\)は,
\(k=\frac{18}{29}\)
式(2)に代入すると,
$$\overrightarrow{OK}=\frac{18}{29}\overrightarrow{OG}$$
ここで,\(\overrightarrow{KG}=\overrightarrow{OG}-\overrightarrow{OK}\)から,
線分OK とKGの長さの比は,
$$OK:KG=\frac{18}{29}OG:OG-\frac{18}{29}OG$$
よって,線分OKとKGの長さの比は,
$$OK:KG=18:11$$
<終>
問題2
問題2:
四面体OABCを考え,\(\overrightarrow{a}=\overrightarrow{AB},\overrightarrow{b}=\overrightarrow{OB},\overrightarrow{c}=\overrightarrow{OC}\)とする。
また,線分OA,OB,OCを2:1に内分する点をそれぞれA’,B’,C’とし,直線BC’と直線B’Cの交点をD,3点A’,B,Cを通る平面と直線ADの交点をEとする。(1) \(\overrightarrow{OD}\)を\(\overrightarrow{b}\)と\(\overrightarrow{c}\)で表せ
(2) \(\overrightarrow{OE}\)を\(\overrightarrow{a}\),\(\overrightarrow{b}\),\(\overrightarrow{c}\)で表せ。
問題2(1)解答例
\(\overrightarrow{OA’},\overrightarrow{OB’},\overrightarrow{OC’}\)について
\(\overrightarrow{OA’}=\frac{2}{3}\overrightarrow{OA},\overrightarrow{OB’}=\frac{2}{3}\overrightarrow{OB},\overrightarrow{OC’}=\frac{2}{3}\overrightarrow{OC}\)
ここで,図1のようにB’D:DC=\(r\):\(1-r\),BD:DC’=\(p\):\(1-p\)とおくと,
図1.B’D:DC=\(r\):\(1-r\),BD:DC’=\(p\):\(1-p\)としたときの\(\triangle ABC\)
\(\overrightarrow{OD}\)は,2通りの表し方があって,それぞれ
$$\overrightarrow{OD}=(1-r) \overrightarrow{OB’}+r\overrightarrow{OC}=\frac{2}{3}(1-r)\overrightarrow{OB}+r\overrightarrow{OC}\tag{1}$$
$$\overrightarrow{OD}=(1-p)\overrightarrow{OB}+p\overrightarrow{OC’}=(1-p)\overrightarrow{OB}+\frac{2}{3}p\overrightarrow{OC}\tag{2}$$
となります。上の2式を係数比較すると,
\(p=\frac{3}{5}\),\(r=\frac{2}{5}\)
式(1)に\(r\)を代入すると,
\(\overrightarrow{OD}=(1-\frac{2}{5})\frac{2}{3}\overrightarrow{OB}+\frac{2}{5}\overrightarrow{OC}=\frac{2}{5}\overrightarrow{b}+\frac{2}{5}\overrightarrow{c}\)
問題2(2)解答例
点Eは平面A’BC上に存在するので,
$$\overrightarrow{OE}=s\overrightarrow{OA’}+t\overrightarrow{OB}+(1-s-t)\overrightarrow{OC}\tag{3}$$
$$\overrightarrow{OE}=\overrightarrow{OA}+k\overrightarrow{AD}\tag{4}$$
上の2式を係数比較して,\(k\)を求めます。
\(\overrightarrow{OA}\),\(\overrightarrow{AD}\)について
\(\overrightarrow{OA’}=\frac{2}{3}\overrightarrow{OA}\),\(\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}=-\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}+\frac{2}{5}\overrightarrow{OC}\)
よって,2式は,
$$\overrightarrow{OE}=\frac{2}{3}s \overrightarrow{OA}+t \overrightarrow{OB}+(1-s-t) \overrightarrow{OC}\tag{3′}$$
$$\overrightarrow{OE}=(1-k) \overrightarrow{OA}+\frac{2}{5}k \overrightarrow{OB}+\frac{2}{5}k\overrightarrow{OC}\tag{4′}
$$
と書き換えられます。
式(3′)と式(4′)を係数比較をすると,
\(\overrightarrow{OA}:\frac{2}{3}=1-k \Rightarrow s=\frac{3}{2}(1-k)\tag{5}\)
\(\overrightarrow{OB}:t=\frac{2}{5}k\tag{6}\)
\(\overrightarrow{OC}:1-s-t=\frac{2}{5}k\tag{7}\)
式(5),式(6)を式(7)に代入
\(1-\frac{3}{2}(1-k)-\frac{2}{5}k=\frac{2}{5}k\)
式を整理すると,\(k\)は,
\(k=\frac{5}{7}\)
よって,\(k\)を式(4′)に代入すると,
\(\overrightarrow{OE}=\overrightarrow{OA}+\frac{5}{7}\overrightarrow{AD}=\frac{2}{7}\overrightarrow{a}+\frac{2}{7}\overrightarrow{b}+\frac{2}{7}\overrightarrow{c}\)
まとめ
点Pが平面ABC上にある\(\Longleftrightarrow\)
$$\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}+(1-s-t)\overrightarrow{c}$$
点Cが直線AB上にある\(\Longleftrightarrow\)
$$\overrightarrow{AC}=k\overrightarrow{AB}$$
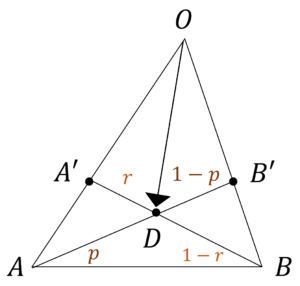 上図のように辺の比を置いて,
上図のように辺の比を置いて,として,係数比較してあげると求まる。
関連問題
問題まとめページー>
https://cupuasu.club/tag/highschool-math/
最後に
空間ベクトルは数学の中でも難しい単元です。頑張って耐えてください。
それでは,引き続き勉強を頑張ってください。