$$\require{\cancel}$$
ちなみに,導関数とは,関数を微分したもので,\(f’(x)\)や,\(\frac{d}{dx}f(x)\)と書いたりします。別にどちらを使っても差し支えありませんが,ここでは,\(f’(x)\)を導関数とします。
微分とは
微分は,平均変化率の進化形です。
平均変化率は,
$$\frac{yの変化量}{xの変化量}=\frac{f(x+h)-f(x)}{(x+h)-x}$$
このように表せます。\(h\)は2点の\(x\)軸方向の距離を表します。平均変化
率は,この\(h\)が,0以外の数でしたが,関数\(f(x)\)の微分は,逆に\(h\)
が0です。式で書くと,
$$\displaystyle \lim_{h \to 0} \frac{f(x+h)-f(x)}{(x+h)-x}$$
このように表せます。ここで,\(\displaystyle \lim_{h \to 0}\)の意味は,\(h\)を0に近づけることを意味します。
つまり,微分の定義は,
$$f’(a)=\displaystyle \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
です。\(f’(a)\)は\(x=a\)における微分係数といいます。
\(x^n\)の微分のやり方
ルールは2つだけです。
$$(x^n)’=n(x^{n-1})\tag{1}$$
$$(c)’=0\tag{2}$$
ここで,\(c\)は,変数\(x\)によらない定数であるとします。
これだけだとわかりづらいので,手順を図に示します。
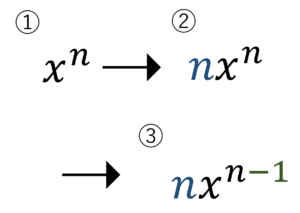
図1.手順に従って微分をやればOKです

例題5問
例題1:\(x^3\)の導関数を求めましょう。
例題1解答:
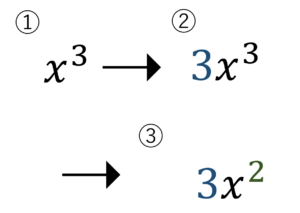
式で書くとこのようになります。
\(f’(x)=(x^3)’=3x^{3-1}=3x^2\)
<終>
次に行きます。
例題2:\(3x^2\)の導関数\(f’(x)\)を求めましょう
例題2解答:
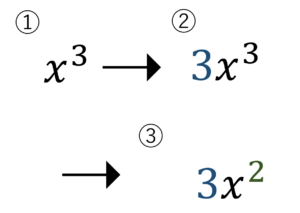
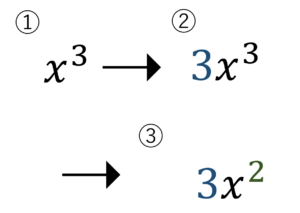
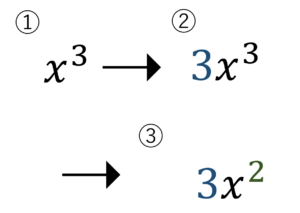
式で書くと,
\(f’(x)=(3x^2)=3・2x^{2-1}=2x\)
<終>
![]()
例題3:\(3c\)の導関数\(f’(x)\)を求めましょう。\(c\)は\(x\)によらない定数。
例題3解答:
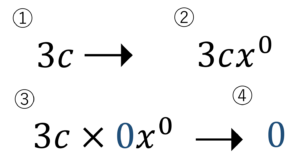
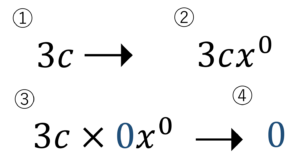
\(f’(x)=(3c)’=(3cx^0)’=0\)
<終>
\(x\)に関して0次式である数は,微分すると,0になります。
例題4:\(\frac{1}{x^3}\)の導関数を求めましょう。ヒント,分数は\(x\)の-3乗
例題4解答:
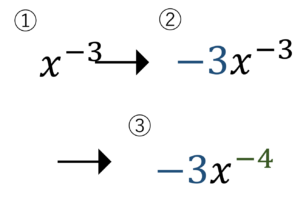
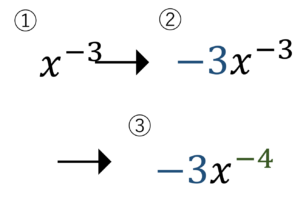
\(f’(x)=\frac{1}{x^3}=x^{-3}=-3x^{-4}\)
<終>
![]()
例題5:\(x^3+\frac{1}{x^3}\)の導関数\(f’(x)\)を求めましょう。
例題5解答:
\(f’(x)=(x^3+x^{-3})’=3x^2-3x{-4}\)
例えば,\(3x^2+6x\)の導関数は,
\((3x^2+6x)’=3(x^2)+6(x)’\)
\(=3・2x+6=6x+6\)
<終>


微分の定義から導関数をもとめるやり方
例題6:\(x^3\)の導関数を微分の定義に従って,もとめましょう。
例題6解答:
微分の定義は,
\(f’(x)=\displaystyle \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\)
ここで,\(f(x+h)=(x+h)^3\),\(f(x)=x^3\)を代入すると,
\(f’(x)=\displaystyle \lim_{h \to 0}\frac{(x+h)^3-x^3}{h}\)
\(f’(x)=\displaystyle \lim_{h \to 0}\frac{3x^2h+3xh^2+h^3}{h}\)
\(f’(x)=\displaystyle \lim_{h \to 0}3x^2+\underbrace{3xh}_{0}+\underbrace{h^2}_0\)
\(h\)は0とほぼ同じなので,\(h\)がかかっている項は0になります。よって,
\(f’(x)=3x^2\)
<終>
例題7:\(x^n\)の導関数を微分の定義に従って求めましょう。これは,割と難しいです。
例題7解答:
\(f’(x)=\displaystyle \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\)
ここで,\(f(x+h)=(x+h)^n\),\(f(x)=x^n\)を代入すると,
\(f’(x)=\displaystyle \lim_{h \to 0}\frac{(x+h)^n-x^n}{h}\)
\(f’(x)=\displaystyle \lim_{h \to 0}\frac{\cancel{h}((x+h)^{n-1}+(x+h)^{n-2}x+\cdots+x^n)}{\cancel{h}}\)
\(f’(x)=x^{n-1}+x^{n-1}+\cdots+x^{n-1}\)
\(x^{n-1}\)の項は\(n\)項あるので,
\(f’(x)=nx^{n-1}\)
<終>
https://cupuasu.club/dream-psychology/
微分のやり方:まとめ
$$(x^n)’=nx^{n-1}$$
$$(c)’=0$$
関数\(f(x)\)の導関数\(f’(x)\)は,
$$f’(x)=\displaystyle \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} $$
関連記事
微分積分学ー>

数列ー>




最後に
微分の定義は,微分の公式を証明するために使われていて,普段はあまり使われません。これから,微分についての記事を書いていきますが,証明も交えながらやります。\(\cancel{公式の証明の執筆が1番楽}\)