$$\require{\cancel}$$
この記事を読むメリット
☑ガウスの法則を使って，電界を素早く求めることが出来るようになる。
☑電界から電位への計算を積分で求められるようになる
☑いかにガウスの法則が便利なのかがわかる。
前回の記事を読んでいない方はまずこちらから－＞
ガウスの法則は対称性のある電界にのみ有効
閉曲面\(S\)(以降ガウス面と呼ぶ)をとったとき，ガウスの法則は，次式で定義されています。
$$\int_{S}E･dS=\frac{1}{\varepsilon_0}\sum Q$$
ガウスの法則に関する記事->
- ガウスの法則は，対称性のある電界を求めることに使われますが，その逆，対称性のない電界を求めることは出来ません。今回は，ガウスの法則を適用して，電界や電位を求める問題を解いていきます。
ガウスの法則：無限長線電荷の電界
問題1：
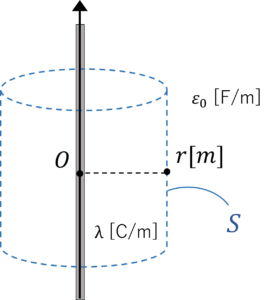
\(z\)軸上に線電荷密度\(λ\)[C/m]の無限長線電荷群を配置するとき，点P\(x,y,0\)における電界\(E\)を求めましょう。ただし，真空中の誘電率は\(\varepsilon_0\)[F/m](ファラド毎メートル)とします。
図1．無限長線電荷群
解答例－＞
半径\(r\)，高さ\(h\)の円柱状ガウス面\(S\)をとります。
すると，
ガウス面から出る，電気力線の本数は，\(\frac{1}{\varepsilon_0}\sum Q\)本なので，
\(\int_S E･dS=\frac{1}{\varepsilon_0}\times\underbrace{\sum Q}_{ガウス面内の電荷の総量}\)
まず，右辺を変形すると，
\(\frac{1}{\varepsilon_0}\sum Q=\frac{1}{\varepsilon_0}λh\)
です。
次に，左辺の\(S\)を3分割します。
円柱側面を\(S_2\)，円柱底面を\(S_1\)，\(S_3\)とおくと，
\(\int_{S_1}\underbrace{|E|i_r･i_zdS_1}_{=0}+\int_{S_2}|E|i_r･i_rdS_2 +\int_{S_3}\underbrace{|E|i_r･(-i_z)dS_3}_{=0}=\frac{λh}{\varepsilon_0}\)
面\(S_1\)と面\(S_3\)からは，電気力線が出ていかない！
\(\int_{S_2}E･dS_2=\frac{λh}{\varepsilon_0}\)
電界\(E\)は，\(S_2\)を均等に通過する(対称性を持つ)ので，
\(|E|\underbrace{\int_{S_2}dS_2}_{S_2の面積}=\frac{λh}{\varepsilon_0}\)
\(|E|2\pi r\cancel{h}=\frac{λ\cancel{h}}{\varepsilon_0}\)
\(|E|=\frac{λ}{2\pi r\varepsilon_0}\)
よって，円筒座標系の単位ベクトル\(i_r\)を用いて表すと，点\((x,y,0)\)における電界\(E\)は，
\(E=\frac{λ}{2\pi r\varepsilon_0}i_r\)[V/m]
<終>
因みに直交座標系で表すと。
\(E=\frac{λ}{2\pi r\varepsilon_0 (x^2+y^2)}(-y,x,0)\)[V/m]
となります。
おそらく理解できないと思いますが，次へ進んでから，後で理解しましょう。
ガウスの法則：無限平面電荷群
問題2：
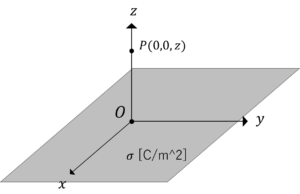
直交座標系\(xyz\)において，\(x-y\)平面に面電荷密度\(σ\)[C/m^2]が均等に分布しているとき，点\(0,0,z\)における電界\(E\)を求めましょう。ただし，真空の誘電率は\(\varepsilon_0\)[F/m]とします。図2．無限平面電荷群
解答例－＞
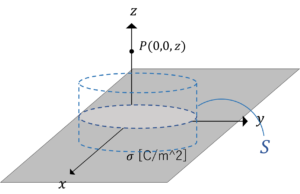
\(x-y\)平面を貫く円柱状ガウス面\(S\)を考えます。
ガウスの法則より，
\(\int_{S}E･dS=\frac{1}{\varepsilon_0}\times\underbrace{\sum Q}_{ガウス面内の電荷の総量}\)
まず，右辺は，円柱状ガウス面の底面積を\(S’\)とすると，
\(\frac{1}{\varepsilon_0}\sum Q=\frac{1}{\varepsilon_0}\sigma S’\)
続いて，左辺を先ほど同様，面を3つに分解します。
側面を\(S_2\)，上面下面を\(S_1，S_3\)とおきます。
\(\int_{S_1}E･dS_1+\int_{S_2}\underbrace{E･dS_2}_{=0}+\int_{S_3}E･dS_3=\frac{\sigma S’}{\varepsilon_0}\)
側面\(S_2\)から電気力線は出て行かない！
\(\int_{S_1}|E|i_z･i_zdS_1+\int_{S_3}-|E|i_z･(-i_z)dS_3=\frac{\sigma S’}{\varepsilon_0}\)
電気力線は，\(S_1\)と\(S_3\)を均等に通過するので，
\(|E|\underbrace{\int_{S_1}dS_1}_{S_1の面積}+|E|\underbrace{\int_{S_3}dS_3}_{S_3の面積}=\frac{\sigma S’}{\varepsilon_0}\)
\(|E|\underbrace{S’}_{S_1の面積}+|E|\underbrace{S’}_{S_3の面積}=\frac{\sigma S’}{\varepsilon_0}\)
\(2|E|\cancel{S’}=\frac{\sigma \cancel{S’}}{\varepsilon_0}\)
\(|E|=\frac{\sigma}{2\varepsilon_0}\)
よって，電界\(E\)は，\(z\)軸方向の単位ベクトル\(i_z\)を用いて表すと，
\(E=\frac{\sigma}{2\varepsilon_0}i_z\)[V/m]\(z> 0\)
\(E=-\frac{\sigma}{2\varepsilon_0}i_z\)[V/m]\(z<0\)
<終>
ガウスの法則：無限円柱電荷群(ケーブル)
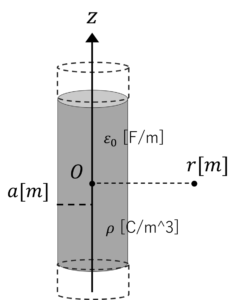
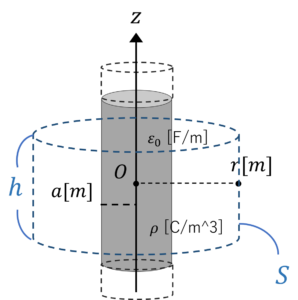
問題3：\(z\)軸上に無限に続く円柱導体を配置した。導体に帯電する電荷密度\(\rho\)[C/m^3]，真空の誘電率は\(\varepsilon_0\)のとき，円柱導体から垂直に\(r\)だけ離れた点における電界\(E\)を求めましょう。
(1) \(r\leq a\)のときの電界\(E\)
(2) \(r\geq a\)のときの電界\(E\)図3．無限に続く円柱導体
解答例－＞
導体を囲む円柱状のガウス面\(S\)をとると，
ガウスの法則より，
\(\int_{S}E･dS=\frac{1}{\varepsilon_0}\sum Q\)
右辺について，ガウス面が包む空間の体積を\(V\)とすると，
\(\frac{1}{\varepsilon_0}\sum Q=\frac{1}{\varepsilon_0}\int_{V}\rho dV\)
\(\frac{1}{\varepsilon_0}\sum Q=\frac{\rho}{\varepsilon_0}\times\underbrace{\int_{V}dV}_{半径aで高さhの円柱の体積}\)
\(=\frac{\rho}{\varepsilon_0}\pi r^2h\)
次に，左辺について，面\(S\)を3つに分解します。
上下面を\(S_1\)，側面を\(S_2\)とおくと，
\(\int_{S_1}\underbrace{|E|i_r･i_zdS_1}_{=0}+\int_{S_2}|E|i_r･i_rdS_2+\int_{S_3}\underbrace{|E|i_r･(-i_z)dS_3}_{=0}=\frac{\rho}{\varepsilon_0}\pi r^2h\)
面\(S_1\)と面\(S_3\)からは電気力線は出ていかない！
\(\int_{S_2}E･dS_2=\frac{\rho}{\varepsilon_0}\pi r^2h\)
電気力線は，面\(S_2\)に対して均等に流出するので，
\(|E|\underbrace{\int_{S_2}dS_2}_{面S_2の面積}=\frac{\rho}{\varepsilon_0}\pi r^2h\)
\(|E|2\cancel{\pi} r\cancel{h}=\frac{\rho}{\varepsilon_0}\cancel{\pi}r^2\cancel{h}\)
\(|E|2r=\frac{\rho}{\varepsilon_0}r^2\)
(1) \(r\leq a\)のとき，
\(|E|=\frac{\rho r}{2\varepsilon_0}\)[V/m]
\(E=\frac{\rho r}{2\varepsilon_0 r}i_r\)[V/m]
\(i_r\)は，円筒座標の\(r\)方向の単位ベクトル
(2) \(r\geq a\)のとき，
\(E=\frac{\rho a^2}{2\varepsilon_0 r}i_r\)
\(i_r\)は，円筒座標の\(r\)方向の単位ベクトル
<終>
ガウスの法則：導体球が作る電界
問題4：
半径\(a\)，電荷密度\(\rho\)[C/m^3]の球状電荷群がある。真空の誘電率が\(\varepsilon_0\)[F/m]のとき，球状電荷群から\(r\)離れた点における電界\(E\)と電位\(\phi\)を求めましょう。(1) \(r\leq a\)のとき，
(2) \(r\geq a\)のとき，
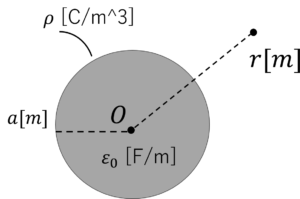
図4．球状電荷群
解答例－＞
半径\(r\)の球状ガウス面を取ります。
ガウスの法則より，
\(\int_{S}E･dS=\frac{1}{\varepsilon_0}\sum Q\)
まず，右辺について，
\(\frac{1}{\varepsilon_0}\sum Q=\frac{1}{\varepsilon_0}\int_{V}\rho dV\)
\(=\frac{\rho}{\varepsilon_0} \underbrace{\int_{V}dV}_{半径rの球の体積}=\frac{\rho}{\varepsilon_0}\frac{4}{3}\pi r^3\)
次に，左辺を変形すると，
\(=\int_{S}|E|i_r･i_r dS=\frac{\rho}{3\varepsilon_0}4\pi r^3\)
ここで，電気力線は，面\(S\)から均等に流出するので，
\(=|E|\underbrace{\int_{S}dS}_{面Sの面積}=\frac{\rho}{3\varepsilon_0}4\pi r^3\)
\(=|E|\cancel{4\pi} r^2=\frac{\rho}{3\varepsilon_0}\cancel{4\pi} r^3\)
(1) \(r\leq a\)のとき，
\(|E|=\frac{\rho r}{3\varepsilon_0}\)
\(E=\frac{\rho r}{3\varepsilon_0}i_r\)
\(i_r\)は，極座標の\(r\)方向の単位ベクトル
(2) \(r\geq a\)のとき，
\(|E|=\frac{\rho a^3}{3\varepsilon_0 r^2}i_r\)
\(E=\frac{\rho a^3}{3\varepsilon_0 r^2}i_r\)
\(i_r\)は，極座標の\(r\)方向の単位ベクトル
－＞更に，電界から電位\(phi\)を求めます。
(1) \(r\leq a\)のとき，[電磁気学]電界と電位電磁気学初心者の勉強を足止めする記事となっております。電界と電位についてのざっくりとした説明と，例題を載せています。実は，電位は電界のベクトル戦績分で，電界は，電位の勾配で表されます。...\(\phi=-\int_{\infty}^{r}\frac{\rho a^3}{3\varepsilon_0 r^2}i_r･i_rdr\)
\(\phi=[\frac{\rho a^3}{3\varepsilon_0 r}]_{\infty}^{r}=\frac{\rho a^3}{3 \varepsilon_0 r}\)
(2) \(r\geq a\)のとき，
\(\phi=-\int_{\infty}^{a}\frac{\rho a^3}{3\varepsilon_0 r^2}i_r･i_rdr-\int_{a}^{r}\frac{\rho r}{3\varepsilon_0}i_r･i_rdr\)
\(\phi=[\frac{\rho a^3}{3\varepsilon_0 r}]_{\infty}^{r}-[\frac{\rho r^2}{6\varepsilon_0}]_{a}^{r}\)
\(=\frac{\rho a^2}{3 \varepsilon_0}+\frac{\rho a^2}{6 \varepsilon_0}-\frac{\rho r^2}{6\varepsilon_0}\)
\(=\frac{\rho a^2}{2\varepsilon_0}-\frac{\rho r^2}{6\varepsilon_0}\)
<終>
ガウスの法則：関連問題
発展問題
1．平行平板コンデンサの電界と電位
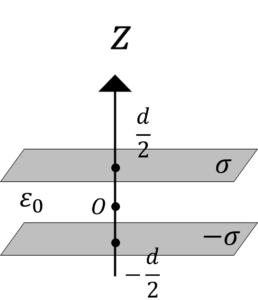
2．同軸ケーブルの電界と電位
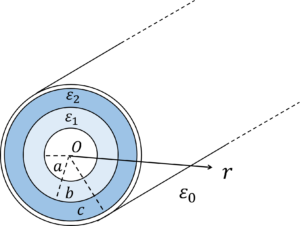
3．同心球の電界と電位
電験2種
電験3種
前回の電磁気学の記事
[電磁気学]電界と電位電磁気学初心者の勉強を足止めする記事となっております。電界と電位についてのざっくりとした説明と，例題を載せています。実は，電位は電界のベクトル戦績分で，電界は，電位の勾配で表されます。...次の電磁気学の記事
[ポワソン方程式]電界電位の相互関係式電界は電位の勾配で表されます。電界，電位，ガウスの法則をうまく組み合わせたのがポワソン方程式です。途中式を丁寧に書いています。電位から電界を求める例題。ポワソン方程式に関する例題を紹介します。電磁気学の計算に慣れていない人向けの記事になります。...ガウスの法則まとめ
電界まとめ点電荷が作る電界，電位
$$E=\frac{Q}{4\pi \varepsilon_0 r^2}i_r$$
$$\phi=\frac{Q}{4\pi\varepsilon_0 r}$$無限長線電荷群が作る電界
$$E=\frac{λ}{2\pi \varepsilon_0 r}i_r$$無限平面電荷群が作る電界
$$E=\frac{\sigma}{2\varepsilon_0}i_z (z>0)$$
$$E=-\frac{\sigma}{2\varepsilon_0}i_z (z<0)$$無限円柱電荷群が作る電界
$$E=\frac{\rho r}{3\varepsilon_0}i_r (r\leq a)$$
$$ E=\frac{\rho a^2}{3\varepsilon_0 r}i_r (r\geq a)$$球状電荷群が作る電界･電位
$$E=\frac{\rho a^3}{3\varepsilon_0 r^2}i_r$$
$$E=\frac{\rho r}{3\varepsilon_0}i_r$$最後に
大学の電磁気学のテストでは，私の解答例のように順を追って丁寧に解かないと良い点を取ることが出来ません。とはいえ，私の解答例も完璧ではありません。この解答例を参考にするのは一向にかまいませんが，出来れば，自分に合わせた解き方にカスタマイズして欲しいです。
