$$\require{\cancel}$$
この記事を読むメリット
☑電磁気学に出てくる電界に関する公式をすんなり覚えるための知識を身につけることができる
☑電界に関するガウスの法則を図と例題を通して理解できる
前回の記事を読んでいない方は,電界(電場)\(E\)を求める公式だけでも,確認しておいてください。

ガウスの法則:電気力線
電気力線は,下図のように電界\(E\)を表す矢印のことです。
電気力線の性質:
1. 正電荷から出て負電荷に入る
2. 電気力線は,互いに交差しない
1番目の性質は,図1.のような状況を考えると間違っているように見えます。
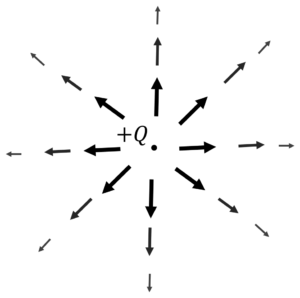
図1.\(Q\)の電気力線
図1.のような状態だと,負の電荷がないから,電気力線は伸びていかないのでは?と思う人がいるかもしれません。
実は,図1.には負の電荷はあります!
電磁気学的考え方によると,図2のように,無限遠点に\(-Q\)の電荷をばらまかれていると仮定することで,正電荷の電気力線が同心円状に伸びていくことに納得がいきます。
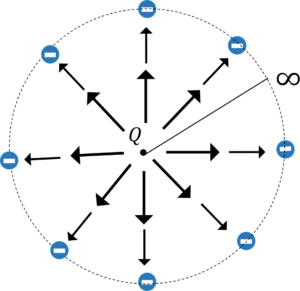
図2.\(Q\)を無限遠点で取り囲む負の電荷群
電気力線の数え方
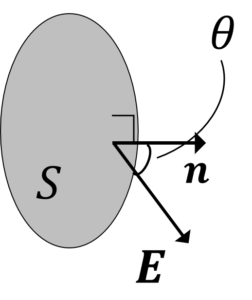
電気力線の本数を\(N\)は,
$$N=E・nS=E\cos \theta S\tag{1}$$
という風に数えます。
\(n\)は面\(S\)に垂直な単位ベクトルです。
\(E・n\)は,\(E\)と\(n\)との内積をとっているので,
\(E・n=|E|cos\theta\)
と表せることがわかります。
ここで,\(E・n\)の意味についてもう少し深く考えましょう。
結論から言うと,\(E・n\)は,面を通る\(E\)を数え,面を通らない\(E\)を数えないことを意味します。
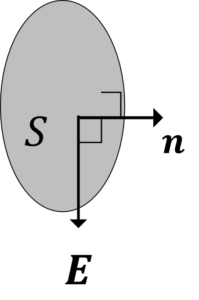
例えば,\(E\)と\(n\)のなす角が\(\frac{\pi}{2}\)の場合は下の図のようになり,
図3.面\(S\)と電界\(E\)が平行
電気力線は,面\(S\)を通過しません。式で書くと,
\(E・n=|E|cos \frac{\pi}{2}=0\)
では,\(E\)と\(n\)なす角が\(\pi\)のときは,どうでしょうか?
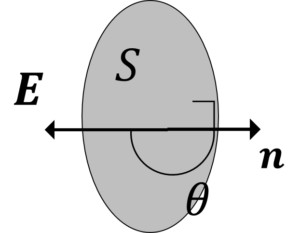
図4.面\(S\)と電界\(E\)が垂直
この場合は,面の内側からは電気力線は出ていきませんが,面の外側から電荷が入り込むので,
\(E・n=|E|\cos \pi=-|E|\)
となります。
このように,\(E・n\)は,面を通る電気力線\(E\)だけを数える性質があります。
教授様様のありがたいご指摘を逃れる為の\(S\)を通る電気力線の本数\(N\)
$$N=\oint_{S}E・ndS\tag{2}$$
式(2)のような積分は通常,ベクトル面積分と呼ばれます。
実は,式(1)では,電気力線の本数\(N\)を数えるには不完全でして,
下の図のように,面\(S\)の場所ごとに電気力線の本数が違う場合は式(1)では,電気力線の本数を正しく数えきれない人が続出します。だから,式(2)で,電気力線の本数を正しく定義してあげたというわけです。
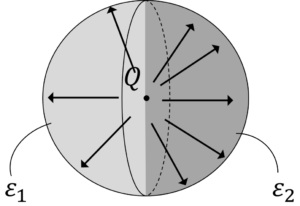
図5.左と右で電気力線の本数が違う例
ガウスの法則:例題1
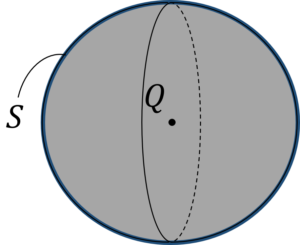
下の図のような状況を仮定します。この時,\(Q\)[C]の電荷を取り囲む半径\(r\)の球面から,\(\frac{Q}{\varepsilon}\)本の電気力線が出ていくことを示しましょう。ただし,電荷内部の誘電率は,\(\varepsilon\)とします。
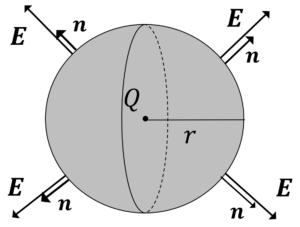
例題1解答:
式(1)から\(N\)は,
$$N=E\cos \theta S$$
です。ここで,面Sに垂直なベクトル\(n\)と電界ベクトル\(E\)は平行なので,\(N\)は,
$$N=ES$$
と書き換えられます。
ここで,電界\(E\)と面Sの表面積\(S\)について,以下の等式が成り立ちます。
\(E=\frac{Q}{4\pi \varepsilon r^2}\)
\(S=4\pi r^2\)
この2式を\(N\)の式に代入すると,\(N\)は,
\(N=ES=\frac{Q}{\cancel{4\pi}\varepsilon \cancel{r^2}}\cancel{4\pi r^2}=\frac{Q}{\varepsilon}\)
よって,電気力線の本数は\(\frac{Q}{\varepsilon}\)本になります。
<終>
電界(電場)のガウスの法則
点電荷が1つの場合のガウスの法則
ガウスの法則は,次式で表されます。
$$N=\oint_{S}E・ndS=\frac{Q}{\varepsilon}\tag{3}$$
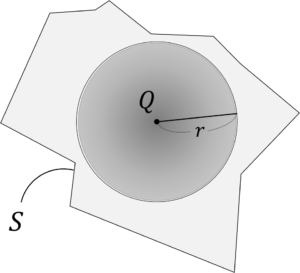
\(S\)は電荷を囲む任意の閉曲面(以降ガウス面と呼びます)
式(3)からガウスの法則は,2つのことを主張しています。
1.\(Q\)[C]の電荷から出る電気力線の本数は,\(\frac{Q}{\varepsilon}\)本
2.0[C]の電荷から出る電気力線の本数は,0本
2番目の主張は,1番目の主張から容易に導かれますが,
2番目の主張はとても大事です。
ガウスの法則:証明
1個の電荷を含む任意の閉曲面から外に出る電気力線の本数\(N\)が本当に\(\frac{Q}{\varepsilon}\)なのか確かめます。
例えば,例題1のように,\(Q\)[C]の電荷を覆う球状のガウス面を取ります。
このとき,ガウス面から出る電気力線の本数\(N_1\)は,\(\frac{Q}{\varepsilon}\)本です。
\(N_1=\frac{Q}{\varepsilon}\)
次に,下の図のようにガウス面を取りましょう。
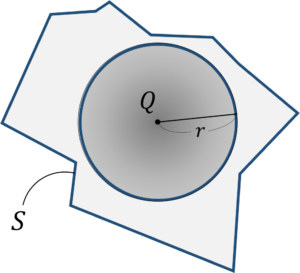
そうすると,ガウス面内には,0[C]の電荷があるので,電気力線は,吸い込まれたり吐き出されたりしません。
よって,ガウス面から出る電気力線の本数\(N_2\)は,\(0\)本です。
\(N_2=0\)
そうすると,\(N_1+N_2\)は,電荷を含む任意の閉曲面から外に出る電気力線の本数\(N\)と一致します。
\(N=N_1+N_2=\frac{Q}{\varepsilon}\)
<終>
\(N\)の電荷に関するガウスの法則
今度は,誘電率\(\varepsilon\)の領域内に\(M\)個の電荷を用意します。
下の図のように,\(M\)個の電荷のうち,\(N\)個の電荷をガウス面でくくります。

このとき,ガウス面から出て行く電気力線の本数\(N\)は,
$$N=\oint_{S}E・ndS=\sum_{i=1}^{N}\frac{Q_i}{\varepsilon}\tag{4}$$
となります。この式は,電荷が,電気力線を吐き出したり吸い込んだりする穴のようなものであるということを暗に示しています。
ガウスの法則:例題2
例題2解答:
電界に関するガウスの法則から
\(N=\frac{(10+2-12)\times 10^{^6}}{\varepsilon}=0\)本
ガウスの法則の関連問題
電験2種
電験3種
円筒導体の静電容量
前回の記事

次回の記事

次回の記事にベクトル線積分が登場しますので,補足事項として->

ガウスの法則のまとめ
電界を求める式
$$|E|=\frac{Q}{4\pi \epsilon |r-r’|^3}(r-r’)$$
電界に関するガウスの法則
$$\oint_{S}E・ndS=\frac{1}{\varepsilon}\sum_{i=1}^{N}Q_{i}$$
点電荷は,電気力線を吐き出したり吸い込んだりする穴のようなもの
最後に
先日Twitterにて,私が勉強の際に利用しているサイトの運営者,電気の神髄の「摺り足の加藤」さんと,電験王の「たけちゃん」さんのお二方に初めて返信をいただいたこともあって,テンション爆上がりしていました。これからも引き続き頑張ろうと思った1日でした。