この記事を読むメリット
☑電位の定義を電磁気学的に理解できます。
☑あわよくば，ベクトル線積分が出来るようになります。
電位差と電位の定義
仕事の定義を思いだそう
電位について考える前に，電界中で，\(B\)から\(A\)まで電荷を運ぶときの仕事について考えます。
$$仕事＝受ける力×距離×\cos \theta [Nm]$$
でした。
加える力を\(F’\)，受ける力(重力など)を\(F\)と置き，進む方向を表すベクトルを\(dr\)とすると，
$$W_{BA}=\int_{A}^{B}F’・dr$$
図1．重力による位置エネルギー
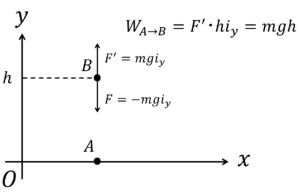
補足：\(F’・dr\)は，\(F’\cos \theta d|r|\)と表すことも出来ますが，\(\theta\)を定義するのが面倒なので，\(F’・dr\)のように内積で表すことが普通です。
図より，\(F’=-F\)なので，\(W_{BA}\)は，
$$W_{BA}=-\int_{A}^{B}F・dr\tag{1}$$
\(F\)：受ける力(重力など)
\(dr\)：運ぶ向きを表す微小な位置ベクトル
電位と電位差の定義とその違い
ようやく本題に入ります。
電位差\(\phi_{BA}\)は，次式で表されます。
$$\phi_{BA}=-\int_{A}^{B}E・dr\tag{2}$$
図2．\(\phi_B\)から見た\(\phi_A\)
む，この式はどこかで見覚えがありますね！
式(2)の両辺に電荷\(Q\)をかけると，
$$Q\phi_{BA}=-\int_{A}^{B}QE・dr$$
\(W_{BA}=Q\phi_{BA}\)，\(F=QE\)から，
$$W_{BA}=-\int_{A}^{B}F・dr$$
となって式(1)と一致します。
電位\(phi\)の定義は，
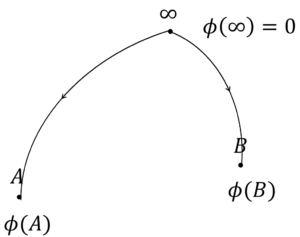
$$\phi=-\int_{\infty}^{B}E・dr\tag{3}$$
電位は，電界が0になる点を基準に選びます。電界が0になる点は，電界の式から，\(r=\infty\)のときであることは明らかです。
$$E(\infty)=\frac{Q}{4\pi \varepsilon (\infty)^2}=0$$
図3．電荷があっても，無限遠点の電位は0
また，電位差\(V_{BA}\)は，電位\(V_B\)と電位\(V_A\)の差であることもわかります。
$$\phi_{BA}=\phi_B-\phi_A$$
図4．無限遠点を基準とした2つの電位\(\phi_A\)，\(\phi_B\)
電位に関する例題
例題1：
誘電率\(\varepsilon\)の座標空間上に\(Q\)[C]の電荷を点\((a,0)\)に置いたとき，
(1) \((0,y)\)に働く電界\(E_1\)と電位\(\phi_1\)を求めましょう。ただし，電位の基準は，無限遠点とします。
(2) \(-Q\)[C]の電荷を\((-a,0)\)に置いたとき，\((0,y)\)に働く電界\(E_2\)と電位\(\phi_2\)を求めましょう。
ベクトル線積分を忘れた方－＞
例題1解答
(1)解答例
電界\(E\)について，
\(E=\frac{Q}{4\pi\varepsilon |(0,y)- (a,0)|^{3}}((0,y)- (a,0))\)
\(E=\frac{Q}{4\pi\varepsilon |(- a,y)|^{3}}(- a,y)\)
\(E=\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^{3}}(- a,y)\)[V/m]
<終>
電位\(\phi\)について，
\(\phi=-\int_{\infty}^{(0,y)} E･dr\)
\(y\)軸方向の単位ベクトル(大きさ1のベクトル)を\((0,1)\)とすると，\(dr\)は，
\((0,1)dy\)したがって，電位\(\phi\)は，
\(\phi=-\int_{\infty}^{y}\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^{3}}(-a,y)･(0,1)dy\)
\(\phi=-\int_{\infty}^{y}\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^{3}}ydy\)
\(\phi=[\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}}]_{\infty}^{y}\)
\(\phi=\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}}\)[V]
単位ベクトルは，今回は簡単のため\((0,1)\)としましたが，無限遠点に向かう単位ベクトルであれば，\((1,0)\)や，\((-a,y)\)など，任意にとってかまいません。
<終>
(2)解答
(1) の結果を利用して，\((-a,0)\)にある\(-Q\)[C]の電荷が点\((0,y)\)に作る電界を計算します。
\(\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}}(-a,-y)\)
これらを踏まえると，電界\(E_2\)は重ね合わせの原理より，
\(E_2=\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^3}(-a,-y)+\frac{Q}{4\pi \varepsilon \sqrt{a^2+y^2}^3}(-a,y)\)[V/m]
\(E_2=\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^3}(-2a,0)\)
電位\(\phi_2\)について，
\(\phi_2=\int_{\infty}^{(0,y)}E･dr\)
\(y\)軸方向の単位ベクトル(大きさ1のベクトル)を\((0,1)\)とすると，\(dr\)は，\((0,1)dy\)
したがって，電位\(phi\)は，
\(\phi=-\int_{\infty}^{y}\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^3}(-2a,0)･(0,1)dy\)
\(\phi=-\int_{\infty}^{y}\frac{Q}{4\pi\varepsilon \sqrt{a^2+y^2}^3}･0dy=0\)
よって，
\(\phi=0\)V
<終>
電界と電位：関連問題
電験1種
電験2種
電験3種
前回の電磁気学の記事
次の電磁気学の記事
電界と電位：まとめ
与える力を\(F\)とすると，仕事\(W_{BA}\)は，
$$W_{BA}=\int_{A}^{B}F･dr$$
受ける力を\(F\)とすると，仕事\(\phi_{BA}\)は，
$$\phi_{BA}=-\int_{A}^{B}E･dr$$
$$W=QV$$
$$F=QE$$
最後に
今回は，電界から電位を求めましたが，逆に電位から電界を計算する方法も存在します。その方法は，ベクトルの微分とスカラー場の勾配の計算方法などを熟知していれば，マスター出来ます。計算方法がわからない人は，ベクトル解析という参考書を使って，計算練習してみるのが良いと思います。
