[電磁気学]電界(電場)と電界の重ね合わせ[例題付き]

$$\require{\cancel}$$

ユキ

「電界」は電気屋さんの言葉，「電場」は物理屋さんの言葉，どうも，ユキです。

今回は，電場(電界)についてのお話です。

電界$E$の定義

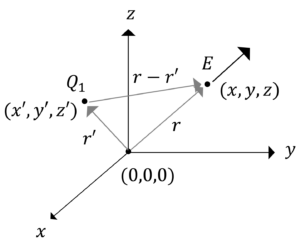
原点に電荷$Q_1$を置いたときの点$(x,y,z)$における電界$E$は次式で表されます。

$$E=\frac{Q_1}{4\pi \varepsilon |r|^3}r=\frac{Q_1}{4\pi \varepsilon \sqrt{x^2+y^2+z^2}^{3}}(x,y,z)\tag{1}$$

電荷：$Q_1$[C]
位置：$r$[m]
誘電率：$\varepsilon$[F/m]
電界：$E$[V/m]

図1．原点に電荷$Q_1$を置いたときの電界$E$

電界の性質

電界の性質

1．プラスの電荷は外向きに電界を作る

2．マイナスの電荷は内向きに電界を作る

3．電界の大きさは電荷の距離の逆二乗に比例する

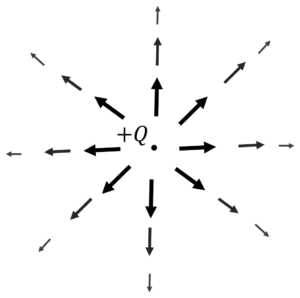
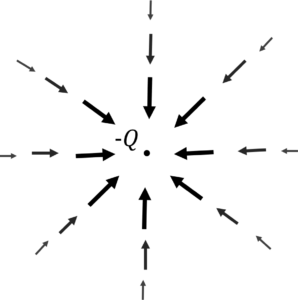
図2．$+Q$における電界の分布(左図)，$-Q$における電界の分布(右図)

例題1

例題1：原点に電荷$Q_1$をおいたとき，点$(x,0,0)$における電界$E$を求めましょう。ただし，誘電率は$\varepsilon$とします。

例題1解答：

電界の定義式より

$E=\frac{Q_1}{4\pi \varepsilon|r|^3}r$

ここで，題意から$r=(x,0,0)$，$|r|=x^2$なので，

$E=\frac{Q_1}{4\pi \varepsilon \sqrt{x^2}^3}(x,0,0)=\frac{Q_1}{4\pi \varepsilon x^2}(1,0,0)$

電界の定義式の拡張

式(1)だと，
電荷を原点にしかおけなくなってしまい使いづらいので，公式を拡張しましょう。

点$(x’,y’,z’)$に電荷$Q_1$を置いたときの点$(x,y,z)$における電界$E$は次式で表されます。

$$E=\frac{Q_1}{4\pi \varepsilon |r-r’|^3}(r-r’)$$

$=\frac{Q_1}{4\pi \varepsilon \sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}^{3}}(x-x’,y-y’,z-z’)\tag{2}$

電荷：$Q_1$[C]
位置：$r$[m]
誘電率：$\varepsilon$[F/m]
電界：$E$[V/m]

図3．点$(x’,y’,z’)$に電荷$Q_1$を置いたときの電界$E$

式(2)は一見文字が多くて複雑そうに見えますが，実は，式(1)と同じことを主張しています。

$r$ベクトルを$r’$だけ平行移動させると，下の図4のようになります。

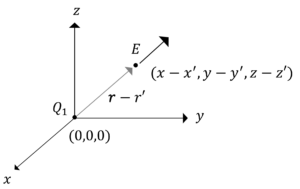
図4．点$(0,0,0)$に電荷$Q_1$を置いたときの電界$E$

また，式(2)の$(x’,y’,z’)=(0,0,0)$とすれば，式(1)と一致しているので，式(2)は式(1)の拡張版と言うことも出来ます。

例題2

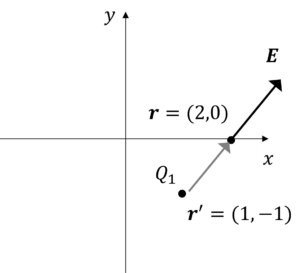
例題2：以下の図のように，点$1,-1$に電荷$Q_1$をおいたとき，点$(2,0)$における電界$E$を求めましょう。ただし，誘電率は$\varepsilon$とします。

例題2解答：

式(2)から，電界$E$は

$ E=\frac{Q_1}{4\pi \varepsilon |r-r’|^3}(r-r’)$

ここで，$r-r’=(1,1)$，$|r-r’|=\sqrt{1^2+1^2}=\sqrt{2}$より，

$E=\frac{Q_1}{4\pi \varepsilon \sqrt{2}^3}(1,1,0)=\frac{Q_1}{8\pi\varepsilon}(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0)$

となります。

<終>

電界の重ね合わせ

電界は重ね合わせが成立することが知られています。

$$E=E_1+E_2$$

$Q_1$と$Q_2$が作る電界：$E$[V/m]
$Q_1$が作る電界$E_1$[V/m]
$Q_2$が作る電界$E_2$[V/m]

図4．電界$E_1$と電界$E_2$の重ね合わせ

例題3

例題3：以下の図のように，$Q$[C]の電荷を$(-1,0)$，$-4Q$の電荷を$4,0$に配置した。誘電率を$\varepsilon$とするとき，以下の問に答えよ。
図(1) $x$軸上で，電界の強さが0になる点を求めよ。
(2) 点$(0,2)$の電界$E$[V/m]を求めよ。

例題3解答：

(1)解答：

電界が0になる点を$(x,0)$と置くと，

$(x,0)$における電界$E$は次のように表されます。

$E=\frac{Q}{4\pi \varepsilon \sqrt{(x+1)^2}^3}(x+1,0)+ \frac{-4Q}{4\pi \varepsilon \sqrt{(x-4)^2}^3}(x-4,0)$

ただし，$x$が存在しうる範囲は，$x<-6，4<x$

$=\frac{Q}{4\pi\varepsilon}(\frac{1}{(x+1)^2}(1,0)+\frac{-4}{(x-4)^2})(x-4,0)=0$

$y$方向の電界は0なので，$x$方向のみを考えると，

$\frac{1}{(x+1)^2}-\frac{4}{(x-4)^2}=0$

$(x-4)^2=4(x+1)^2$

$(x-4)=\pm 2(x+1)$

$x \mp 2x=4\pm 2$