どうも,ユキです。今日は高校物理で最初に習う電気と磁気の公式と定理について言及していこうと思います。
クーロンの法則
クーロンの法則
$$F=\frac{Q_1Q_2}{4\pi\varepsilon r^2}\tag{1}$$
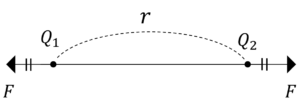
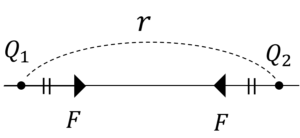
図1.\(Q_1\)と\(Q_2\)が同符号のとき 図2.\(Q_1\)と\(Q_2\)が異符号のとき
\(F\)[N] クーロン力の大きさ
\(\varepsilon\)[F/m] 誘電率
\(Q_1,Q_2\) 点電荷の電気量[C]
\(r\) 点電荷間の距離
クーロンの法則の定義式の右辺の数\(Q_1,Q_2\),\(\varepsilon\),は\(r\)がいくら動いても変化しないので,クーロン力\(F\)は,\(r\)だけに依存する関数とみなせますので,
$$F(r)= \frac{Q_1Q_2}{4\pi\varepsilon r^2}$$
このように書き表すこともできます。
電気量保存の法則
電気量保存の法則:物体同士のやりとりの前後で,電気量の総和は変わらない
この法則は,電気量が無からいきなり生成されたり,消滅したりしないことを保証する法則です。名前自体を覚える必要はありませんが,電気量の総和が変わらないという事実は,当たり前のように知っておいてください。
静電誘導
物質は,その電気の通しやすさの度合いよって以下の3つに分類されます。
導体,不導体(絶縁体),半導体
導体:金属のように電気をよく通す物質
不導体:塩化ナトリウム(NaCl),ゴム,紙などの電気を通しにくい物質
半導体:導体と不導体の中間。ケイ素(Si),ゲルマニウム(Ge)など
不導体,半導体,導体の電子の動きを見てみましょう。
1.不導体
図3.不導体の様子
不導体は,1つの正の電荷に対し,1つの負の電荷がくっついているので,不導体の負の電荷はおとなしいです。例えるなら,学校の教室でクラス全員が自分の座席に座っている状態です。
2.半導体
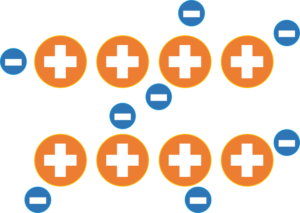

図4-1.半導体の様子
半導体は,先ほど同様,1つの正の電荷に対し,1つの負の電荷がくっついていますが,半導体の負の電荷は,不導体のそれに比べて少しざわついています。
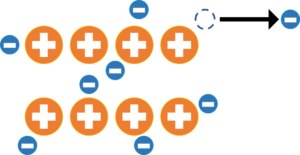
図4-2.熱が加わった半導体の様子
もし,この電荷に熱(エネルギー)でも加えようものなら,負の電荷の一部は座席から飛び出します。座席から飛び出した電子は,自由電子と呼ばれます。
3.導体
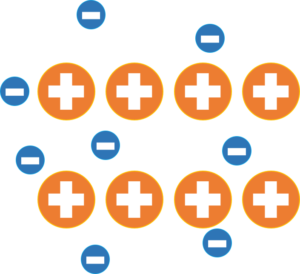
図5.導体の様子
全ての電子が自分の座席から飛び出している状態です。座席から飛び出している電子は,自由電子と呼ばれます。
導体,不導体に負に帯電した金属を近づける
1.導体に帯電体を近づける
1-1.負に帯電した導体棒を近づけた場合


図6.電気量0[C]の導体球
帯電していない(電気量0[C]の)導体球を用意します。ここで,負に帯電した導体棒を近づけると,導体棒から遠い側に負の電荷が集まるので,

図7-1.導体球に負に帯電した導体棒を近づける
このようになります。ただし,このままでは,電気量保存の法則\(^*\)に反してしまうので,

図7-2.導体球に負に帯電した導体棒を近づける
導体棒側に正の電荷を導体棒に近い位置に,反対側の負の電荷と同じ数だけ書き,帳尻を合わせます。
導体内の負の電荷は座席から飛び出せますので,導体内のすべての負の電荷は,帯電体から遠いところに逃げることができます。この現象を静電誘導といいます。
1-2.正に帯電した導体棒を近づけた場合
先ほど同様,帯電していない(電気量0[C]の)導体球を用意します。ここで,正に帯電した導体棒を近づけると,導体棒から遠い側に正の電荷が集まるので,


図7-1.導体球に負に帯電した導体棒を近づける
このようになります。ただし,このままでは,電気量保存の法則\(^*\)に反してしまうので,

図7-2.導体球に負に帯電した導体棒を近づける
導体棒側に負の電荷を導体棒に近い位置に,反対側の正の電荷と同じ数だけ書き,帳尻を合わせます。
2.不導体に帯電体を近づける
まず,先ほどの不導体を持ってきましょう。

図8-1.帯電体を近づける前の不導体
次に,負に帯電した導体棒を上から近づけると,

図8-2.帯電体を近づけたときの不導体
導体とは異なり,不導体の負の電荷は固定された自分の座席に着席したまま,帯電体から逃げますので,このようになります。このような静電誘導の現象を特に,誘電分極といいます
クーロン力に関する例題
例題1:
下の図のように,2点の電荷の間に電荷\(Q_0\)を置いたとき,\(Q_0\)に働く力がゼロになった。その位置\(x\)を求めよ。
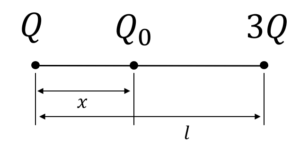
例題答え:
\(Q_0\)を置いたところは,左右の力がつりあっているので,以下の等式が成立します。
\(\underbrace{\frac{QQ_0}{4\pi\varepsilon x^2}}_{右向きの力}=\underbrace{\frac{3QQ_0}{4\pi\varepsilon(l-x)^2}}_{左向きの力}\) \(∵ F=\frac{Q_1Q_2}{4\pi\varepsilon r^2}\)
そして,\(x\)について解きます。
\(\frac{1}{x^2}=\frac{(\sqrt{3})^2}{(l-x)^2}\)
\((l-x)^2=(\sqrt{3}x)^2\)
\((l-x)=\sqrt{3}x\)
\((\sqrt{3}+1)x=l\)
\(x=\frac{l}{(\sqrt{3}+1)}\)
\(x=\frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)}\)
よって,
\(x=\frac{\sqrt{3}-1}{2}\)
関連問題
電験3種
次の電磁気学の記事


おさらい
1.クーロンの法則
$$F=\frac{Q_1Q_2}{4\pi\varepsilon r^2}$$
2.導体の静電誘導

3.不導体の静電誘導

不導体の静電誘導のことを特に,静電分極という
最後に
大学の電磁気学を勉強するためには,高校数学までの知識では足りず,大学で,微分積分学やベクトル解析学を学ばないといけません。なぜなら,大学の電磁気学の多くの参考書は,読者がこれらの数学の知識を持つことを前提にして作られているからです。そこで,私は,「高校までの知識で電磁気学を理解できるような記事を書けば需要があるのではないか」と考え,執筆に至ったわけです。