$$\require{\cancel}$$
今日は,電位から電界を求める方法についてお話ししていこうと思います。
この記事を読むメリット
☑電位と電界の関係を学べる
☑電位から電界を計算できるようになる
☑微分の進化形である,勾配の計算が出来るようになる。
電位と電界の関係
以前の記事で,電界から電位を求める式について学習しました。
$$\phi=-\int_{\infty}^{B}E・dr\tag{1}$$
以下の記事は,式(1)を使って実際に電界から電位を計算している記事になります。


ここまでで,電界から電位を計算する方法はわかりましたが,その逆,電位から電界を計算する方法についてお話します。
電位と電界には,以下の関係があります。
$$E=-∇\phi \tag{2}$$
これだけです。あれ,∇って何?
∇は,ベクトル付きの微分です。
$$∇=\frac{\partial }{\partial x}i_x+\frac{\partial }{\partial y}i_y+\frac{\partial}{\partial z}i_z\tag{3}$$
式(3)は,∇の基本式なので,覚えておいてください。
つまり,式(2)に式(3)を代入すると,電界の式は
$$E=-\frac{\partial \phi}{\partial x}i_x-\frac{\partial \phi}{\partial y}i_y-\frac{\partial \phi}{\partial z}i_z \tag{4}$$
となります。式が長くて面倒くさいと思います。
しかーし,1個の球電荷や,無限平板のような対称性の良い電界ならば,電界と電位の関係式は以下のようになります。
$$E=-\frac{\partial \phi}{\partial r}i_r\tag{5}$$
式(4)よりも,式(5)の方がすっきりしていますね。
やはりここでも,対称性が計算を簡単にしてくれました。
では,与えられた電位を式(4)と式(5)を駆使して,電界を求めましょう。
電位▶電界:例題
例題1:
原点にある1個の点電荷による電位は,\(\frac{Q}{4\pi\varepsilon_0 |r|}\)[V]であたえられています。このとき,電界\(E\)を求めましょう。
ただし,\(|r|=\sqrt{x^2+y^2+z^2}\)とします。
例題1解答->
まずは,式(4)を使いましょう。
電界\(E\)は,
$$E=-\frac{\partial \frac{Q}{4\pi\varepsilon_0 |r|}}{\partial x}i_x-\frac{\partial \frac{Q}{4\pi\varepsilon_0 |r|}}{\partial y}i_y-\frac{\partial \frac{Q}{4\pi\varepsilon_0 |r|}}{\partial z}i_z $$
まずは,共通因数をくくって,微分に関係ない項を外にだします。
\(E=-\frac{Q}{4\pi\varepsilon_0}(\frac{\partial }{\partial x}\frac{1}{|r|}i_x+\frac{\partial }{\partial y}\frac{1}{|r|}i_y+\frac{\partial}{\partial z}\frac{1}{|r|}i_z) \)
ここで,\(|r|=\sqrt{x^2+y^2+z^2}\)を使うと,
\(E=-\frac{Q}{4\pi\varepsilon_0}(\frac{\partial }{\partial x}\frac{1}{\sqrt{x^2+y^2+z^2}}i_x+\frac{\partial }{\partial y}\frac{1}{\sqrt{x^2+y^2+z^2}}i_y+\frac{\partial}{\partial z}\frac{1}{\sqrt{x^2+y^2+z^2}}i_z) \)
\(E=-\frac{Q}{4\pi\varepsilon_0}(\frac{-1}{\cancel{2}}\frac{\cancel{2}x}{(x^2+y^2+z^2)^{\frac{3}{2}}}i_x+\frac{-1}{\cancel{2}}\frac{\cancel{2}y}{(x^2+y^2+z^2)^{\frac{3}{2}}}i_y+\frac{-1}{\cancel{2}}\frac{\cancel{2}z}{(x^2+y^2+z^2)^{\frac{3}{2}}}i_z) \)
よって,電界\(E\)は
\(E=\frac{Q}{4\pi\varepsilon_0}\frac{xi_x+yi_y+zi_z}{(x^2+y^2+z^2)^{\frac{3}{2}}}\)[V/m]
ここで,電界\(E\)を極座標表示に変形しましょう。
極座標のベクトル\(|r|i_r\)は,\(|r|i_r=xi_x+yi_y+zi_z\)と表すことができ,\(|r|=\sqrt{x^2+y^2+z^2}\)
電界\(E\)は
\(E=\frac{Q|r|i_r}{4\pi\varepsilon_0 |r|^3}\)
\(E=\frac{\partial}{\partial r}\frac{Q}{4\pi\varepsilon_0 |r|^2}i_r \)[V/m]
となります。
<終>
続いて,式(5)を使って,電界を求めてみましょう。
\(E=-\frac{\partial}{\partial r}\frac{Q}{4\pi\varepsilon_0 |r|}i_r\)
\(E=\frac{\partial}{\partial r}\frac{Q}{4\pi\varepsilon_0 |r|^2}i_r \)[V/m]
となります。
式(4)で求めた電界\(E\)と式(5)で求めた電界\(E\)は一致しました。
<終>
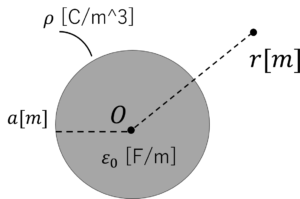
例題2:
半径\(a\)の球状電荷群の外側の電位\(\phi_{out}\)は,\(\phi_{out}=\frac{\rho a^3}{3\varepsilon_0 |r|}\)
内側の電位は,\(\phi_{in}=\frac{\rho a^2}{2\varepsilon_0 }-\frac{\rho |r|^2}{6\varepsilon_0}\)
このとき,球状電荷群の外側と内側の電界\(E_{out}\)と\(E_{in}\)を求めましょう。
ただし,\(|r|=\sqrt{x^2+y^2+z^2}\)とします。
例題2解答―>
\(E_{out}\)について,式(4)を適用します。
微分に関係ない項を外にくくり出すと,
\(E_{out}=-\frac{\rho a^3}{3\varepsilon_0}(\frac{\partial }{\partial x}\frac{1}{|r|}i_x+\frac{\partial }{\partial y}\frac{1}{|r|}i_y+\frac{\partial}{\partial z}\frac{1}{|r|}i_z)\)
\(|r|=\sqrt{x^2+y^2+z^2}\)より,
\(E_{out}=-\frac{\rho a^3}{3\varepsilon_0}(\frac{\partial }{\partial x}\frac{1}{\sqrt{x^2+y^2+z^2}}i_x+\frac{\partial }{\partial y}\frac{1}{\sqrt{x^2+y^2+z^2}}i_y+\frac{\partial}{\partial z}\frac{1}{\sqrt{x^2+y^2+z^2}}i_z)\)
\(E_{out}=-\frac{\rho a^3}{3\varepsilon_0} (\frac{-1}{\cancel{2}}\frac{\cancel{2}x}{(x^2+y^2+z^2)^{\frac{3}{2}}}i_x+\frac{-1}{\cancel{2}}\frac{\cancel{2}y}{(x^2+y^2+z^2)^{\frac{3}{2}}}i_y+\frac{-1}{\cancel{2}}\frac{\cancel{2}z}{(x^2+y^2+z^2)^{\frac{3}{2}}}i_z) \)
よって,電界\(E_{out}\)は,
\(E_{out}=\frac{\rho a^3}{3\varepsilon_0}\frac{xi_x+yi_y+zi_z}{(x^2+y^2+z^2)^{\frac{3}{2}}}\)[V/m]
ここで,電界\(E_{out}\)を極座標表示に変形すると,
\(|r|i_r=xi_x+yi_y+zi_z\),\(|r|=\sqrt{x^2+y^2+z^2}\)より
\(E_{out}=\frac{\rho a^3}{3\varepsilon_0 |r|^2}i_r\)
<終>
電界\(E_{out}\)について,式(5)を使うと,
\(E_{out}=-\frac{\partial}{\partial r}\frac{\rho a^3}{6\varepsilon_0 r}i_r\)
\(E_{out}=\frac{\rho a^3}{3\varepsilon_0 r^2}i_r\)
<終>
次に電界\(E_{in}\)を求めましょう。
式(4)を適用して,微分に関係ない項を外にくくり出すと
\(E_{in}=-\frac{\rho a^2}{2\varepsilon_0}(\frac{\partial }{\partial x}i_x+\frac{\partial }{\partial y}i_y+\frac{\partial}{\partial z}i_z)+\frac{\rho}{6\varepsilon_0}(\frac{\partial |r|^2}{\partial x}i_x+\frac{\partial |r|^2}{\partial y}i_y+\frac{\partial |r|^2}{\partial z}i_z)\)
\(|r|^2=x^2+y^2+z^2\)より,
\(E_{in}=0+\frac{\rho}{6\varepsilon_0}(\frac{\partial}{\partial x}(x^2+y^2+z^2)
i_x+\frac{\partial }{\partial y}(x^2+y^2+z^2)
i_y+\frac{\partial }{\partial z}(x^2+y^2+z^2)
i_z)\)
\(E_{in}=\frac{\rho}{3\varepsilon_0}(xi_x+yi_y+zi_z)\)
\(|r|i_r=xi_x+yi_y+zi_z\)とおくと,
\(E_{in}=\frac{\rho|r|}{3\varepsilon_0}i_r\)
<終>
また,式(5)で電界\(E_{in}\)を求めましょう。
\(E_{in}=-\frac{\partial}{\partial r}(\frac{\rho a^2}{2\varepsilon_0}-\frac{\rho r^2}{6\varepsilon_0})i_r\)
\(E_{in}=\frac{\rho r}{3\varepsilon_0}i_r\)
<終>
電界の発散~ポワソン方程式の導出
そもそも,発散とはどういう意味でしょうか?
発散は,湧きだしや吸い込みを表します。
つまり,電界の発散は,電界の湧きだしや吸い込みを表すことになります。
ちなみに電界\(E\)の発散は,次のような方程式で表されることが知られています。
$$∇・E=\frac{\rho}{\varepsilon}\tag{6}$$
この式は,電荷が電界を吐き出したり吸い込んだりするものであると言うことを意味します。
電荷密度が0のとき,式(6)は,
$$∇・E=0$$
となります。つまり,この式は,電界を吐き出したり吸い込んだりする穴が存在しないことを意味します。
話は変わりますが,式(6)をもう少し突き詰めましょう。電界\(E\)を直交座標表示で表すと,
\(E=E_xi_x+E_yi_y+E_zi_z\tag{7}\)
と表すことができます。式(6)に式(7)と式(3)を代入すると,
\((\frac{\partial }{\partial x}i_x+\frac{\partial }{\partial y}i_y+\frac{\partial}{\partial z}i_z)・( E_xi_x+E_yi_y+E_zi_z)=\frac{\rho}{\varepsilon}\)
$$\frac{\partial }{\partial x}E_x+\frac{\partial }{\partial y}E_y+\frac{\partial}{\partial z}E_z=\frac{\rho}{\varepsilon}\tag{8}$$
電界を求める式同様に難しいですね。
だが,しかーし,対称性のある電界であれば,式(6)はもう少し簡単に表すことができます。
$$\frac{\partial}{\partial r}E_r=\frac{\rho}{\varepsilon}\tag{9}$$
式(8)よりも式(9)の方が簡単ですよね。
電界の発散を計算
電荷密度\(\rho\)[C/m^3],誘電率\(\varepsilon\)[F/m]の空間を囲むガウス面を考えると,ガウスの法則より
$$\oint_{S1}E・dS=\frac{1}{\varepsilon}\int_{V}\rho dV$$
ここで,上の式の左辺にガウスの発散を適用すると,
\(\int_{V}∇・EdV=\int_{V}\frac{\rho}{\varepsilon}dV\)
\(\int_{V}\underbrace{∇・E-\frac{\rho}{\varepsilon}}_{=0}dV=0\)
よって,
$$∇・E=\frac{\rho}{\varepsilon}$$
となって,式(6)が示されました。
ポワソン方程式
ポワソン方程式は次のように表されます。
$$∇・(∇\phi)=-\frac{\rho}{\varepsilon}\tag{10}$$
式(10)は,式(6)に式(2)を代入することで得られます。
ガウス面内に電荷が存在しない場合,式(10)は
$$∇・(∇\phi)=0\tag{11}$$
と書けます。
ポワソン方程式:例題
例題3:
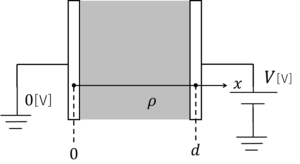
次の図のように,電荷密度\(\rho\)[C/m^3],両極版間に電圧\(V\)[V]を与えます。続いて,\(x=0\)で接地(アース)します。また,真空の誘電率\(\varepsilon_0\)[F/m]のとき,以下の問に答えなさい。
(1) 電荷密度を\(\rho=0\)[C/m^3]としたときの電界\(E\)と電位\(V(x)\)を求めましょう。
(2) 電荷密度が\(\rho\)[C/m^3]のときの電界\(E\)と電位\(V(x)\)を求めましょう
例題3(1)解答->
まず,電位\(V(x)\)を求めましょう。ポワソンの方程式を用いると,\(V(x)\)は,
\(\frac{d^2}{dx^2}V(x)=0\)
次に,両辺を2回だけ不定積分します。
\(\frac{d}{dx}V(x)=C_1\)
\(V(x)=C_1x+C_2\)
ここで,境界条件を使います。
\(V(0)=0\),\(V(d)=V\)
\(V(0)=C_2=0\)
\(V(d)=C_1d=V\)
\(C_1\)は,
\(C_1=\frac{V}{d}\)
よって,電位\(V(x)\)は
\(V(x)=\frac{V}{d}x\)
また,電界\(E\)は,図から\(x\)軸方向しか働かないので,式(8)を適用すると,
\(E=\frac{d}{dx}V(x)i_x\)
\(E=\frac{d}{dx}\frac{V}{d}xi_x\)
\(E=\frac{d}{dx}\frac{V}{d}i_x\)
<終>
例題3(2)解答->
まず,電位\(V(x)\)を求めます。
ポワソン方程式を用いると,\(V(x)\)は,
\(\frac{d^2}{dx^2}V(x)=-\frac{\rho}{\varepsilon_0}\)
両辺を\(x\)で2回だけ不定積分します。
\(\frac{d}{dx}V(x)=-\frac{\rho}{\varepsilon_0}x+C_1\)
\(V(x)=-\frac{1}{2}\frac{\rho}{\varepsilon_0}x^2+C_1x+C_2\)
つぎに,\(C_1\)と\(C_2\)を求めていきます。
ここで,境界条件を使います。図から,
\(V(0)=0\),\(V(d)=V\)なので,
\(V(0)=C_2=0\)
\(V(d)=-\frac{1}{2}\frac{\rho}{\varepsilon_0}d^2+C_1d=V\)
\(C_1\)は,
\(C_1=\frac{V}{d}+\frac{\rho}{2\varepsilon_0}d\)
よって,求める電位\(V(x)\)は,
\(V(x)=-\frac{\rho}{2\varepsilon_0}x^2+(\frac{V}{d}+\frac{\rho}{2\varepsilon_0})x\)[V]
次に,電界\(E\)を求めます。
ここで,式(4)を使うと,
\(E=\frac{d}{dx}V(x)i_x\)
\(E=\frac{d}{dx}(-\frac{\rho}{2\varepsilon_0}x^2+(\frac{V}{d}+\frac{\rho}{2\varepsilon_0})x)i_x\)
\(E=\frac{\rho}{\varepsilon_0}x+(\frac{V}{d}+\frac{\rho}{2\varepsilon_0})i_x\)[V/m]
電界電位の相互関係:関連問題
電験1種
前回の電磁気学の記事

次回の電磁気学の記事

電界電位の相互関係:まとめ
電界と電位の関係式
$$\phi=-\int_{\infty}^{B}E・dr$$
$$E=-∇\phi$$
ポワソン方程式
$$∇・(∇\phi)=-\frac{\rho}{\varepsilon}$$
最後に
電界は電位の勾配。電位は電界のベクトル線積分で表されます。余談になりますが,電磁気学のテスト前は,勾配やベクトル線積分の計算を死ぬほどしたものです。この計算になれていたおかげで,初めての電磁気学のテストは乗り切りました。


















