今日は,導体の電気的性質についての記事を執筆しました。
また,練習問題も用意してありますので,最後までご覧ください。
☑接地と静電遮へいについての問題を解けるようになる
導体の4つの電気的性質
電磁気学の問題を解く上で,導体の性質を知ることは大切です。
導体の性質を見ていきましょう。
導体の性質
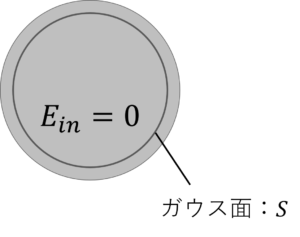
性質1.導体内部の電界は0
性質2.電荷は導体表面のみに存在
性質3.導体の全ての点は同電位
性質4.電界\(E\)は保存場
性質5.電気力線は,互いに交わらない
性質1.導体内部の電界は0

性質2.電荷は導体表面のみに存在
導体内にガウスの法則を適用します。
$$\oint_{S}\underbrace{E}_{=0}・dS=\frac{Q}{\varepsilon}=0$$
導体中の電界は0なので,ガウス面内の電荷も0です。
性質3.導体の全ての点は同電位
導体内の電位差\(\phi\)について,
\(\phi=\int_{A}^{B}\underbrace{E}_{=0}・dr\)
導体内には電界が存在しないので,導体の全ての点は同じ電位になります。

性質4.電界\(E\)は保存場
力\(F\)が保存場なので,電界\(E\)も保存場です。
$$\oint_{c}F・dr=q\oint_{c}E・dr=0$$
性質5.電気力線は,互いに交わらない
電界\(E\)の回転が0であることを意味します。
$$∇\times E=0$$
ちなみに,性質4.と性質5.は同じことを主張しています。ストークスの定理から示すことができます。
静電誘導
導体に電荷を近づけると,近づけた電荷と同じ符号の電荷が現れる現象のことを静電誘導といいました。
詳しくは以下の記事で図をつけて解説しています。

コンデンサと静電容量
静電容量\(C\)は,電荷\(Q\)と電位差\(\phi\)を用いると次式で定義されます。
$$C=\frac{Q}{\phi}\tag{1}$$
単位は,定義からC/Vですが,これをF(ファラド)とします(C/V=F)。
例題1
極板の面積\(S\),極板間の距離\(d\),真空の誘電率を\(\varepsilon_0\)の平行平板コンデンサの静電容量を求めましょう。ただし,端効果はないものとします。
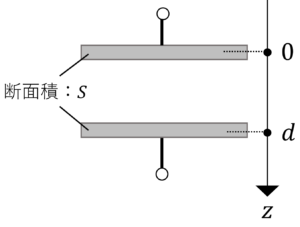
ヒント:仮想的に電荷\(Q\)を上極板に与えます。
例題1解答―>
まず,上極板と下極板にガウスの法則を適用しましょう。
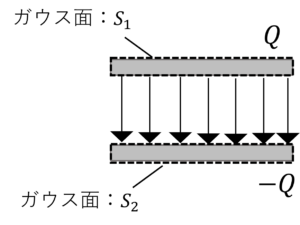
すると,上極板が作る電界は\(E_1\)は,ガウスの法則より
\(\oint_{S_1}E_1・dS=\frac{Q}{\varepsilon_0}\)
\(|E_1|\underbrace{\oint_{S_1}dS}_{2S}=\frac{Q}{\varepsilon_0}\)
\(E_1=\frac{Q}{2\varepsilon_0 S}i_z\),(\(z>0\))
同様に,下極板が作る電界\(E_2\)は,ガウスの法則より
\(E_2=\frac{Q}{2\varepsilon_0 S}i_z\),(\(z<d\))
よって,極板間の電界\(E\),(\0<z<d\)は,
\(E=\frac{Q}{\varepsilon_0 S}i_z\)[V/m]
上極板と下極板の電位差\(\phi\)は,
\(\phi=-\int_{d}^{0}\frac{Q}{\varepsilon_0 S}i_z・i_zdz\)
\(\phi=\frac{Qd}{\varepsilon_0 S}\)[V]
よって,平行平板コンデンサの静電容量\(C\)は,
\(C=\frac{Q}{\phi}=\frac{\varepsilon_0 S}{d}\)[F]
コンデンサの直列接続,並列接続
直列接続
2つのコンデンサを直列に接続します。2つのコンデンサの静電容量をそれぞれ\(C_1\),\(C_2\)とするとき,静電容量\(C\)を計算しましょう。
\(C=\frac{Q}{\phi_1+\phi_2}\)
ここで,両辺の逆数をとります。
\((\frac{1}{C})^{-1}=(\underbrace{\frac{\phi_1}{Q}}_{\frac{1}{C_1}}+\underbrace{\frac{\phi_2}{Q}}_{\frac{1}{C_2}})^{-1}\)
元に戻すと,静電容量\(C\)は,
\(C=(\frac{1}{C_1}+\frac{1}{C_2})^{-1}\)[F]
となります。
並列接続
2つのコンデンサを並列に接続します。2つのコンデンサの静電容量をそれぞれ\(C_1\),\(C_2\)とするとき,静電容量\(C\)を計算しましょう。
\(C=\frac{Q_1+Q_2}{\phi}=\underbrace{\frac{Q_1}{\phi}}_{C_1}+\underbrace{\frac{Q_2}{\phi}}_{C_2}\)
よって,静電容量\(C\)は,
\(C=C_1+C_2\)[F]
コンデンサ:演習問題
半径\(a\),電荷密度\(\rho\)[C/m^3]の球状電荷群がある。真空の誘電率が\(\varepsilon_0\)[F/m]のとき以下の問に答えなさい。
(1) 球状電荷群から\(r\)\((r\leq a)\)離れた点における電界\(E\)と電位\(\phi\)
(2) 球状電荷群の単位体積当たりの静電容量\(C\)
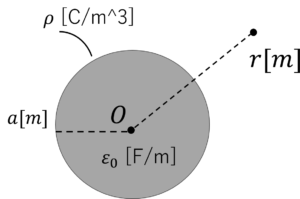
演習問題解答
(1) 解答
電界\(E\)について,
半径\(r\)の球状がウス面をとると,ガウスの法則より,
\(\oint_{S}\underbrace{E}_{|E|i_r}・dS=\int_{V}\frac{\rho}{\varepsilon_0}dV\)
\(|E|\underbrace{\oint_{S}dS}_{4\pi r^2}=\frac{\rho}{\varepsilon_0}\underbrace{\int_{V}dV}_{\frac{4}{3}\pi a^3}\)
\(|E|=\frac{\rho a^3}{3\varepsilon_0 r^2}\)
よって,電界\(E\)は,
\(E=\frac{\rho a^3}{3\varepsilon_0 r^2}i_r\)[V/m]
続いて,電位\(\phi\)を求めます。
\(\phi=-\int_{\infty}^{r}\underbrace{E}_{|E|i_r}・i_rdr\)
\(\phi=-\int_{\infty}^{r}\frac{\rho a^3}{3\varepsilon_0 r^2}dr\)
\(\phi=[\frac{\rho a^3}{3\varepsilon_0 r}]_{\infty}^{r}\)
よって,求める電位\(\phi\)は
\(\phi=\frac{\rho a^3}{3\varepsilon_0 r}\)[V]
(2) 解答
単位体積当たりの静電容量\(C\)は,
\(C=\frac{\rho}{\phi}\)
で求められる。よって,単位体積当たりの静電容量\(C\)は,
\(C=\frac{3 \varepsilon_0 r}{a^3}\)[F/m^3]
コンデンサ:関連問題
電験1種
電験2種
電験3種
前回の電磁気学の記事

次の電磁気学の記事

導体とコンデンサ:まとめ
静電容量\(C\)を電位差\(\phi\),電荷\(Q\)で表すと,
$$C=\frac{Q}{\phi}$$
コンデンサの静電容量\(C\)
$$C=\varepsilon_0\frac{S}{d}$$
直列接続したコンデンサの合成静電容量\(C\)
$$C=(\frac{1}{C_1}+\frac{1}{C_2})^{-1}$$
並列接続したコンデンサの合成静電容量\(C\)
$$C=C_1+C_2$$
最後に
電磁気学のテストの3日前にこの記事を執筆しました。万が一単位を落としたら,ショックで気絶不可避です。私は,電験2種の理論は合格点だったわけだし,単位くらい楽にとらせて欲しいと切に願っています。