今日の記事は,電束密度に関する記事です。
この記事を読むメリット
☑電束密度に関するガウスの法則を使えるようになる
☑電束密度が出てくる問題を解けるようになる
電束密度の定義式
今日の記事を読みに来てくださった皆さんを,以下の誘電体の内部電界\(E\)を導出できるようにします。
さて,この問題をスマートに解く為に新たな物理量を伝授しましょう。
それが,電束密度\(D\)[Q/m^2]です。
電束密度\(D\)の2つの公式
よく用いられる電束密度\(D\)の関係式を2式ほどご紹介します。
電束密度\(D\)と電界\(E\)の関係式
$$D=\varepsilon E \tag{1}$$
\(\varepsilon\):物質中の誘電率
\(\varepsilon_0\)は,真空の誘電率を表すのに対して,\(\varepsilon\)は,物質中の誘電率を表します。
ここで,式(1)を\(\varepsilon_0\)を用いて表してみると,
$$D=\varepsilon_0 \varepsilon_r E \tag{1’}$$
\(\varepsilon_0\):真空の誘電率
\(\varepsilon_r\):比誘電率
比誘電率\(\varepsilon_r\)は一体何者なのでしょうか?
比誘電率\(\varepsilon_r\)は,\(\frac{\varepsilon}{\varepsilon_0}\)で表されることから,真空中の誘電率から見た物質中の誘電率の大きさという意味になります。
ちなみに,比誘電率\(\varepsilon_r\)が定義された理由は,
物質の誘電率\(\varepsilon\)が小さすぎるからという理由らしいです。
例えば,真空の誘電率\(\varepsilon_0\)は,\(\varepsilon_0=8.854×10^{-8}\)くらいでものすごく小さいです。
誘電率の値を実験中にやりとりすることをイメージしてください。
\(10^{-7}\)くらいの小さなスケールで話されると困りますよね?
比誘電率\(\varepsilon_r\)であれば,スケールが1,10,100くらいの大きさなので,ストレスを感じにくいと思います。
電束密度\(D\),電荷\(Q\)の関係式
$$\oint_S D・ndS=\sum Q \tag{2}$$
私たちは,以前,電界に関するガウスの法則を学んでいます。
なので,電束密度のガウスの法則(式(2))はいらないのではないか?
と考える人がいるかもしれませんね。
でも,実は,電束密度のガウスの法則は電界密度のガウスの法則に比べて,万能な公式なんです。それを今から説明していきます。
電界\(E\)のガウスの法則に関する記事->


まず,電界\(E\)のガウスの法則は,
$$\oint_S E・ndS=\frac{1}{\varepsilon}\sum Q\tag{2’}$$
\(\varepsilon\):誘電率
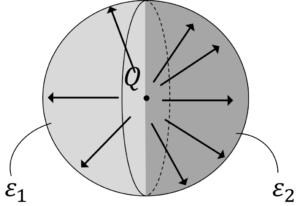
でした。この式(2’)から,下の図の内部電界\(E\)を求めることができますか?



図1.場所ごとに誘電率が違う誘電体
おそらく,電磁気学初学者の方はこの問題で躓くと思います。
半径\(r\)の球状のガウス面をとった場合,
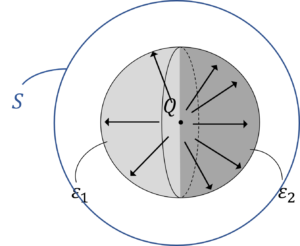
図2.半径\(r\)の球状ガウス面
このようになって,場所ごとに誘電率\(\varepsilon\)が違うので,解けません。
ちなみに,正しいガウス面の取り方は,
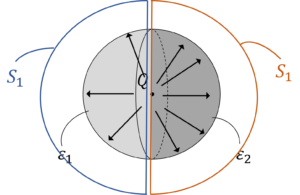
図3.半径\(r\)の半球状ガウス面をとる
このようにガウス面をとれば,解くことができますが,スマートではありません。
図2のガウス面でスマートに解く方法はあるのでしょうか?
実は,電束密度に関するガウスの法則を使うとうまくいきます。

\(\oint_{S}\underbrace{D}_{|D|i_r}・dS=Q\)
\(|D|\underbrace{\oint_{S}dS}_{4\pi r^2}=Q\)
\(|D|=\frac{Q}{4\pi r^2}\)
となり,電束密度\(D\)は,
\(D=\frac{Q}{4\pi r^2}i_r\)[C/m^2]
となります。更に,左側の電界\(E_{1}\)と右側の電界\(E_{2}\)についてそれぞれ求めると,
\(E_{1}=\frac{Q}{4\pi \varepsilon_1 r^2}i_r \)[V/m]
\(E_{2}=\frac{Q}{4\pi \varepsilon_2 r^2}i_r \)[V/m]
となります。
あれ,左右の誘電体の境界で電界が不連続になっているけれど大丈夫なの?
と思われる方がいらっしゃるかもしれませんが,
電界と電束密度の境界条件の記事をご覧になっていただければわかります。->
電気双極子モーメント
電気双極子モーメント\(p\)は,次式で定義されます。
$$p=qs_{-→+}\tag{4}$$
\(q\):電荷,\(s_{-→+}\):負電荷から見た正電荷の位置ベクトル
電気双極子モーメント\(p\)は,周りに電界がかかると発生します。
例えば,次のような電子模型を考えます。

図4.電界をかけていないときの水素原子の状態
この電子に上向きの電界をかけると,電界と同じ方向に電気双極子モーメントが発生します。

図5.電界をかけたときの水素原子の状態
問題1


図に示す電気双極子モーメント\(p\)が位置\(r\)に作る電位\(\phi\)は,
\(\phi=\frac{p・r}{4\pi \varepsilon_0 |r|^3}\)
であることを示しましょう。ただし,\(s<<r\)とします。
問題1解答
電位\(\phi\)について,
\(\phi=\frac{q}{4\pi \varepsilon_0}(-\frac{1}{|r|}+\frac{1}{|r-s|})\)
ここで,\(s<<r\)より,第2項にスカラー関数の1次のマクローリン展開を適用すると,電位\(\phi\)は,
\(\phi≒\frac{q}{4\pi \varepsilon_0}(-\frac{1}{|r|}+[\frac{1}{|r|}+∇\frac{1}{|r-s|}]_{s=0}・s)\)
と近似できます。
\(=\frac{q}{4\pi \varepsilon_0}([\frac{∂}{∂s}\frac{1}{|r-s|}∇(r-s) ]_{s=0}・s)\)
\(=\frac{q}{4\pi \varepsilon_0}([\frac{1}{|r-s|^2|}\frac{r-s}{|r-s|}]_{s=0}・s)\)
\(=\frac{q}{4\pi \varepsilon_0}[\frac{r}{|r|^3|}・s\)
ここで,\(qs=p\)より,求める電位\(\phi\)は,
\(\phi=\frac{p・r}{4\pi \varepsilon_0 |r|^3}\)[V]
電気分極
誘電体あるところに電気分極あり,
電気分極\(P\)は一般に,以下の式で表されます。
$$D=\varepsilon_0 E+P \tag{3}$$
そして,多くの誘電体では電気分極\(P\)は,電界\(E\)に比例します。
$$P=χE=\varepsilon_0 (\varepsilon_r-1) E\tag{4}$$
\(χ\):電気感受率
ちなみに,式(4)を式(3)に代入すると,
\(D=\varepsilon_0 E+\varepsilon_0 (\varepsilon_r-1) E=\varepsilon_0 \varepsilon_r E\)
となり,電束密度の定義式そのものになります。
では,2つの極板間に電界をかけてみましょう。
2つの極板間に何もない場合は,電気分極\(P\)は発生しません。

しかし,極板間に誘電体を挟むと,中に電気分極\(P\)が発生し,電界\(E\)が小さくなります。
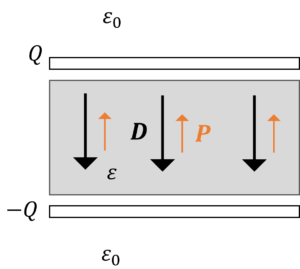

ここで,誘電体内部の電気的な状態を見てみましょう。
誘電体は,電気双極子モーメントの集まりとみなせるので,2つの極板間の誘電体は以下のように表すことができます。
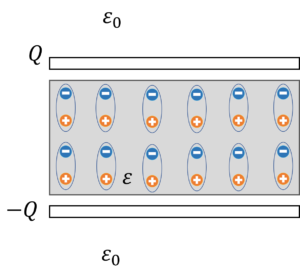

更に,誘電体内部で+とーが打ち消しあうので,


このように,誘電体表面に電荷\(Q_p\)が誘起されます。
また,極板の間にあるのが導体であれば,導体表面に電荷\(Q\)が誘起され,導体内部の電界は0になります。
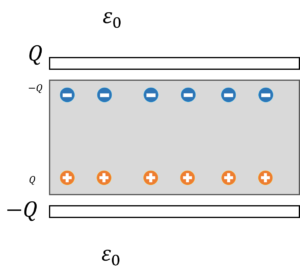

問題2
断面積\(S\)の2つの極板間の誘電率\(\varepsilon\)の誘電体について,電気分極\(P\)を求めましょう。ただし,端効果はないものとします。
問題2解答
まず,電界\(E\)と電束密度\(D\)を求めましょう。
\(E=\frac{Q}{\varepsilon S}\)[V/m]
\(D=\frac{Q}{S}\)[C/m^2]
よって,電気分極\(P\)は,
\(P=D-\varepsilon_0 E=\frac{Q}{S}(1-\frac{\varepsilon_0}{\varepsilon})\)[C/m^2]
電束密度:関連問題
演習問題は以下の記事をご覧くださいー>

電験1種
電験2種
前回の電磁気学


次の電磁気学


電束密度:まとめ
電束密度に関するガウスの法則
$$\oint_{S}D・dS=\sum Q$$
\(D\):電束密度,\(Q\):電荷
電束密度と電界の関係式
$$D=\varepsilon E=\varepsilon_0 \varepsilon_r E$$
\(E\):電界,\(\varepsilon\):誘電率,\(\varepsilon_0\):真空誘電率,\(\varepsilon_r\):比誘電率
電気双極子モーメント\(p\)の定義式
$$p=qs_{-→+}$$
電気双極子モーメント\(p\)と電位\(\phi\)の関係式
$$\phi=\frac{p・r}{4\pi \varepsilon_0 |r|^3}$$
電気分極\(P\),電界\(E\),電束密度\(D\)の関係式
$$D=\varepsilon_0 E+P$$
最後に
電磁気学のテキストを見ると電束密度と電気分極がセットになって出てきます。
でも,私自身,電気分極についてあまり理解していないので,弊記事での解説は控えさせていただきます。


















