今回は、C言語による非線形方程式の解き方などを紹介していくよ!
この記事では、基礎的な事しか書いていないから、アルゴリズムについてもっと良く知りたい方やコードについて知りたい方は、他の記事を参考にして下さい!
非線形方程式
まずは、非線形方程式の解き方について紹介していきたいと思います。
数学に慣れていない人は、非線形方程式とは何だろうと思うかもしれませんが、非線形方程式とは、x^8+x^5+3x^2+9=0やf(x)=x-sinx=0など、一般に解を求める公式が存在しない方程式のことを言います。
逆に言えば、x^2+x+1=0やf(x)=cosx=0等は線形方程式となります。
非線形方程式は公式が存在しないので、解を直接的には求めることが出来ません。
ですので、非線形方程式を求める際には、実際に数値を求めていき、近似的に解を求めなければなりません。
今回は非線形方程式の解法として2分法とニュートン法を紹介していきたいと思います。
2分法
長所:必ず収束する
短所:収束が遅い
説明:
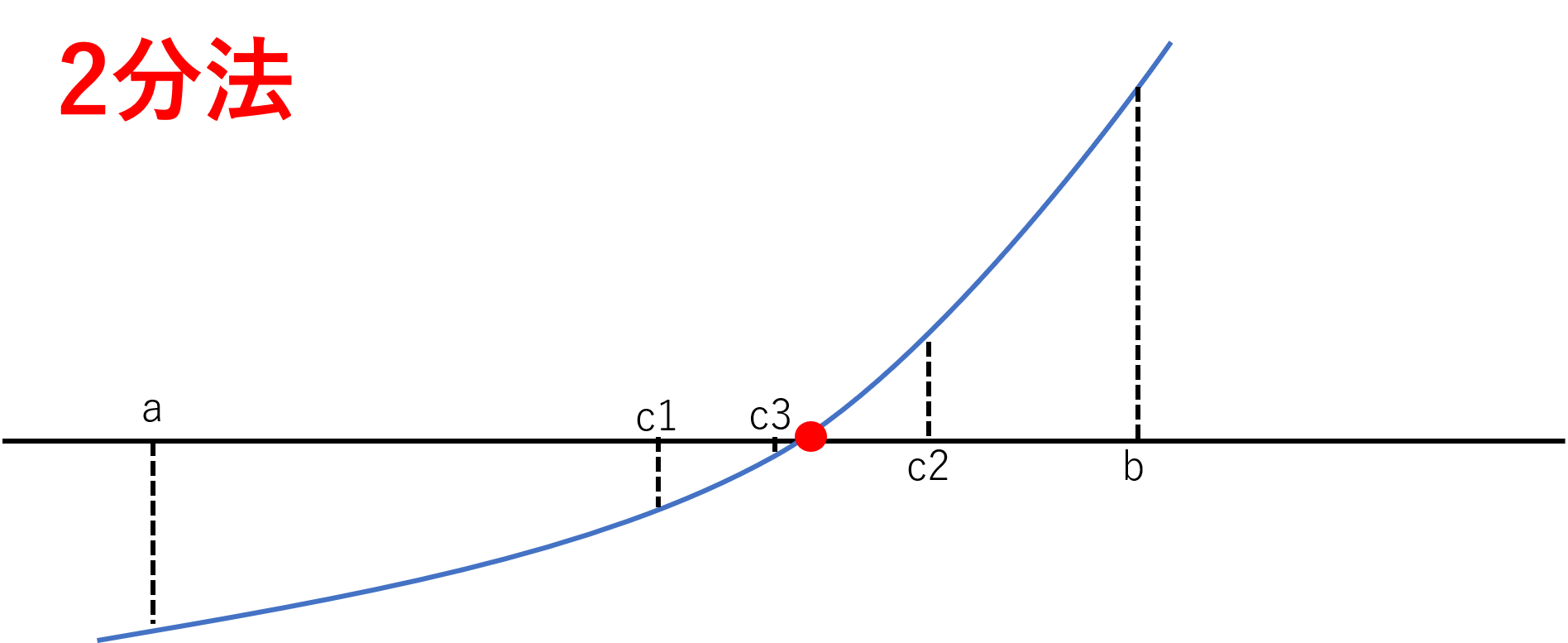
上の図の赤丸を見ながら解説を見てもらうとわかりやすいかと思います。
2分法では、2点間で挟んで処理を開始します。(今回、最初とる値はa,bとする。)
今回の条件では[a,b]内で、解が1つの場合のみ成り立ちます。
この際、a点の値とb点の値の符号がそれぞれ異なっていなければ、その間に0が存在しない事になることが分かります。(例:a=c2とbの場合0は存在しない事が分かる)
もし適当にa,b点を取った場合、この状態がかなりの確率で起こると考えられます。
これを調べる方法は、処理を開始する前に大きくA,Bをとりそれを細かく分割していき確認していきます。
A,Bの間をn個で分割する際、その1個の幅は(B-A)/nとなります。(A<B)
その区間の両端の値を、関数に当てはめ2つの積の値が負の場合その両端をa,bにします。(区間[a,b])
区間[a,b]の中点を求めると、c1が出てきます。
この際、その中点とa,bそれぞれを掛けてみます。ここで先ほど行った作業をもう一度行います。
c1(中点)とa,bどちらかの符号が異なっていれば、そちら側の区間(aとc1の積が負となれば区間[a,c1] bとc1の積が負となれば区間[c1,b])に0(解)が存在するということになります。
次は、積が負になった区間で中点を取っていきます。これを繰り返していくことによって、限りなく0を取る値(解)に近づく事が出来ます。
この限りなくというのは、ほとんど0の値になるのですが、先ほどの作業で各点の半分を取っているんで、これでは0になることはありえません。
ですので、ここではあらかじめ限りなく0に近い値を用意しておく必要があります。
今回用意したコードではepsの部分がそのようになります。
これらをコードで表わすと、以下の様になります。
サンプルコード
ニュートン法
長所:収束が早い
短所:収束は初期値に依存する。収束しない場合がある。
説明:
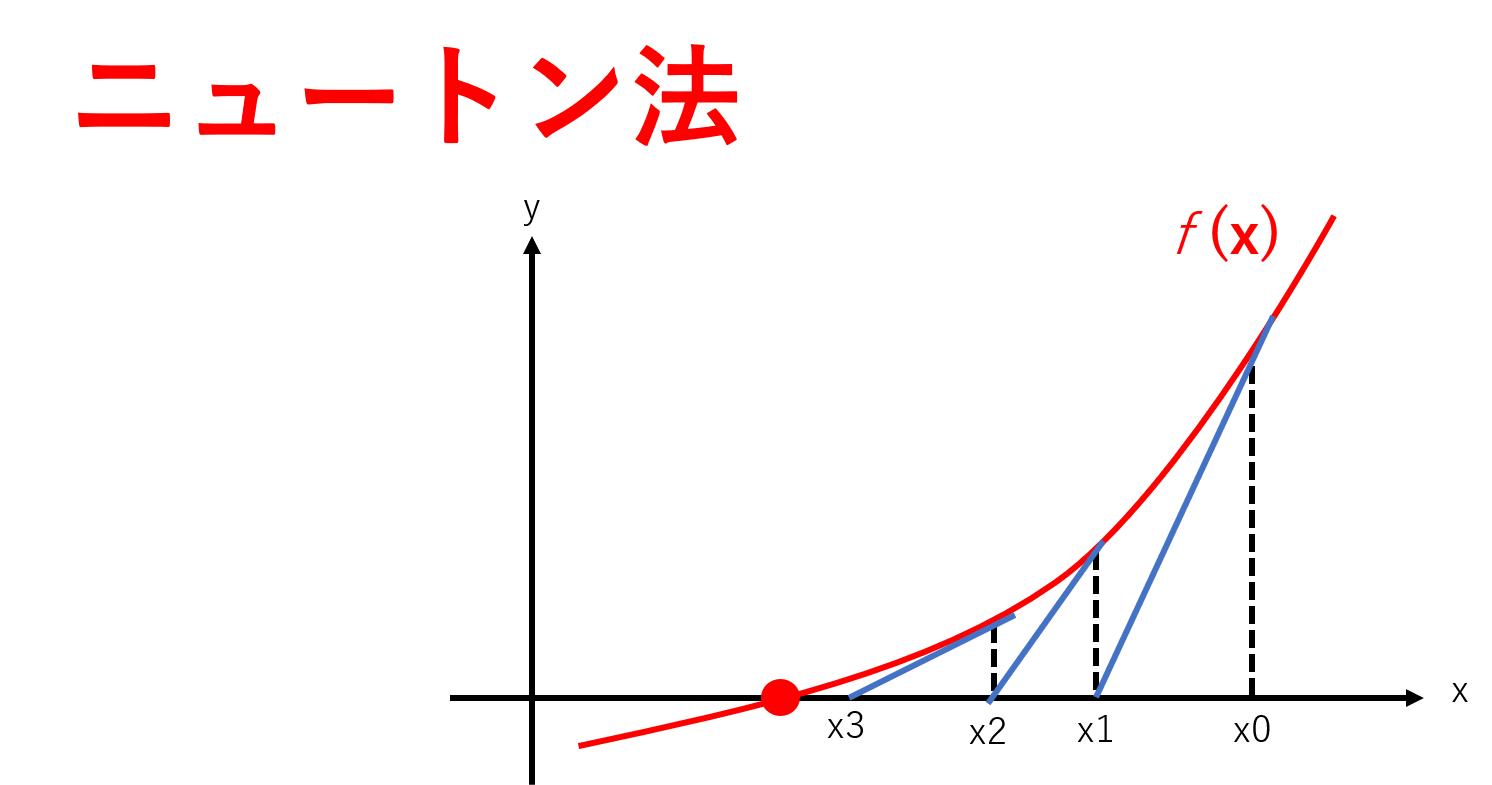
ニュートン法では接線を用いて解を導出していきます。
まずは、初期値(x0)を決めそこの接線の方程式を求めます。
接線の方程式を求めると、y=f’(x0)(x-x0)+f(x0)となります。(この部分は高校数学の範囲なので調べてもらうと、簡単に分かります。)
この接線の方程式がx軸と交わる点(y=0)をx1とすると、0=f’(x0)(x1-x0)+f(x0)をx1について求めると、x1=x0 – f(x0) / f’(x0)となることが分かります。
これを同じように、x1の接線を求めてy=0とし、x2となるものを求めると先ほどと同様のような式が導出されます。
x2=x1 – f(x1) / f’(x1)という式が求められます。
これを繰り返す事により、0になる値(解)が求まります。(上図を見てもらうと分かりやすい)
これがニュートン法となります。
この作業をいつまで繰り返すの?と疑問に思うかと思いますが、今回もある程度小さい値を設定しておき(コード内のEPS)、隣合うxの値の差がその値より小さくなった場合終了します。
しかし、ニュートン法(この作業)ではその特性上、初期値を解になる箇所の近くに置かないと収束しない場合(小さい値などが関係なくなる)があります。
この場合は、プログラム内では解はないと判断して終了させる必要があります。
この対策としては、試行回数に制限をかける必要があります。
ニュートン法では、収束しない場合を考慮する必要があるので、初期値を取る際には少し考える必要があるので気を付けて下さい。
ここで出てくる、微分ですが今回はあらかじめ関数の微分は分かってるものとしているので、注意して下さい。
サンプルコード
最後に
今回は、非線形方程式の解法について紹介してきました。
非線形方程式の解き方で、代表的な2分法とニュートン法を行ってきましたがやっていることは意外と簡単なものなので、慣れるとコードの意味が簡単に分かると思います。
ぜひ、1回で分からない場合は、複数回コードなどを見直してみて下さい。
今回はこれで以上になります。
最後まで読んでいただきありがとうございました!


















