プログラミングでお金を稼ぎたい。どうも,ユキです。
今回は,電気学の集大成もかねて演習問題を3題程用意しました。私の拙い解答付きですが,ご自愛ください。
この記事を読むメリット
☑電気学の応用問題を解くことができる
問題1
無限に広がる接地導体に対して垂直に距離\(d\)[m]離れた位置に,半径\(a\)[m]の微小球があるとする。微小球は,正電荷\(+Q\)[C]に帯電しているとして,以下の問いに答えよ。
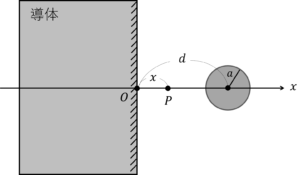
1) 導体を無視して微小球から距離\(r\)[m]\(a≪r\)の点\(P’\)における電界\(E_r\)の大きさを求めよ。
2) 導体を考え,日昇級と導体の間で導体からの距離\(x\)[m]の点における電界\(E\)を求めよ。
3) 導体と微小球の間の電位差\(V\)を求めよ。
4) 導体と微小球の間の静電容量\(C\)を求めよ。
問題1解答
(1)解答
半径\(r\)の球状ガウス面をとると,ガウスの法則より
\(\oint_{S}\underbrace{E_r}_{|E_r|i_r}・dS=\sum \frac{Q}{\varepsilon_0}\)

図1.半径\(r\)のガウス面
\(|E_r|\underbrace{\oint_{S}dS}_{4\pi r^2}= \frac{Q}{\varepsilon_0}\)
\(|E_r|=\frac{Q}{4\pi \varepsilon_0 r^2}\)
よって,求める電界\(E_r\)は,
\(E_r=\frac{Q}{4\pi \varepsilon_0 r^2}i_r\)[V/m]
<終>
電界に関するガウスの法則が分からない方ー>

(2)解答
影像電荷を考える。
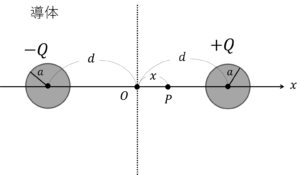
図2.影像法
求める電界\(E\)は,(1)を踏まえると,
\(E=\underbrace{-\frac{Q}{4\pi \varepsilon_0 (d-x)^2}i_x}_{+Qが作り出す電界}-\underbrace{\frac{Q}{4\pi \varepsilon_0 (d+x)^2}i_x}_{-Qが作り出す電界}\)
\(E=-\frac{Q}{4\pi \varepsilon_0}(\frac{1}{(d-x)^2}+\frac{1}{(d+x)^2})i_x\)[V/m]
(3)解答
電位差\(V\)について,
\(V=-\int_{C}E・dr=\int_{0}^{d-a}\frac{Q}{4\pi \varepsilon_0}(\frac{1}{(d-x)^2}+\frac{1}{(d+x)^2})\underbrace{i_x ・i_x}_{1}dx\)
\(V=\frac{Q}{4\pi \varepsilon_0}[(\frac{1}{d-x}-\frac{1}{d+x})]_{0}^{d-a}\)
\(V=\frac{Q}{4\pi \varepsilon_0}(-\frac{1}{2d-a}+\frac{1}{a})\)
よって,求める電位差\(V\)は,
\(V=\frac{Q}{2\pi \varepsilon_0}(\frac{d-a}{a(2d-a)}\) [V]
(4)解答
静電容量\(C\)は,
\(C=\frac{Q}{V}=\frac{2\pi\varepsilon_0 a(2d-a)}{d-a}\)[F]
問題2
図のような縦\(a\)[m],横\(b\)[m]の長方形の極板を持つ真空中の平行板コンデンサに極板間隔\(d\)[m]と同じ厚さの誘電体板が幅\(x\)[m]挟まっている。端効果は無視し,真空の誘電率を\(\varepsilon_0\)[F/m],誘電体板の誘電率を\(\varepsilon\)[F/m]として以下の問に答えよ。ただし,\(0<\varepsilon_0<\varepsilon\)とする。
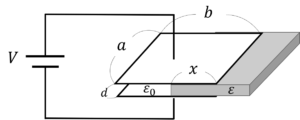
1) 平行板コンデンサの静電容量を求めよ。
2) このコンデンサに電圧\(V\)[V]を印加したとき,このコンデンサに蓄えられる静電エネルギーはいくらか?
3) 2)の場合に誘電体板がコンデンサに引き込まれる力の大きさを求めよ。
問題2解答
(1)解答
平行板コンデンサの静電容量\(C\)は,
\(C=\frac{\varepsilon_0 a(b-x)+\varepsilon_0 ax}{d}\)[F]
(2)解答
蓄えられる静電エネルギー\(U\)は,
\(U=\frac{1}{2}CV^2=\frac{\varepsilon_0 a(b-x)+\varepsilon_0 ax }{d}V^2\)
(3)解答
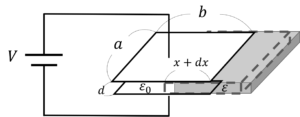
図3.コンデンサ内に引き込まれる誘電体
\(x\)を\(dx\)だけ内側にずらすと仮定すると,
\(F=\frac{dU}{dx}|_{V=const}\)
より,
\(F=\frac{\varepsilon a-\varepsilon_0 a}{d}V^2\)
\(\varepsilon_0 \)よって,力\(F\)は,コンデンサに引き込まれる向きに,
\(\frac{aV^2}{d}(\varepsilon-\varepsilon_0)\)[N]。
問題3
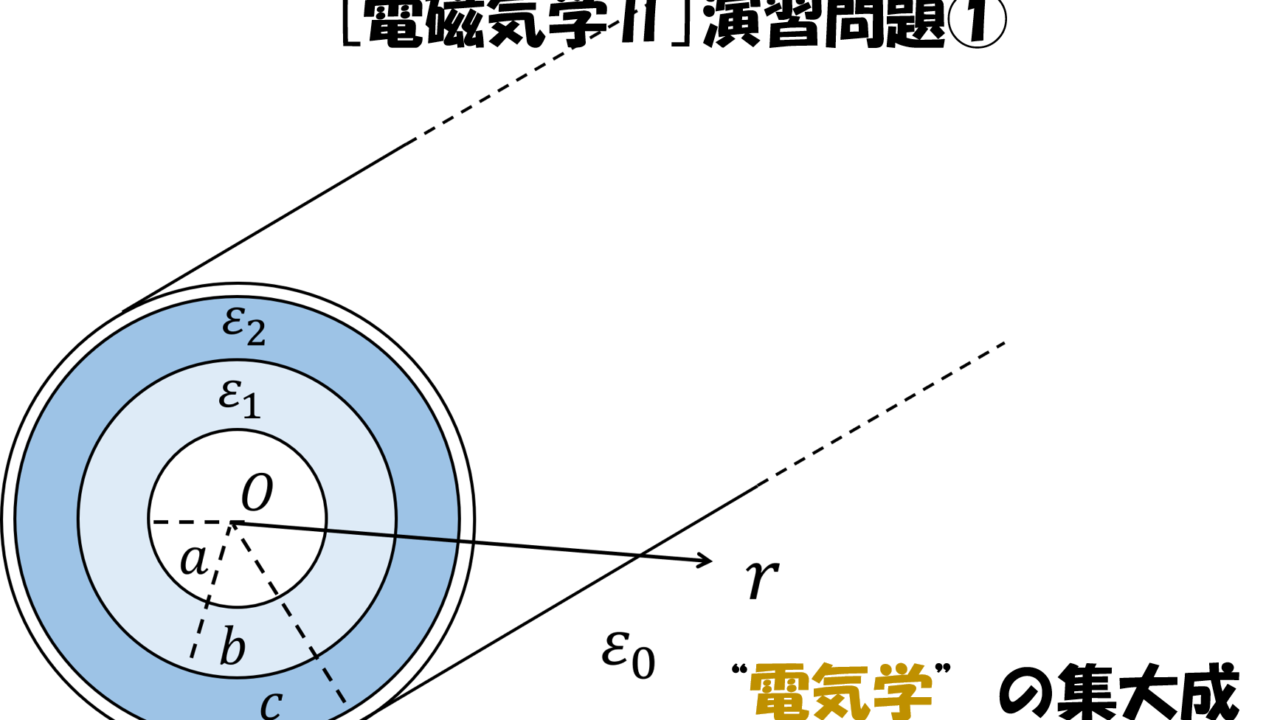
右図に示すような無限に長い同軸ケーブルの内導体と外導体の間が2種の誘電率\(\varepsilon_1\),\(\varepsilon_2\)をもつ誘電体で同心円筒状に満たされているとき,下記の問に答えよ。ただし,内導体(半径\(a\)[m])に単位長あたり\(+λ\)[C/m],外導体に単位長あたり\(-λ\)[C/m]の電荷を与え電荷は長さ方向には一様に分布しているものとする。
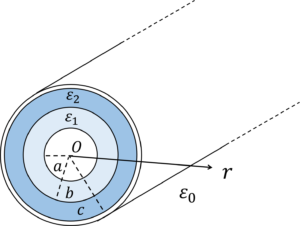
1) \(\varepsilon_1\),\(\varepsilon_2\)各媒質中の電界\(E_1\),\(E_2\)の大きさを求めよ。
2) \(\varepsilon_1\),\(\varepsilon_2\)各媒質中の電束密度\(D_1\),\(D_2\)の大きさを求めよ。
3) 外側と内側の導体間の電位差\(V\)を求めよ。
4) 単位長さあたりの静電容量\(C\)を求めよ。
5) 誘電体界面に働く単位面積あたりの力の大きさ\(f\)を求めよ。\(f\)の向きは図示せよ。
問題3解答
(1),(2)解答
半径\(r\)のガウス面をとると,電束密度に関するガウスの法則より,
\(\oint_{S}\underbrace{D}_{|D|i_r}・dS=\sum Q\)
\(|D|\underbrace{\oint_{S}dS}_{2\pi rh}=λh\)
\(|D|=\frac{λ}{2\pi r}\)
よって,電束密度\(D_1,D_2\)は,
\(D_1=D_2=\frac{λ}{2\pi r}\)[C/m^2]
また,電界\(E_1,E_2\)は,
\(E_1=\frac{D_1}{\varepsilon_1}=\frac{λ}{2\pi r\varepsilon_1}\)[V/m]
\(E_2=\frac{D_2}{\varepsilon_2}=\frac{λ}{2\pi r\varepsilon_2}\)[V/m]
(3)解答
\(V=-\int_{c}^{a}E・dr=-int_{c}^{b}\underbrace{E_2}_{\frac{λ}{2\pi r\varepsilon_2}}・dr-int_{b}^{a}\underbrace{E_1}_{\frac{λ}{2\pi r\varepsilon_1}}・dr\)
\(V=-\frac{λ}{2\pi}(\frac{[\log r]_{c}^{b}}{\varepsilon_2}-\frac{[\log r]_{b}^{a}}{\varepsilon_1})\)
よって,電位差\(V\)は,
\(V=\frac{λ}{2\pi}(\frac{\log \frac{c}{b}}{\varepsilon_2}+\frac{\log \frac{b}{a}}{\varepsilon_1})\)[V]
(4)解答
単位長さあたりの静電容量Cは,
\(C=\frac{λ}{V}=\frac{2\pi\varepsilon_1\varepsilon_2}{\varepsilon_1 \log \frac{c}{b}+\varepsilon_2 \log \frac{b}{a}}\)[F/m^3]
(5)解答
誘電体界面に働く単位面積あたりの力の大きさ\(f\)について,誘電体界面\(r=b\)を\(dr\)だけ短くすると仮定した場合,単位体積当たりのエネルギー\(w\)を用いて,
\(f=-w|_{Q=const}\)
とかける。
\(W=\frac{λ^2}{C}=\frac{λ^2}{2\pi \varepsilon_1 \varepsilon_2}(\varepsilon_1 \log \frac{c}{b}+\varepsilon_2 \frac{b}{a})\)
\(f=-\frac{λ^2}{C}=\frac{λ^2}{2\pi \varepsilon_1 \varepsilon_2}(\varepsilon_1 \log \frac{c}{b}+\varepsilon_2 \frac{b}{a})\)
よって,力\(f\)は,内側に引き込まれる向きに\(\frac{λ^2}{2\pi \varepsilon_1 \varepsilon_2}(\varepsilon_1 \log \frac{c}{b}+\varepsilon_2 \frac{b}{a})\)[N/m^2]。
まとめ
最後に
弊サイトが大学中に知れ渡ることを密かに期待している。