電界と電束密度の境界条件

ユキ

どうも，ユキです。

今日は，電界と電束密度の境界条件についてお話しします。

大学院試でよく出てくるので，押さえておくことが賢明だと思います。

この記事を読むメリット
☑電界と電束密度の境界条件について学べる
☑境界条件をベクトルで考えることで，記憶を定着させることができる

電界の境界条件

電界$E$は，境界面に垂直なベクトル$n$を用いて表すと，

$$E_1×n=E_2×n\tag{1}$$

ここで，×はベクトルの外積を表しています。

式(1)を高校生でもわかるように書くと，

$$|E_1|\sin \theta_1=|E_2|\sin \theta_2\tag{1’}$$

と変形出来ます。

この式(1)，(1’)は2つのことを主張しています。

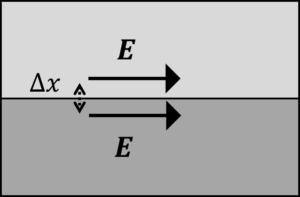
まず，電界は，境界面に平行な方向で連続であるということがいえます。

また，境界面と垂直な方向は，連続でなくても構いません。

電束密度の境界条件

前回の記事で，電束密度についてのお話を取り上げました

電束密度と電気双極子モーメントについて電束密度，電気分極，電気双極子モーメントなどの物理量をご存じでしょうか？これを知ることで，物質の中の電気的性質がより鮮明に浮かび上がってくるでしょう。また，これらに関する電気主任技術者試験の問題へのリンクを貼っているので，勉強用として活用してください。...

電束密度$D$は，境界面に垂直なベクトル$n$を用いて表すと，

$$D_1･n=D_2･n\tag{2}$$

ここで，･はベクトルの内積を表しています。

高校生でもわかるように式(2)を書き換えると，

$$|D_1|\cos \theta_1=|D_2|\cos \theta_2\tag{2’}$$

式(2)，(2‘)は，先ほど同様に2つのことを主張しています。

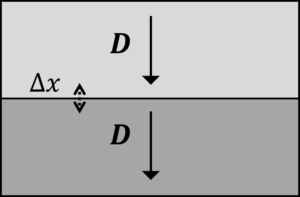
電束密度は，境界面に垂直な方向で連続であるということがいえます。

また，境界面と平行な方向は連続でなくてもいいということです。

電束密度電界の境界条件を導出！

式(1)，式(2)の導出は，式の本質を理解したいという方，また，公式を覚えたくないという方のみご参照ください。あと，高校物理程度の知識では絶対に理解出来ないような導出になっています。

電界の境界条件の導出

式(1)を導出しましょう。

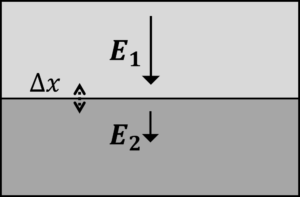
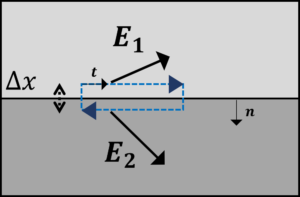
まずは，下の図のように境界面をまたぐように，周回積分しましょう。

すると，電界$E$の周回積分は，エネルギー保存則より

$\int_{C}E･dr=0$

※$r$は位置ベクトル
※$t$は境界面に平行なベクトル

となります。式を変形していきましょう。

$\oint_{C}E･tdr=0$

$\int_{C’}E_1･t dr-\int_{C’}E_2･t dr=0$

積分を外すと，

$E_1･t-E_2･t=0$

$E_1･t=E_2･t$

$E_1×n=E_2×n$

※$n$は境界面に垂直な単位ベクトル

となり，電界に関する境界条件を求めることができました。

電束密度の境界条件の導出

式(2)を導出しましょう。

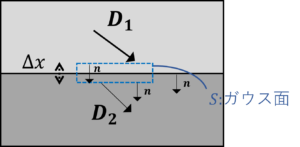
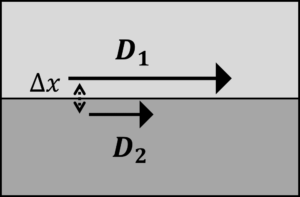
上の図のように境界面に電束密度に関するガウスの法則を適用すると，

$\oint_{S}D･dS=\sum Q=0$

$\oint_{S}D･dS=0$

$\oint_{S}D･ndS=0$

※$S$は面を表す面ベクトル
※$n$は境界面に垂直な単位ベクトル

更に式変形をすると，

$\int_{S’}D_1･ndS-\int_{S’}D_2･ndS=0 $

積分を外すと，

$D_1･n=D_2･n$

ということで式(2)を導出できました。

電束密度電界の境界条件：例題

例題1

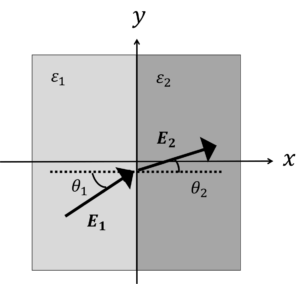
図のように，誘電率が$\varepsilon_1$と$\varepsilon_2$の2種類の誘電体が平行に接している。このとき，電界$E_1$が境界面に入射角$\theta_1$で入射するとき，

(1) 電界$E_1$，電束密度$D_1$をベクトル表示で表しましょう。
(2) 電界$E_2$，電束密度$D_2$を$E_1$，$\theta_1$，$\varepsilon_2$を用いて表しましょう。
(3) $\theta_2$を$\theta_1，\varepsilon_1，\varepsilon_2$を用いて表しましょう。