[電磁気学]電気影像法(鏡像法)で電界を求める

$$\require{\cancel}$$

ユキ

人事を尽くして天命を待つ。どうも，ユキです。

今日は，鏡像法についてのお話です。

この記事を読むメリット
☑影像法(鏡像法)を利用して，電界，電位を求めることができるようになる。

半無限接地導体の影像法(鏡像法)

下の図のように,半無限接地導体があるときの点$P$の電界について考えてみましょう。

図1．半無限接地導体と点電荷

この問題は,点$(-a, 0)$に影像電荷$-Q$を仮定することで,点$(x,　y)$における電界

を求めることができるようになります。

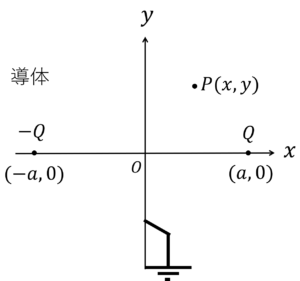
図1．半無限接地導体と点電荷

では，早速ですが，この図を利用して例題を解いていただきましょう。

例題

点$(a，0)$に点電荷$Q$をおき，$x=0$で，無限導体を接地した。このとき，影像法を用いて，点$P$における電界を求めなさい。

例題解答

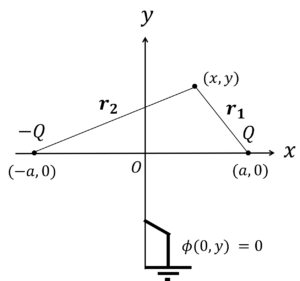
鏡像法を適用すると,次のように図を書き換えられます。

点電荷$Q$が作る電界$E_1$について，

半径$r$のガウス面を取ります。

点電荷に対して，ガウスの法則を適用すると，

$\oint_{S}\underbrace{E_1}_{|E_1|i_r}･i_rdS=\frac{Q}{\varepsilon_0}$

$|E_1|\underbrace{\oint_{S}dS}_{4\pi r_1^2}=\frac{Q}{\varepsilon_0}$

$|E_1|=\frac{Q}{4\pi r_1^2 \varepsilon_0}$

$E_1=\frac{Q}{4\pi r_1^2 \varepsilon_0}i_r $

$E_1=\frac{Q}{4\pi \varepsilon_0 (\sqrt{(x-a)^2+y^2})^3}(x-a，y)$

影像電荷$-Q$が作る電界$E_2$も同様に計算すると，

$E_2=-\frac{Q}{4\pi r_2^2 \varepsilon_0}i_r $

$E_2=-\frac{Q}{4\pi \varepsilon_0 (\sqrt{(x+a)^2+y^2})^3}(x+a，y)$

よって，求める電界$E$$(=E_1+E_2)$は，

$E=\frac{Q}{4\pi \varepsilon_0}(\frac{1}{((x-a)^2+y^2)^{\frac{3}{2}}}(x-a，y)-\frac{1}{((x+a)^2+y^2)^{\frac{3}{2}}}(x+a，y))$

2種類の誘電体における影像法

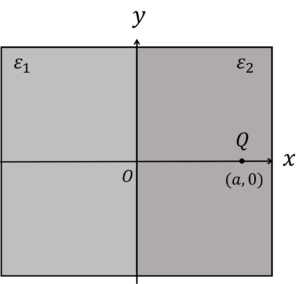
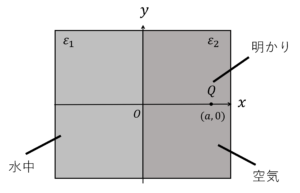
図4．2種類の誘電体＋点電荷

図4のような,左半分は誘電率$\varepsilon_1$，右半分は誘電率$\varepsilon_2$の物質で覆われる2種類の誘電体の$(x,　0)$の位置に点電荷$Q$を配置したときの任意の点$(x, y)$における電界を求めてみましょう。

この問題も鏡像法で解けますが、先ほどよりやや複雑です。

この場合は$x \leq 0$と$x \geq 0$に場合分けをして考えます。

図4を浴槽に水を張った，1つの明かりがある風呂場に置き換えながら説明します。

(ⅰ)　$x \leq 0$のとき

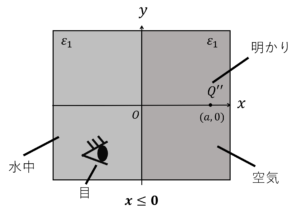
$x \leq 0$のとき，鏡像法より

となります。

これは,　例えるなら,水の中から見た光源のイメージです。

水の中から水の外の明かりを見れば，ぼやけて見えるでしょう。

影像電荷が$Q^{‘’}$なのは，点電荷$Q$が作り出す電界のうち,　一部の電界しか境界面を透過しないからです。

(ⅱ)　$x \geq 0$のとき

$x \geq 0$のとき，鏡像法より,

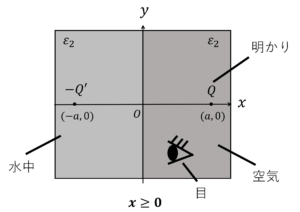
今度は，水の外から明かりを見ましょう。

すると，明かりの一部は水面で反射するので，明かりが2つあるように感じます。

ここで，$x=-a$の電荷$Q’$は，点電荷$Q$が作り出す電界の内,　境界面から跳ね返ってくる電界が作り出す電荷を表しています。

さて，実際に電界を求めていきましょう。

例題2

図のように，左半分に誘電率$\varepsilon_1$，右半分に誘電率$\varepsilon_2$の物質が満たされています。点電荷$Q$を$a，0$に配置したとき，

(1) $x \leq 0$における電界$E_1$を求めなさい。
(2) $x \geq 0$における電界$E_2$を求めなさい
(3) 境界条件を利用して，鏡像電荷$Q’，Q”$を$Q$を用いて表しなさい。
(4) (3)の結果を用いて，任意の点$(x，y)$における電界$E$を求めなさい。

例題2解答

(1)解答

$x \leq 0$のとき，鏡像法を用いると以下の図に書き換えられます。

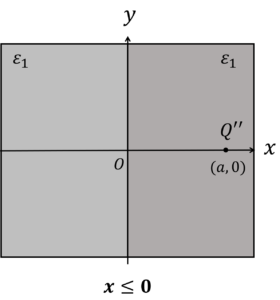
点電荷の周りに，半径$r$の球状ガウス面を取ると，ガウスの法則より

$\oint_{S}\underbrace{E_1}_{|E_1|i_r}･i_rdS=\frac{Q”}{\varepsilon_2}$

$|E_1|\underbrace{\oint_{S}dS}_{4\pi r^2}=\frac{ Q”}{\varepsilon_2}$

$|E_1|=\frac{ Q”}{4\pi \varepsilon_1 r^2}$

$E_1=\frac{ Q”}{4\pi \varepsilon_1 r^2}i_r$[V/m]

$E_1=\frac{ Q”}{4\pi \varepsilon_1 (\sqrt{(x-a)^2+y^2})^3}(x-a，y)\tag{1}$

となります。<終>

(2)解答

$x geq 0$のとき，鏡像法を用いると以下の図に書き換えられます。

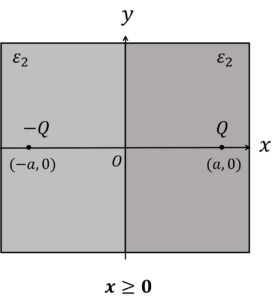
ここで，鏡像電荷$Q’$から点$(x，y)$の距離を$r’$とすると，求める電界$E_2$は，

$E_2=\frac{Q}{4\pi \varepsilon_2 r^2}i_r+\frac{Q’}{4\pi \varepsilon_1 r’^2}i_r’$

$E=\frac{1}{4\pi \varepsilon_2}[\frac{Q}{(\sqrt{(x-a)^2+y^2})^3}(x-a，y)+\frac{Q’}{(\sqrt{(x+a)^2+y^2})^3}(x+a，y)]\tag{2}$[V/m]

となります。<終>

(3)解答

$x=0$のとき，電界と電束密度の境界条件が成立している。

$E_1|_{x=0}×i_x=E_2|_{x=0}×i_x\tag{3}$

$D_1|_{x=0}･i_x=D_2|_{x=0}･i_x\tag{4}$

式(1)，式(2)を式(3)に代入すると，

$\frac{ Q”}{4\pi \varepsilon_1 (\sqrt{(-a)^2+y^2})^3}(-a，y)×i_x=\frac{1}{4\pi \varepsilon_2}[\frac{Q}{(\sqrt{(-a)^2+y^2})^3}(-a，y)+\frac{Q’}{(\sqrt{(a)^2+y^2})^3}(a，y)]×i_x$

$\frac{ Q”}{\cancel{4\pi} \varepsilon_1 \cancel{(\sqrt{a^2+y^2})^3}}\cancel{y}=\frac{1}{\cancel{4\pi} \varepsilon_2}[\frac{Q}{\cancel{(\sqrt{a^2+y^2})^3}}\cancel{y}+\frac{Q’}{\cancel{(\sqrt{(a)^2+y^2})^3}}\cancel{y}]$

$\frac{\varepsilon_2}{\varepsilon_1} Q”= Q-Q’\tag{5}$

式(1)，式(2)を式(4)に代入すると，

$\frac{ Q”}{\cancel{4 \pi}}(-a，y)･i_x= [\frac{Q}{\cancel{4\pi}}(-a，y)+\frac{Q‘}{\cancel{4\pi}}(a，y)]･i_x$

$ Q”= Q-Q‘\tag{6}$

式(5)と式(6)を連立させ，影像電荷$Q‘，Q”$を求めると，

$Q‘=\frac{2\varepsilon_1}{\varepsilon_1+\varepsilon_2}Q$

$Q”=\frac{\varepsilon_2-\varepsilon_1}{\varepsilon_1+\varepsilon_2}Q$

(4)解答

求める電界$E$は，

$x \leq 0$のとき，

$E=\frac{2\varepsilon_1}{\varepsilon_1+\varepsilon_2}Q \frac{1}{4\pi \varepsilon_1(\sqrt{(x-a)^2+y^2})^3}(x-a，y)$[V/m]

$x \geq 0$のとき，

$E=\frac{Q}{4\pi \varepsilon_2}[\frac{1}{(\sqrt{(x-a)^2+y^2})^3}(x-a，y)+\frac{\varepsilon_2-\varepsilon_1}{\varepsilon_1+\varepsilon_2} \frac{1}{(\sqrt{(x+a)^2+y^2})^3}(x+a，y)]$[V/m]

接地導体球の影像法

次に接地された半径$a$の導体球から距離$d$の位置に点電荷$Q$を配置したときの任意の点における電界$E$について考えましょう。

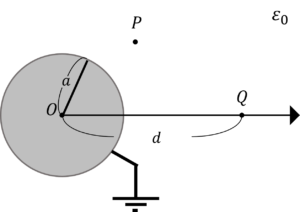
この場合，影像電荷を配置する位置に注意しましょう。鏡像法を適用すると，

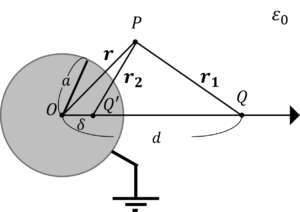
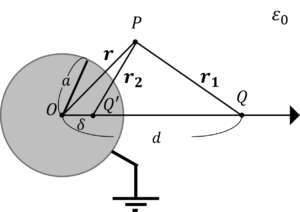
このようになります。

影像電荷$Q^{‘}$は導体表面の電位を0Vにするように原点から位置$\delta$だけずらします。

すると，影像電荷$Q^{‘}$と影像電荷の位置$\delta$は次式で表されます。

$Q^{‘}=-\frac{a}{d}Q$

$\delta=\frac{a^2}{d}$

例題3

影像電荷$Q’$と影像電荷の位置$\delta$が

$Q’=-\frac{a}{d}Q$

$\delta=\frac{a^2}{d}$

であることを示しなさい。

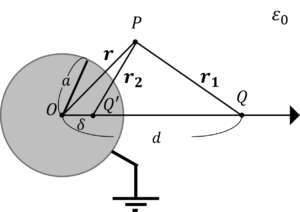
例題3解答

図を少し見やすくします。

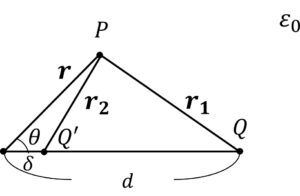
鏡像電荷$Q’$から任意の点までの距離$r_1$，点電荷$Q$から任意の点までの距離$r_2$とすると，電位$\phi$は，

$\phi=\frac{Q’}{4\pi \varepsilon_0 r_1}+\frac{Q}{4\pi \varepsilon_0 r_2}$[V]

となります。ここで，余弦定理から，$r_1$，$r_2$は，

$r_1=\sqrt{r^2+\delta^2-2r\delta \cos \theta}$
$r_2=\sqrt{r^2+d^2-2rd \cos \theta}$

となるので，電位$\phi$は，

$\phi=\frac{Q’}{4\pi \varepsilon_0 \sqrt{r^2+\delta^2-2r\delta \cos \theta}}+\frac{Q}{4\pi \varepsilon_0 \sqrt{r^2+d^2-2rd\cos \theta}}$

$r=a$において接地されているので，電位$\phi (a)=0$が成立します。

$\phi=\frac{Q’}{4\pi \varepsilon_0 \sqrt{a^2+\delta^2-2a\delta \cos \theta}}+\frac{Q}{4\pi \varepsilon_0 \sqrt{a^2+d^2-2ad \cos \theta}}=0$

$Q’=-\sqrt{\frac{ a^2+\delta^2-2a\delta \cos \theta }{ a^2+d^2-2ad \cos \theta }}Q$

$Q’=-\sqrt{\frac{\delta}{d}}\sqrt{\frac{\frac{a^2+\delta^2}{2a\delta}-\cos \theta}{\frac{a^2+d^2}{2ad}-\cos \theta}}Q$

ここで，影像電荷は$\theta$依らず一定でなければならないので，

$\frac{a^2+\delta^2}{2a\delta}=\frac{a^2+d^2}{2ad}$

が成立します。この式から$\delta$を求めます。

$d\delta^2-(a^2+d^2)\delta+da^2=0$

$(d\delta -a^2)(\delta-d)=0$

$\delta=\frac{a^2}{d}，\xcancel{d}$←$∵\delta < a$

$\delta$がもとまったので，影像電荷$Q’$も求まります。

$Q’=-\sqrt{\frac{a^2}{d}\frac{1}{d}}$

$Q’=-\frac{a}{d}$

<終>

大地から絶縁された導体球の鏡像法

接地した導体球鏡像法は鏡像法を用いて,次のように表されていました。

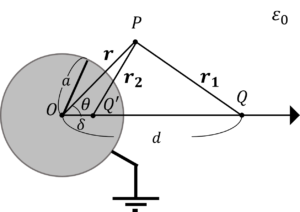
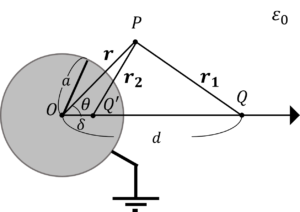
そこから更に,導体球を絶縁すると，原点に鏡像電荷$Q”$が出てきます。

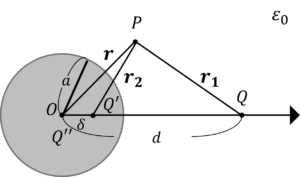
鏡像電荷$Q”$を求めましょう。

変化の前後で導体球は外部と絶縁されているので，電荷量保存則より，

$\underbrace{Q’+Q”}_{点電荷Qを置いた後の導体球の総電荷量}=\underbrace{0}_{点電荷Qを置く前の導体球の総電荷量}$

$Q”=-Q‘=\frac{a}{d}Q$

では，導体表面の電位$\phi (a)$はいくらになるでしょうか。

$\phi(a)=\frac{1}{4\pi \varepsilon_0}[\frac{Q”}{a}+\underbrace{\frac{Q’}{r_1}+\frac{Q}{r_2}}_{0}]$

$\phi=\frac{Q”}{4\pi \varepsilon_0 a}$

先ほど求めた$Q”$を代入すると，

$\phi=\frac{Q}{4\pi \varepsilon_0 r}$[V]

となります。

電気影像法：まとめ

今日のまとめ

2種類の誘電体の影像電荷$Q‘$，$Q”$
$$Q‘=\frac{\varepsilon_2-\varepsilon_1}{\varepsilon_1+\varepsilon_2}Q$$
$$Q”=\frac{2\varepsilon_1}{\varepsilon_1+\varepsilon_2}Q$$

接地導体球の影像電荷$Q”$，影像電荷の位置$\delta$，導体表面の電位$\phi$
$$Q”=-\frac{a}{d}$$
$$\delta=\frac{a^2}{d}$$
$$\phi=0$$

絶縁導体球の影像電荷$Q‘，Q”$，影像電荷$Q‘$の位置$\delta$，導体表面の電位$\phi$
$$\delta=\frac{a^2}{d}$$
$$Q‘=-\frac{a}{d}$$
$$Q”=\frac{a}{d}$$
$$\phi=\frac{Q}{4\pi \varepsilon_0 d}$$