$$\require{\cancel}$$
今日は,仮想変位とエネルギーについてのお話です。
静電エネルギー
1つの導体を\(Q\)に帯電させる為の仕事\(W\)
1つの導体に少しずつ電荷を与えて\(Q\)に帯電させましょう。
微小電荷\(dq\)を与える為に必要な仕事\(dW\)は,
\(dW=dq \phi \)
で表されます。
すると,1つの導体の電荷を\(Q\)にするための仕事は,次式のようになります。
\(W=\int_{0}^{Q}\underbrace{\phi}_{\frac{q}{C}} dq=\frac{Q^2}{2C}\)
※\(C\)は静電容量
\(Q=C\phi\)の関係式を使うと,\(W\)は,
\(W=\frac{Q^2}{2C}=\frac{1}{2}C\phi^2=\frac{1}{2}Q\phi \tag{1}\)
と書くことができます。この\(W\)は,静電界中に蓄えられるエネルギー(静電エネルギー)とも呼ばれます。
図1.電荷\(q\)に\(dq\)を徐々に加えて、\(Q\)[C]まで蓄える
導体が多数ある場合の仕事\(W\)
導体が多数ある場合,それぞれの導体を\(Q_1,Q_2,\cdots,Q_n\)まで帯電させ,導体の電位が\(\phi_1,\phi_2,\cdots,\phi_n\)になったとすると,仕事量\(W\)は,
\(W=\frac{1}{2}\sum_{i=1}^{n}Q_i\phi_i\tag{2}\)
となります。この式によれば,静電容量\(C_1,C_2,\cdots,C_n\)がわからなくても,電荷量と電位を計測するだけで仕事\(W\)をはかることができます。
真空中の単位体積当たりのエネルギー\(w_0\)
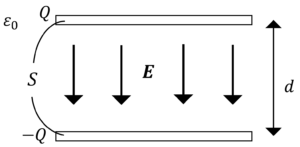
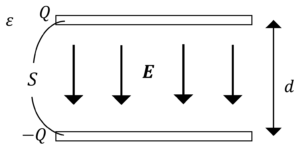
真空中コンデンサの単位体積当たりに蓄えられるエネルギー\(w_0\)について考えます。
コンデンサの\(C,\phi\)について,以下の関係式が成立していました。
\(C=\varepsilon_0 \frac{S}{d}\),\(\phi=Ed\)
よって,コンデンサの単位体積当たりに蓄えられるエネルギー\(w_0\)は,
\(w_0=\frac{W}{Sd}=\frac{1}{2Sd}C\phi^2\)
\(w_0=\frac{1}{2\cancel{Sd}}\varepsilon_0\frac{\cancel{S}}{\cancel{d}}E^2 \cancel{d^2}\)
\(w_0=\frac{1}{2}\varepsilon_0 |E|^2\)
誘電体中に蓄えられる単位体積あたりのエネルギー\(w\)
真空中に蓄えられる単位体積当たりのエネルギー\(w_0\)は,
\(w_0=\frac{1}{2}\varepsilon_0 |E|^2\)
でした。
誘電体中に蓄えられる単位体積当たりのエネルギー\(w\)は,誘電体の誘電率を\(\varepsilon\)とすれば,次のようにかけます。
\(w=\frac{1}{2}\varepsilon |E|^2=\frac{|D|^2}{2\varepsilon}=\frac{1}{2}E・D\tag{3}\)
しかし,式(3)は,\(\varepsilon\)が定数として扱えない強誘電体の場合には使えないので,一般化して,
\(w=\int_{0}^{D}E・dD\tag{4}\)
とする必要があります。
とはいえ,大学学部生ですら式(4)は扱わないので,覚えなくていいと思います。(こんなことを言ったらうちの教授に怒られそうな希ガス)
例題1
面積\(S\)の平行平板コンデンサに,誘電率\(\varepsilon_1,\varepsilon_2\),厚さ\(d_1,d_2\)の2枚の誘電体をもつコンデンサがあります。平板間に電位差\(V\)を加えるとき,
2つの誘電対中に蓄えられるエネルギーを等しくするには\(d_1,d_2\)をどのようにとれば良いだろうか。
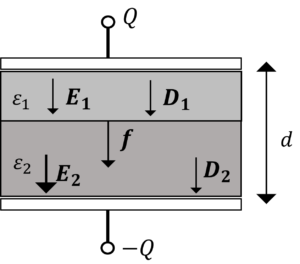
\(E_1,E_2\):誘電体内の電界
\(D_1,D_2\):誘電体内の電束密度
\(S\):極板の底面積
例題1解答
誘電率\(\varepsilon_1,\varepsilon_2\)に蓄えられるエネルギーをそれぞれ\(W_1,W_2\)すると,
\(W_1=\frac{1}{2}CV^2=\frac{1}{2}\varepsilon_1 \frac{S}{d_1}(E_1d_1)^2=\frac{|D|^2}{2\varepsilon_1}d_1S\)
\(W_2=\frac{|D|^2}{2\varepsilon_2}d_2S\)
\(W_1=W_2\)より,
\(\frac{d_1}{\varepsilon_1}=\frac{d_2}{\varepsilon_2}\)
となるように,\(d_1,d_2\)を設定すれば良いことがわかります。
<終>
仮想変位と力
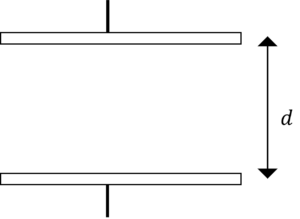
平行平板コンデンサの導体板に働く力を仮想変位の考え方を使って求めましょう。
仮想変位の考え方は,
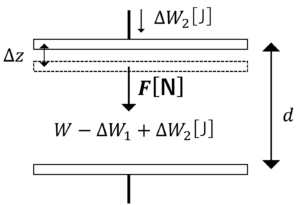
導体間に力が働き,上側の導体が\(\Delta z\)だけずれた(変位した)と考えます(実際には導体は動かない)。
そうすると,図中の\(F\)が導体に働く力であることがわかるので,
\(\underbrace{F\Delta z}_{した仕事}=-\underbrace{\Delta W_1}_{静電エネルギーの変化量}+\underbrace{\Delta W_2}_{電源からの供給エネルギー}\)
と表せます。
電荷が与えられたときの極板間に働く力\(F\)
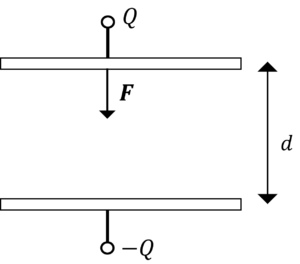
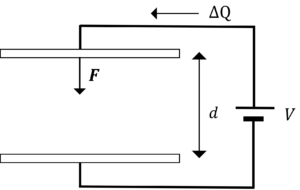
電荷\(Q\)が与えられた場合について考えます。
上側導体を\(\Delta z\)だけ下に移動させます。
変化後も,極板の電荷は減りません(電荷量保存の法則)。すると,力\(F\)は次のように表されます。
\(\underbrace{F\Delta z}_{電界がした仕事}=-\underbrace{\Delta W}_{静電エネルギーの減少量}+\underbrace{0}_{供給されるエネルギー}\)
よって,力\(F\)は,
\(F=-\frac{∂W}{∂z}|_{Q=const}\tag{5}\)
となります。\(const\)は,一定という意味があります。
つまり,\(Q=const\)は,\(\Delta z\)が変化しても,電荷\(Q\)は変化しないということです。
電位差が与えられたときの極板間に働く力\(F\)
次に極板間に電源が接続されている場合について考えましょう。
極板を下に\(\Delta z\)だけ動かします。
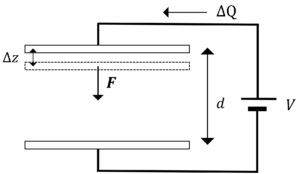
極板を動かしても,電位\(V\)は変わりません。すると,力\(F\)は次のように表されます。
\(\underbrace{F\Delta z}_{電界がした仕事}=-\underbrace{\Delta W}_{静電エネルギーの変化量}+\underbrace{V \Delta Q}_{電源から供給されるエネルギー}\)
\(F\Delta z=-\Delta W+2\Delta W=\Delta W\)
よって,求める力\(F\)は,
\(F=\frac{∂W}{∂z}|_{V=const}\tag{6}\)
となります。
例題2
図のように2種類の誘電体が平面で接しています。電界が境界面に垂直な場合,2つの誘電体の境界面に働く力\(f\)を求めましょう。

例題2解答
仮想変位させると、
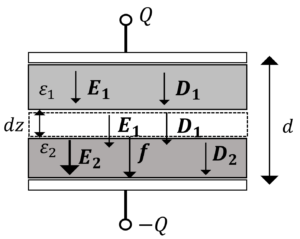

電荷\(Q\)は仮想変位前後で一定なので,
\(f=\frac{F}{\Delta S}=-\frac{\Delta W}{\Delta S \Delta z}|_{Q=const}=-\Delta w\)
ここで,\(\Delta w\)は,単位体積当たりのエネルギーの変化量を表しています。
\(\Delta w=\underbrace{\frac{1}{2}E_1・D_1}_{仮想変位によるエネルギー増加分}-\underbrace{\frac{1}{2}E_2・D_2}_{仮想変位によるエネルギー減少分}\)
単位面積当たりに働く力\(f\)は,
\(f=-w=\frac{1}{2}(E_2・D_2-E_1・D_1\)
電束密度に関する境界条件を用いると,\(D=D_1=D_2\)であるので,
\(f=\frac{|D|^2}{2}(\frac{1}{\varepsilon_2}-\frac{1}{\varepsilon_1})\)[N/m^2]
例題3
図のように2種類の誘電体が平面で接しています。電界が境界面に平行な場合,2つの誘電体の境界面に働く単位面積当たりに働く力\(f\)を求めましょう。

例題3解答
仮想変位させましょう。
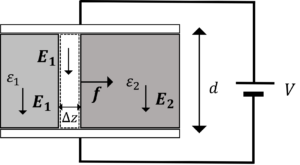

電位差\(V\)は,仮想変位前後で一定なので,
\(f=\frac{\Delta W}{\Delta S \Delta z}|_{V=const}=\Delta w\)
単位体積当たりのエネルギーの変化量\(\Delta w\)について,
\(w=\underbrace{\frac{1}{2}E_1・D_1}_{仮想変位によるエネルギー増加分}-\underbrace{\frac{1}{2}E_2・D_2}_{仮想変位によるエネルギー減少分}\)
ここで,電界に関する境界条件より,\(E=E_1=E_2\)が成立するので,
\(f=w=\frac{|E|^2}{2}(\varepsilon_1-\varepsilon_2)\)[N/m^2]
静電エネルギーと仮想変位:まとめ
1つの導体に蓄えられる静電エネルギー\(W\)
$$W=\frac{Q^2}{2C}=\frac{1}{2}C\phi^2=\frac{1}{2}Q\phi$$
\(n\)個の導体に蓄えられる静電エネルギー\(W\)
$$W=\frac{1}{2}\sum_{i=1}^{n}Q_i\phi_i$$
単位体積当たりのエネルギー\(w\)
$$w=\frac{|D|^2}{2\varepsilon}=\frac{1}{2}\varepsilon |E|^2=\frac{1}{2}E・D$$
$$F=-\frac{∂W}{∂z}|_{Q=const}$$
$$F=\frac{∂W}{∂z}_{V=const}$$
静電エネルギーと仮想変位:関連記事
電気学の総合演習問題

前回の電磁気学の記事


次回の電磁気学の記事


最後に
ある物体をずらしたときにエネルギーが減っていれば、その物体はずらした方向に力がかかっている。
エネルギーが増えていれば、その物体はずらした方向とは逆向きに力がかかっている。