$$\require{\cancel}$$
どうも,ユキです。
今日は,電流,電流密度ベクトルに関するお話です。
電流界
断面\(S\)を\(dt\)[s]間に\(dQ\)[C]の電荷が通過した時の電流\(i\)は次のように定義されます。
\(i=\frac{dQ}{dt}\tag{1}\)
しかし,電磁気学では電流\(i\)は計算に不向きな定義です。
理由は,細い導線に流れる電流を考える場合なら,電流の大きさだけを考えればいいですが,
広い断面を持つ導体を電流が流れる場合,場所によって,電流の向きや大きさが異なるからです。
そこで,電流密度\(j\)の出番です。任意の開曲面\(S\)を通る電流\(i\)は,
\(i=\int_{S}j・ndS\)
\(n\):単位ベクトル
とします。
直流,交流の違い
電流は定常電流,直流電流,交流電流の3つのタイプに分かれています。
| 定常電流: | 向きも大きさも変わらない電流 |
| 直流電流: | 大きさが変わっても向きが変わらない電流 |
| 交流電流: | 向きも大きさも変化する電流 |
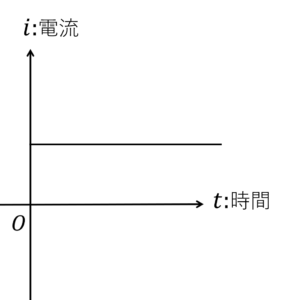
図1.定常電流
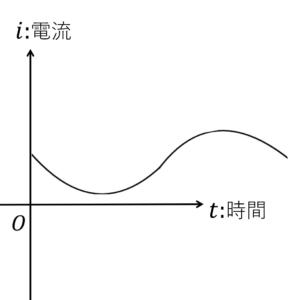
図2.直流電流
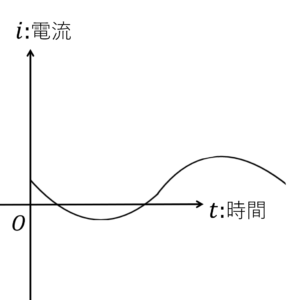
図3.交流電流
オームの法則
導線に電圧を加えると電流が流れます。このとき,電圧\(\phi\)[V]と電流\(i\)[i]の間には次のような比例関係が成立します。
\(\phi=Ri\tag{2}\)
式(2)の比例係数\(R\)を電気抵抗といい,単位はV/A=Ω(オーム)で表されます。
また,抵抗\(R\)の逆数はコンダクタンスと呼ばれ,
\(G=\frac{1}{R}\)
電流の流れやすさを示します。単位はS(ジーメンス)です。
抵抗
断面積\(S\),長さ\(l\)の棒状抵抗体
に関して,抵抗率を\(\rho \)とすると,抵抗\(R\)は,
\(R=\rho \frac{l}{S}\)
で表されます。
しかし,これでは,抵抗体の形が棒状である場合しか求められないので,
\(R=\rho \int_{0}^{l}\frac{1}{S}dl\tag{3}\)
とします。
こうすれば,場所によって断面積が異なる場合でも,抵抗の値を求めることができます。
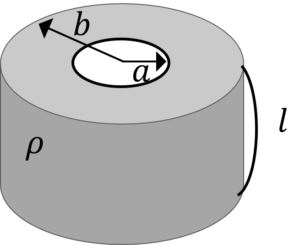
例題1
長さ\(l\),半径\(a\)の円筒電極と,これと同心の半径\(b\)の円筒電極の間の抵抗を求めなさい。ただし,電極間の物質の抵抗率は\(\rho\)とします。
例題1解答
式(3)を使います。
\(R=\rho \int_{a}^{b}\frac{dr}{2\pi r l}=\frac{\rho}{2\pi l}[\log r]_{a}^{b}=\frac{\rho}{2\pi l}\log \frac{b}{a}\)
となります。
ジュールの法則
導線中の2点A,Bを考えます。点Aの電位を\(\phi_A\),点Bの電位を\(\phi_B\)とすると,
電荷\(Q\)を点Bから点Aに運ぶのに必要な仕事量\(W\)[J:ジュール]は,
\(W=Q(\phi_A-\phi_B)\)
となります。更に,仕事率(電力)\(P\)[W:ワット]は\(\frac{dW}{dt}\)より
\(P=\frac{dW}{dt}=\underbrace{\frac{dQ}{dt}}_{i}\underbrace{(\phi_A-\phi_B)}_{\phi}=i\phi\tag{4}\)
式(4)に,オームの法則の関係である式(2)を代入すると,仕事率(電力)\(P\)は,
\(P=R i^2\tag{5}\)
式(5)の関係式を,ジュールの法則と呼びます。電力\(P\)は抵抗で熱に変換されて現れるので,ジュール熱と呼ばれます。
また,単位体積当たりのジュール熱を\(p\)[W/m^3]とすると,
\(p=\frac{\Delta P}{\Delta S \Delta l}=\frac{\Delta \phi \Delta i}{\Delta S \Delta l}\)
\(=\frac{E \cancel{\Delta l}・j \cancel{\Delta S}}{\cancel{\Delta S}\cancel{ \Delta l}}=j・E\)
よって,
\(p=j・E\tag{6}\)
となります。
キルヒホッフの法則
キルヒホッフの法則は,キルヒホッフ第1法則(電流則)とキルヒホッフ第2法則(電圧則)の2種類があります。
この法則は,電気回路学の基礎となっている法則です。
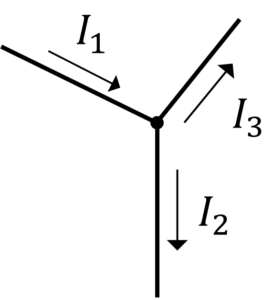
キルヒホッフ第1法則
定常的な電流を考えます。(\(\frac{dQ}{dt}=0\))
すると,\(i=\int_{S}j・ndS=0\)
となり,流れ出る電流と流れ出る電流は等しいことがわかります。
導線の接点に関してキルヒホッフ第1法則を適用すると,
\(-I_1+I_2+I_3=0\)
が成立します。この式をより一般的に書くと,
\(\sum_{i}I_i=0\tag{7}\)
キルヒホッフ第2法則
電界\(E\)は,静電界\(E_s\)と起電力\(\phi_e\)が発生させる電界\(E_e\)の和であるので,
\(E=E_s+E_e\)
ここで,両辺に閉曲線線積分を行うと,
\(\oint_{c}E・dr=\oint_{c}E_e・dr+\underbrace{\oint_{c}E_s・dr}_{0}=\oint_{c}E_e・dr\)
\(\oint_{c}E・dr=\oint_{c}\rho j・dr=I\oint_{c}\rho \frac{dr}{S}\)
\(\sum \phi_e=\sum RI\tag{8}\)
と書くことができます。
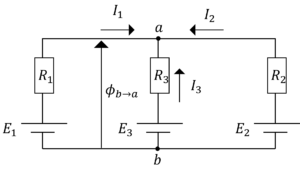
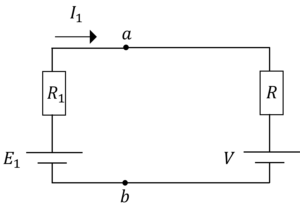
例題2
各回路に流れる電流\(I_1,I_2,I_3\)および,\(a,b\)間の電圧\(\phi_{ab}\)を求めなさい。
例題2解答
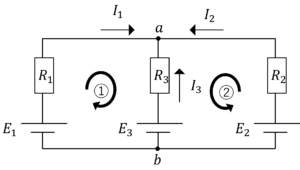
ループ①,ループ②を定義します。
ループ①,ループ②にキルヒホッフ第②法則を適用すると,
\(E_1-E_3=R_1I_1-R_3I_3\tag{9}\)
\(E_2-E_3=R_2I_2-R_3I_3\tag{10}\)
また,接点\(a\)にキルヒホッフ第1法則を適用すると,
\(I_1+I_2+I_3=0\tag{11}\)
式(9)~(11)を行列表示に書き直すと,
\(\left(\begin{array}{ccc}
E_1-E_3\\
E_2-E_3\\
0
\end{array}
\right)=\left(\begin{array}{ccc}
R_1&0&-R_3\\
0&R_2&-R_3\\
1&1&1
\end{array}
\right) \left(\begin{array}{ccc}
I_1\\
I_2\\
I_3\\
\end{array}
\right)\\ \)
クラメルの公式+サラス展開より,電流\(I_1,I_2,I_3\)は,それぞれ,
\(I_1=\frac{\left|\begin{array}{ccc}
E_1-E_3&0&-R_3\\
E_2-E_3&R_2&-R_3\\
0&1&1\end{array}\right|}{\left|\begin{array}{ccc}
R_1&0&-R_3\\
0&R_2&-R_3\\
1&1&1\end{array}\right|}=\frac{R_2(E_1-E_3)-R_3(E_2-\cancel{E_3})+R_3(E_1-\cancel{E_3})}{R_1R_2+R_2R_3+R_3R_1}\)
\(I_1=\frac{R_2(E_1-E_3)+R_3(E_1-E_2)}{R_1R_2+R_2R_3+R_3R_1}\)
\(I_2=\frac{\left|\begin{array}{ccc}
R_1&E_1-E_3&-R_3\\
0&E_2-E_3&-R_3\\
1&0&1
\end{array}\right|}{\left|\begin{array}{ccc}
R_1&0&-R_3\\
0&R_2&-R_3\\
1&1&1
\end{array}\right|}=\frac{R_1(E_2-E_3)-R_3(E_1-\cancel{E_3})+R_3(E_2-\cancel{E_3})}{R_1R_2+R_2R_3+R_3R_1}\)
\(I_2=\frac{R_1(E_2-E_3)+R_3(E_2-E_1)}{R_1R_2+R_2R_3+R_3R_1}\)
\(I_3=\frac{\left|\begin{array}{ccc}
R_1&0&E_1-E_3\\
0&R_2&E_2-E_3\\
1&1&0
\end{array}\right|}{\left|\begin{array}{ccc}
R_1&0&-R_3\\
0&R_2&-R_3\\
1&1&1
\end{array}\right|}=\frac{R_2(E_3-E_1)+R_1(E_3-E_2)}{R_1R_2+R_2R_3+R_3R_1}\)
※修正済み
よって,点\(a\),\(b\)の電位差\(\phi_{ab}\)は,
\(\phi_{ab}=E_3-R_3I_3=E_3-R_3\frac{R_2(E_2-E_1)+R_1(E_3-E_1)}{R_1R_2+R_2R_3+R_3R_1}\)
(別解)
テブナンの定理を利用します。
テブナンの定理を利用して,電流\(I_1\)を求めましょう。
まず,回路を\(a,b\)で切り離します。
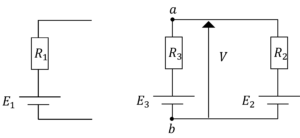
そして,\(a,b\)の電位差\(V\),\(a,b\)の合成抵抗\(R\)とすると,\(V,R\)はそれぞれ,
\(V=\frac{R_2}{R_2+R_3}E_3+\frac{R_3}{R_2+R_3}E_2\)
\(R=\frac{R_2R_3}{R_2+R_3}\)
となります。
テブナンの定理より,回路を書き換えると,
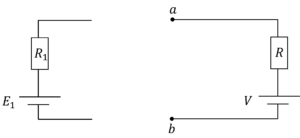
そして,再度回路をくっつけると,電源\(E_1\)と抵抗\(R_1\)には,\(I_1\)が流れるはずです。
よって,電流\(I_1\)は,
\(I_1=\frac{E_1-V}{R_1+R}=\frac{E_1-\frac{R_2}{R_2+R_3}E_3+\frac{R_3}{R_2+R_3}E_2}{R_1+\frac{R_2R_3}{R_2+R_3}}\)
\(I_1=\frac{R_2(E_1-E_3)+R_3(E_1-E_2))}{R_1R_2+R_1R_3+R_2R_3}\)
電流\(I_2,I_3\)も同様にすると求めることができます。
まとめ
電流\(i\)の定義
\(i=\frac{dQ}{dt}\)
キルヒホッフ第1法則:
接点に流れ込む電流と流れ出る電流は等しい
キルヒホッフ第2法則:
起電力の和=電流と抵抗の積
関連記事
前回の電磁気学の記事

次の電磁気学の記事
最後に
電磁気学から派生した学問に電気回路学という学問があります。電気回路を解く為の方法は,電気回路学で学んでください。