今日は電磁気学の静電誘導と静電と遮へい(シールド)についての記事です。
この記事を読むメリット
☑静電誘導と静電遮へいの問題を解くことができるようになる。
静電誘導とは
前回の記事で,導体の5つの性質について学びました。

静電誘導を説明するために,導体の性質1.と導体の性質2を使います。
導体の性質1.導体内部の電界は0
導体の性質2.電荷は導体表面のみに存在
導体に電荷を近づけた場合。
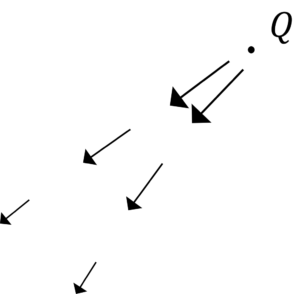
では早速,導体に\(Q\)[C]の電荷を近づけてみましょう。
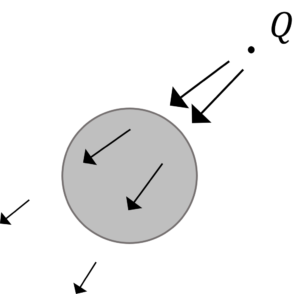
すると,
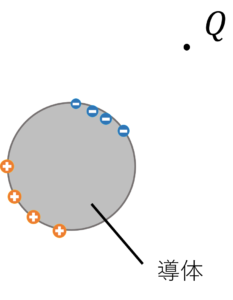
こうなります。
なぜ,電荷\(Q\)と逆向きの電荷が誘起されるのでしょうか?
その答えは一言で言えば,導体が,導体の性質1.を満たすように振る舞うからです。
この理屈は,導体表面に電荷が誘起されない場合を考えるとわかります。
まず,電荷\(Q\)を置きます。すると,当然のことながら電界が発生します。
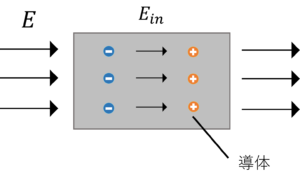
ここで,導体を置きましょう。
すると,この導体内には,電界が発生しているということになります。
しかし,このままでは,この導体は,導体の性質1.に反してしまいます。
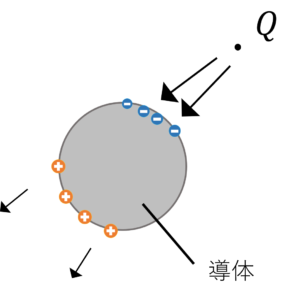
なので,導体内部の電界を0にする為に,
電荷側に負の電荷を,逆側には正の電荷を誘起させます(静電誘導)。
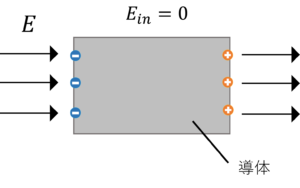
そうすることで,導体内部の電界は互いに打ち消し合い,
内部電界は0となります。
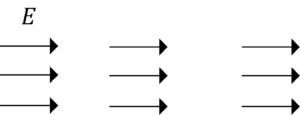
電界\(E\)を導体にかける
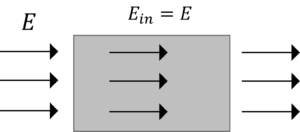
一様電界を考えます。
では,一様電界に導体を置いてみましょう。
ここで,導体は内部の電界を0とするために,電荷が誘起します。
電荷が導体表面に現れたとき,導体内部の電界は0になります。
例題1:
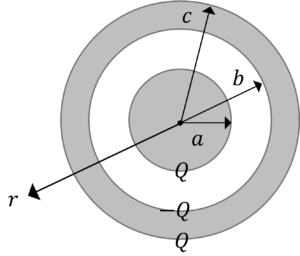
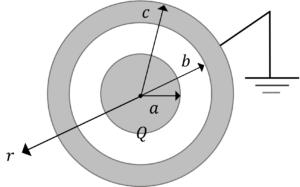
図のように,誘電率\(\varepsilon_0\)の空間に,半径\(a\)の内球と,内半径\(b\)で,外半径\(c\)の外球からなる同心球導体がある。いま,内球に\(Q\)を与えたとき,次の問に答えなさい。
(1) \(r\geq c\)のときの電界\(E_1\)と電位\(\phi_1\)
(2) \(b\leq r\geq c\)のときの電界\(E_2\)と電位\(\phi_2\)
(3) \(a\leq r\leq b\)のときの電界\(E_3\)と電位\(\phi_3\)
(4) \(r<a\)のときの電界\(E_4\)と電位\(\phi_4\)
例題1解答
(1) 解答
電荷は図のように誘起されます。
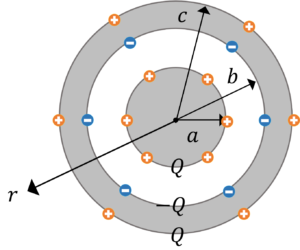
電界\(E_1\)について,
半径\(r\)のガウス面を考えると,ガウスの法則より,
\(\oint_{S} \underbrace{E_1}_{|E_1|i_r}・dS=\frac{Q-Q+Q}{\varepsilon_0}\)
\(|E_1|\underbrace{\oint_{S}dS}_{4\pi r^2}=\frac{Q}{\varepsilon_0}\)
\(|E_1|=\frac{Q}{4\pi \varepsilon_0 r^2}\)
よって,電界\(E_1\)は,
\(E_1=\frac{Q}{4\pi \varepsilon_0 r^2}i_r \)[V/m]
電位\(\phi_1\)について,
\(\phi_1=-\int_{\infty}^{r}\underbrace{E_1}_{|E_1|i_r}・i_r dr\)
\(\phi_1=-\int_{\infty}^{r}\frac{Q}{4\pi \varepsilon_0 r^2}dr\)
\(\phi_1=[\frac{Q}{4\pi \varepsilon_0 r}]_{\infty}^{r}\)
よって,電位\(\phi_1\)は,
\(\phi_1=\frac{Q}{4\pi \varepsilon_0 r}\)[V]
(2) 解答
電界\(E_2\)について,
導体内部の電界は0なので,
\(E_2=0\)[V/m]
また,電位\(\phi_2\)は,
\(\phi_2=-\int_{c}^{r}\underbrace{E_2}_{0}・i_rdr-\int_{\infty}^{c}E_1・i_rdr\)
\(\phi_2=\frac{Q}{4\pi \varepsilon_0 c}\)[V]
(3) 解答
電界\(E_3\)について,
半径\(r\)のガウス面を考えると,ガウスの法則より,
\(\oint_{S} \underbrace{E_3}_{|E_3|i_r}・dS=\frac{Q}{\varepsilon_0}\)
よって,電界\(E_3\)は,
\(E_3=\frac{Q}{4\pi \varepsilon_0 r^2} i_r \)[V/m]
また,電位\(\phi_3\)は,
\(\phi_3=-\int_{b}^{r}E_3・i_rdr -\int_{c}^{b}\underbrace{E_2}_{0}・i_rdr-\int_{\infty}^{c}E_1・i_rdr \)
\(\phi_3=-\int_{b}^{r}\frac{Q}{4\pi \varepsilon_0 r^2}dr+\frac{Q}{4\pi \varepsilon_0 c}\)
\(\phi_3=[\frac{Q}{4\pi \varepsilon_0 r}]_{b}^{r}dr+\frac{Q}{4\pi \varepsilon_0 c}\)
よって,電位\(\phi_3\)は,
\(\phi_3=\frac{Q}{4\pi \varepsilon_0}(\frac{1}{r}-\frac{1}{b}+\frac{1}{c})\)[V]
(4) 解答
電界\(E_4\)について,
半径\(r\)のガウス面を考えると,ガウスの法則より,
\(\oint_{S} \underbrace{E_1}_{|E_1|i_r}・dS=\frac{0}{\varepsilon_0}=0\)
よって,電界\(E_4\)は,
\(E_4=0\)[V/m]
電位\(\phi_4\)について,
\(\phi_3=-\int_{a}^{r}\underbrace{E_4}_{0}・i_rdr -\int_{c}^{b}\underbrace{E_2}_{0}・i_rdr -\int_{b}^{a}E_3・i_rdr -\int_{c}^{b}\underbrace{E_2}_{0}・i_rdr-\int_{\infty}^{c}E_1・i_rdr \)
よって,電位\(\phi_4\)は,
\(\phi_4=\frac{Q}{4\pi \varepsilon_0}(\frac{1}{a}-\frac{1}{b}+\frac{1}{c})\)[V]
静電遮へい(シールド)
静電遮へいとは,接地した導体で囲み,周りへの電界の影響をなくすことをいいます。
例えば,例題1で取り上げた同心球導体を考えましょう。
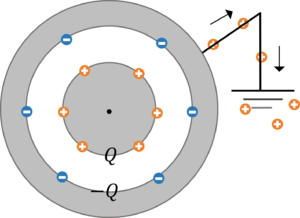
外球を接地すると,外側の電荷が地球へ逃げていきます。
こんな感じで静電遮へいをすることで,周りへ電界が出て行かなくなります。
本当に電界は出て行かないのでしょうか?
例題を使って確かめてみましょう。
例題2
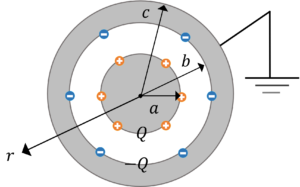
図のような同心導体球の内部導体に電荷\(Q\)を与えて,外部導体を接地したとき,次の問に答えなさい。
(1) \(r\geq c\)のときの電界\(E_1\)と電位\(\phi_1\)
(2) \(b\leq r\leq c\)のときの電界\(E_2\)と電位\(\phi_2\)
(3) \(a\leq r\leq b\)のときの電界\(E_3\)と電位\(\phi_3\)
(4) \(r<a\)のときの電界\(E_4\)と電位\(\phi_4\)
例題2解答
(1) 解答
電荷は図のように誘起されます。
電界\(E_1\)について,
半径\(r\)のガウス面を考えると,ガウスの法則より,
\(\oint_{S} \underbrace{E_1}_{|E_1|i_r}・dS=\frac{Q-Q}{\varepsilon_0}=0\)
よって,電界\(E_1\)は,
\(E_1=0\)[V/m]
電位\(\phi_1\)について,
\(\phi_1=-\int_{\infty}^{r}\underbrace{E_1}_{0}・i_r dr\)
よって,電位\(\phi_1\)は,
\(\phi_1=\frac{Q}{4\pi \varepsilon_0 r}\)[V]
(2) 解答
電界\(E_2\)について,
導体内部の電界は0なので,
\(E_2=0\)[V/m]
また,電位\(\phi_2\)は,
\(\phi_2=-\int_{c}^{r}\underbrace{E_2}_{0}・i_rdr-\int_{\infty}^{c}E_1・i_rdr\)
\(\phi_2=0\)[V]
(3) 解答
電界\(E_3\)について,
半径\(r\)のガウス面を考えると,ガウスの法則より,
\(\oint_{S} \underbrace{E_3}_{|E_3|i_r}・dS=\frac{Q}{\varepsilon_0}\)
よって,電界\(E_3\)は,
\(E_3=\frac{Q}{4\pi \varepsilon_0 r^2} i_r \)[V/m]
また,電位\(\phi_3\)は,
\(\phi_3=-\int_{b}^{r}E_3・i_rdr -\int_{c}^{b}\underbrace{E_2}_{0}・i_rdr-\int_{\infty}^{c}E_1・i_rdr \)
\(\phi_3=-\int_{b}^{r}\frac{Q}{4\pi \varepsilon_0 r^2}dr+0\)
\(\phi_3=[\frac{Q}{4\pi \varepsilon_0 r}]_{b}^{r}dr\)
よって,電位\(\phi_3\)は,
\(\phi_3=\frac{Q}{4\pi \varepsilon_0}(\frac{1}{r}-\frac{1}{b})\)[V]
(4) 解答
電界\(E_4\)について,
半径\(r\)のガウス面を考えると,ガウスの法則より,
\(\oint_{S} \underbrace{E_1}_{|E_1|i_r}・dS=\frac{0}{\varepsilon_0}=0\)
よって,電界\(E_4\)は,
\(E_4=0\)[V/m]
電位\(\phi_4\)について,
\(\phi_3=-\int_{a}^{r}\underbrace{E_4}_{0}・i_rdr -\int_{c}^{b}\underbrace{E_2}_{0}・i_rdr -\int_{b}^{a}E_3・i_rdr -\int_{c}^{b}\underbrace{E_2}_{0}・i_rdr-\int_{\infty}^{c}E_1・i_rdr \)
よって,電位\(\phi_4\)は,
\(\phi_4=\frac{Q}{4\pi \varepsilon_0}(\frac{1}{a}-\frac{1}{b})\)[V]
関連問題
前回の電磁気学

次の電磁気学

最後に
静電遮へいは別名シールドと呼ばれているそうです。確かに,電界から私たちを守るという意味でシールドと言えるかもしれませんね。