$$\require{cancel}$$
はじめに
対称性を持っている関数の代表例は,偶関数と奇関数です。
今回は,偶関数と奇関数を図や例題を踏まえつつ理解していただきたいと思います。
偶関数
\(f(-x)=f(x)\)
が成り立つ関数のことを言います。
偶関数の特徴
1.\(y\)軸で半分に折り曲げると重なる関数
2.2点\((-x,f(-x))\),\((x,f(x))\)の中点の座標は,\((0,f(x))\)
3.\(\int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx\)
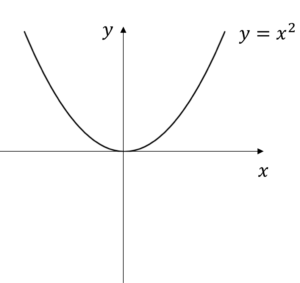
例えば,\(f(x)=x^2\)であれば,明らかに\(y\)軸で半分に折り曲げると重なる関数であることがわかります。
偶関数を\(y\)軸で折り曲げると,
重なります
2.2点\((-x,f(-x))\),\((x,f(x))\)の中点の座標は,\((0,f(x))\)
本当に中点が\((0,f(x))\)なのでしょうか?確認します。
2点\((-x,f(-x))\),\((x,f(x))\)中点の座標は,次のように表すことが出来ます。
\((\frac{-x+x}{2},\frac{f(-x)+f(x)}{2})\)
偶関数の定義から\(f(-x)=f(x)\)より,
\((\frac{-x+x}{2},\frac{f(x)+f(x)}{2})\)
よって,中点の座標は,\((0,f(x))\)
3番目の性質は,\(\int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx\)ですが,これは,\(y\)軸で折り曲げれば成立していることがわかりますが,一応証明します。
<証明>
\(\int_{-a}^{a}f(x)dx\)
\(=\int_{-a}^{0}f(x)dx+\int_{0}^{a}f(x)dx\)
第1項に着目して,\(x\)を\(-x\)に書き直すと,積分範囲が変わります。
\(=\int_{a}^{0}f(-x)d(-x)+\int_{0}^{a}f(x)dx\)
\(=\int_{0}^{a}f(-x)dx+\int_{0}^{a}f(x)dx\)
\(=\int_{0}^{a}f(x)dx+\int_{0}^{a}f(x)dx\) \((∵f(-x)=f(x))\)
よって,
\(=2\int_{0}^{a}f(x)dx\)
となるので,
\(\int_{-a}^{a}f(x)=2\int_{0}^{a}f(x)dx\)
<終>
奇関数
\(f(-x)=-f(x)\)
が成立する関数のことを言います。
奇関数の特徴
1.180°回転させると重なる関数
2.2点\(-x,f(-x)\),\(x,f(x)\)の中点は,\((0,0)\)
3.\(\int_{-a}^{a}f(x)dx=0\)
実際に,\(sin x\)を180°回転させましょう。
\(sin x\)を180°回転させると,
回転前と全く同じ形になります。
2.2点\((-x,f(-x))\),\((x,f(x))\)の中点の座標は,\((0,0)\)
これは,偶関数のときと同様に式変形をしていくとわかります。
3番目の性質は,\(\int_{-a}^{a}f(x)dx=0\)ですが,これは,図形の面積は回転させても値が変わらないということを知って入ればわかりますが,一応証明します。
\(\int_{-a}^{a}f(x)dx\)
\(=\int_{-a}^{0}f(x)dx+\int_{0}^{a}f(x)dx\)
\(=\int_{a}^{0}-f(-x)dx+\int_{0}^{a}f(x)dx\)
奇関数の性質から,\(f(-x)=-f(x)\)
\(=\int_{a}^{0}f(x)dx+\int_{0}^{a}f(x)dx\)
\(=\int_{0}^{a}-f(x)dx+\int_{0}^{a}f(x)dx\)
\(=0\)
となるので,
\(\int_{-a}^{a}f(x)dx=0\)

偶関数,奇関数を見分ける練習
では,ここで問題です。次の3つの関数は,偶関数でしょうか,それとも奇関数でしょうか
問題1:\(f(x)=x^2 sin x\)
問題2:\(f(x)=x^3 tan x\)
問題3:\(f(x)=\frac{e^{-x^2}}{cos x}\)
問題解答:
問題解答:奇関数,偶関数,偶関数
問題解説:
問題1の関数を見ていきます。
\(f(x)=x^2 sin x\)
ここで,\(x^2\)は偶関数で,\(sin x\)は奇関数なので,\(f(x)\)は偶関数×奇関数で奇関数です。実際に\(f(x)\)の\(x\)を\(-x\)に変えてみましょう。
\(f(-x)=(-x)^2sin (-x)=-x^2 sin x=-f(x)\)
つまり,
\(f(-x)=-f(x)\)
で奇関数であることが確かめられました。
問題2の関数は
\(f(x)=x^3 tan x\)
\(x^3\)は奇関数,\(tan x\)は奇関数なので,\(f(x)\)は奇関数×奇関数で偶関数になります。
実際に,
\(f(-x)=(-x)^3 tan -x=-x^3(-tan x)=x^3 tan x=f(x)\)
となり,偶関数です。
問題3の関数は,
\(f(x)=\frac{e^{-x^2}}{cos x}\)
ここで,\(e^{-x^2}\)は偶関数で,\(cos x\)も偶関数です。\(f(x)\)は偶関数×偶関数で,偶関数になります。
\(f(x)=\frac{e^{-(-x)^2}}{cos -x}=\frac{e^{-x^2}}{cos x}=f(x)\)
となって,偶関数になります。
この結果から次の3つのことが推測できます。
<div class=”simple-box3″><p>
1. 奇関数×奇関数=偶関数
2.偶関数×偶関数=偶関数
3.奇関数×偶関数=奇関数
</p></div>
では,証明します。
2つの関数\(f(x)\),\(g(x)\)の積を考えます。
\(f(x)\times g(x)\)
奇関数×奇関数=偶関数の証明
ゴール:\(h(-x)=h(x)\)
がいえれば,2つの奇関数の積は偶関数であるといえます。
<証明1>
\(f(x)\times g(x)\)
\(x\)を\(-x\)に変えます。
\(f(-x)\times g(-x)\)
ここで,2つの関数は共に奇関数なので,
\(-f(x)\times -g(x)=f(x)\times g(x)\) \(f(-x)=-f(x),g(-x)=-g(x)\)
ここで,\(f(x)g(x)=h(x)\)と置くと,
\(h(-x)=h(x)\)
となって,2つの奇関数の積は偶関数であることが確かめられました。
奇関数×偶関数=奇関数の証明
ゴール:\(h(-x)=h(x)\)
がいえれば,2つの奇関数の積は偶関数であるといえます。
<終>
<証明2>
\(f(x)\times g(x)\)
\(x\)を\(-x\)に変えます。
\(f(-x)\times g(-x)\)
ここで,2つの関数は共に偶関数なので,
\(f(-x)\times g(-x)=f(x)\times g(x)\) \(f(-x)=f(x),g(-x)=g(x)\)
ここで,\(f(x)g(x)=h(x)\)と置くと,
\(h(-x)=h(x)\)
となって,2つの奇関数の積は偶関数であることが確かめられました。
<終>
<証明3>
\(f(x)\times g(x)\)
\(x\)を\(-x\)に変えます。
\(f(-x)\times g(-x)\)
ここで,\(f(x)\)を奇関数,\(g(x)\)を偶関数とすると,
\(f(-x)\times g(-x)=-f(x)\times g(x)\) \(f(-x)=-f(x),g(-x)=g(x)\)
ここで,\(f(x)g(x)=h(x)\)と置くと,
\(h(-x)=-h(x)\)
となって,2つの奇関数の積は偶関数であることが確かめられました。
<終>
難問:\(log x^2\)は偶関数かそれとも奇関数なのか?
この問題の解答として2パターンが考えられます。
パターン1:
\(f(-x)=log (-x)^2=log x^2=f(x)\)
より偶関数
これは普通の解き方ですが,中にはパターン2のような考え方をした人もいるのではないでしょうか。
パターン2:
\(f(-x)=log (-x)^2=2 log -x\)
\(-x>0\)から,\(x<0\)となるので,関数\(f(x)\)は,偶関数でも奇関数でもない。
パターン2は,対数の性質を使って,真数の指数部分をlogの前に持ってきています。考え方は面白いですが,式変形が間違っています。これは,実際に値を代入してみればわかります。例えば,変形前の式である\(log x^2\)の\(x\)に2つの数+1,-1を代入してみましょう。
\(log 1^2=0\)
\(log (-1)^2=0\)
次に,変形後の式\(2log (-x)\)に2つの数+1,-1を代入してみます。
\(2log (-1)\) \(\cdots\)不適
\(log -(-1)=0\)
+1を代入できません。式変形前と式変形後の結果が変わるはずはないのでどこかが間違っているということになります。
答えは,ここです。
\(log (-x)^2=\xcancel{2 log -x}\)
正しくはこのように書きます。
\(log (-x)^2=log |x|^2=2log |x|\)
このように式変形をすると,
\(f(-x)=2log |-x|=2log |x|\)
という結果が得られて\(f(x)\)は偶関数ということがわかりました。

まとめ
1.偶関数は\(y\)軸対称
2.奇関数は\(y=-x\)で対称。
3.偶関数×偶関数=偶関数
4.奇関数×奇関数=奇関数
5.偶関数×奇関数=奇関数
6.\(log x^2\)は偶関数
最後に
偶関数と奇関数の性質を使うと積分が簡単に解けることがあります。
偶関数と奇関数を意識しつつ問題を解きましょう。\(log x^2\)のような対数関数で,真数の指数を前に持ってくる際には,絶対値に気をつけて式変形を行ってください。