電磁気学Ⅳ演習問題(後半部)

ユキ

電磁気学Ⅳのテスト勉強用です。

この記事を読むメリット
☑電磁気学Ⅳのテスト勉強

問題3

問題3：
図のような磁路長$l$m，断面積$S$[m^2]，比透磁率$μ_r$の磁性体を用いて$N$巻のリング状コイルを作成し電流を流したところ，磁性体は周方向に磁化され，磁化の大きさは$M$[A/m]であった。漏れ磁束はないものとするとき，流した電流を求めよ。

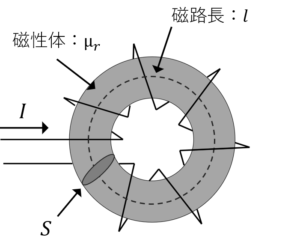
問題3解答

磁化の大きさ$|M|$と磁束の大きさ$|H|$の関係式は，

$|M|=\frac{B}{μ_0}-H=(μ_r-1)|H|\tag{1}$

続いて，磁束$|H|$と電流$I$の関係式は，アンペールの周回積分の法則より，

$\oint_C H･ds=NI$

$|H|\underbrace{\oint_C ds}_{磁路長：l}=NI$

$|H|=\frac{NI}{l}\tag{2}$

式(1)，式(2)から，磁化の大きさ$|M|$と電流$I$の関係式は，

$|M|=(μ_r-1)\underbrace{\frac{NI}{l}}_{H}$

$I=\frac{|M|l}{N(μ_r-1)}$[A]

<終>

自動制御に関する記事ー＞

自動制御Ⅰ演習問題(2018年度)ベクトル線図、ブロック線図、ナイキスト線図、ラウスの安定判別法、ブロック線図から伝達関数を求める問題。ラプラス変換、逆ラプラス変換を使って解く問題などがあります。...

問題4

問題4：
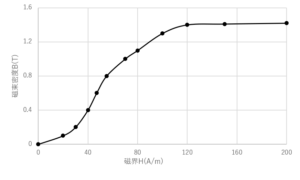
図のような磁化特性を持つ磁性体を用いて，ギャップを設けたリング状コイルを作成した。磁性体の磁路長は100mm，断面積は50mm^2であり，ギャップ長は10mm，巻数は500巻きである。このコイルの動作磁束密度を0.4Tにしたいとき，何Aの電流を流せば良いか？漏れ磁束はないものとする。

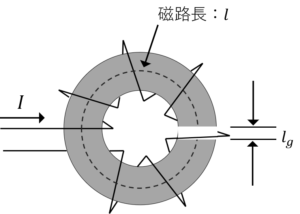
問題4解答

等価磁気回路を下に示す。

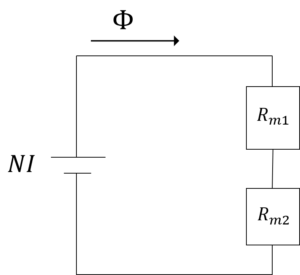
このとき，電流$I$は，

$I=\frac{1}{N}\underbrace{Φ}_{BS}(\underbrace{R_{m1}}_{\frac{l}{μ_0μ_r S}}+\underbrace{R_{m2}}_{\frac{l_g}{μ_0 S}})$

$I=\frac{B}{N}(\frac{l}{μ_0μ_r}+\frac{l_g}{μ_0})\tag{1}$

ここで，グラフより$μ_0μ_r$を求めると，

$μ_0μ_r=\frac{B}{H}=\frac{0.4}{40}=0.01\tag{2}$

よって，式(1)，式(2)より電流$I$は，

$I=\frac{0.4}{500}(\frac{100\times 10^{-3}}{0.01}+\frac{10\times 10^{-3}}{4\pi \times 10^{-7}})=6.37$A

問題5

問題5：
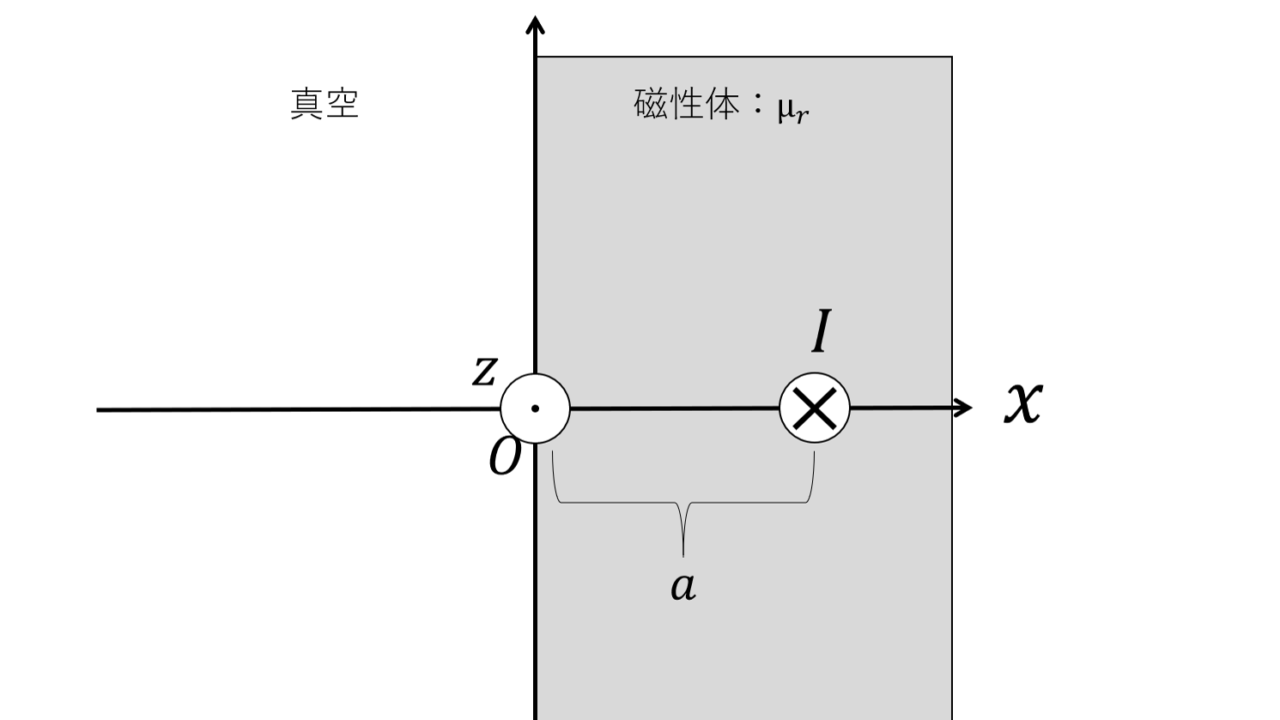
図のように$x=0$の平面で真空部と接する半無限長の磁性体(比透磁率は$μ_r$)がある。$x=a$の位置に配置した無限長導体の$-z$方向に電流$I$を流したときに，各部の磁界を求めるのに必要な(=境界条件を満足する)鏡像電流の位置並びに大きさを求めよ。

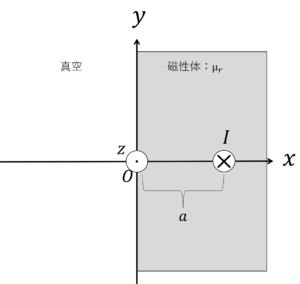
問題5解答

真空と磁性体の境界である点$(0,y)$の磁界と磁束密度について考える。

真空の磁界と磁束密度をそれぞれ$H_0$，$B_0$，磁性体の磁界と磁束密度をそれぞれ$H_{mag}$，$B_{mag}$とすると，

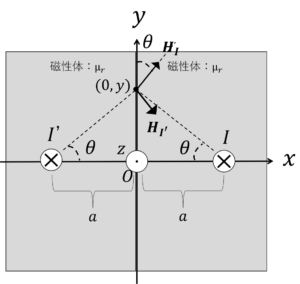
$H_{mag}=\underbrace{\frac{I}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+\frac{I}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y}_{Iが作る磁界}+$

$\underbrace{\frac{I’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x-\frac{I’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y}_{I’が作る磁界} $

$H_{mag}=\frac{I+I’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+\frac{I-I’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y \tag{1}$

$B_{mag}=μ_0μ_r\frac{I+I’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+μ_0μ_r\frac{I-I’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y \tag{2}$

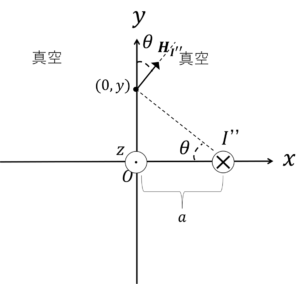
$H_{0}=\underbrace{\frac{I’’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+\frac{I’’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y}_{I’’が作る磁界}\tag{3}$

$B_{0}=μ_0\underbrace{\frac{I’’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+μ_0\frac{I’’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y}_{I’’が作る磁界}\tag{4}$

ここで，$x=0$における磁界と磁束密度の境界条件は，

$H_{0}\times i_x=H_{mag}\times i_x\tag{5}$

$B_{0}･i_x=B_{mag}･i_x\tag{6}$

式(5)に，式(1)と式(3)を代入。
$(\frac{I’’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+\frac{I’’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y)\times i_x=$

$\frac{I+I’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+\frac{I-I’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y )\times i_x$

$I’’=I-I’\tag{7}$

式(6)に，式(2)と式(4)を代入。

$(μ_0\frac{I’’}{2\pi \sqrt{a^2+y^2}}\sin \theta i_x+μ_0\frac{I’’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y)･i_x$

$=(μ_0μ_r\frac{I+I’}{2\pi \sqrt{a^2+y^2}}\sin \theta　i_x+μ_0μ_r\frac{I-I’}{2\pi \sqrt{a^2+y^2}}\cos \theta i_y)･i_x$

$I’’=μ_r(I+I’)\tag{8}$

式(7)と式(8)の連立方程式を解くと

$I’’=\frac{2μ_r}{1+μ_r}I$

$I’=\frac{1-μ_r}{1+μ_r}I$

<終>

問題6

問題6：
図のような三脚磁気回路がある。磁性体の比透磁率$μ_r$は1,000，中央部の断面積$S_0$は200cm^2，その他の部分の断面積$S_1$は100cm^2，$l_1=40.0$cm，$l_2=160cm$，$N_1=1,000$，$N_2=2,000$，$I_1=5.00$A，$I_2=10.0$A，ギャップ長$d=2.00$cmである。ギャップ部の磁束密度$B_0$を有効数字3桁で求めよ。上から下方向へ磁束が流れる場合を正とせよ。

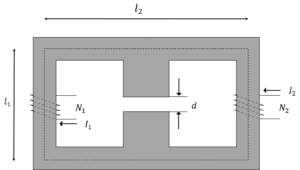
問題6解答

等価磁気回路を以下に示す。

<準備>
磁気抵抗をそれぞれ，$R_{m1}$，$R_{m2}$，$R_{m3}$
$R_{m1}=R_{m3}=\frac{l_1+l_2}{μ_0μ_r S_1}=\frac{5l_1}{μ_0μ_r S_1}$
$R_{m2}=\frac{l_1-d}{μ_0μ_r S_0}+\frac{d}{μ_0 S_0}=\frac{l_1-d}{μ_0μ_r 2S_1}+\frac{d}{μ_02 S_1}$

$N_2I_2=20 \times 10^3$

$N_1I_1=5 \times 10^3$

<準備終了>

ここで，テブナンの定理を用いて計算する。

1-1’間の起磁力$V_0$は，

$V_0=N_2I_2\frac{R_{m3}}{R_{m1}+R_{m3}}-N_1I_1\frac{R_{m1}}{R_{m1}+R_{m3}}$

$V_0=\frac{1}{2}(N_2I_2-N_1I_1)$

1-1’から見た合成磁気抵抗$R_{m0}$は，

$R_{m0}=\frac{R_{m1}R_{m3}}{R_{m1}+R_{m3}}$

$R_{m0}=\frac{R_{m1}}{2}$

テブナンの定理より，磁束$Φ$は，

$Φ=\frac{V_0}{R_{m2}+R_{m0}}$

$Φ=\frac{\frac{1}{2}(N_2I_2-N_1I_1)}{\underbrace{\frac{l_1-d}{μ_0μ_r2S_1}+\frac{d}{μ_02 S_1}}_{R_{m2}}+\frac{R_{m1}}{2}}$

磁束密度$B_0$について，

$\underbrace{B_{0}}_{\frac{Φ}{S_0}=\frac{Φ}{2S_1}}=\frac{1}{2S_1}\frac{\frac{1}{2}(N_2I_2-N_1I_1)}{ \frac{l_1-d}{μ_0μ_r 2S_1}+\frac{d}{μ_02 S_1} +\frac{5 l_1}{2μ_0μ_r S_1}}$

$B_0=\frac{\frac{μ_0μ_r }{2}(N_2I_2-N_1I_1)}{ l_1-d+μ_rd +5 l_1}$

$B=\frac{\frac{1000 \times 4\pi \times 10^{-7}}{2}(20-5)\times 10^3}{22.38}$

$B=\frac{3\pi}{22.38}=0.421$[T]

<終>

電気学の演習問題ー＞

[電磁気学Ⅱ]演習問題電磁気学の内の電気学の部分の集大成もかねて,演習問題としました。ただし,この問題の答えはあっているとは限らないので,引用の際は,ご注意願います。...

問題7

問題7：
十分広い面を持つ比透磁率$μ_r$の2つの磁性体を距離$l$隔てて真空中に平行に配置し，磁性体から角度$\theta$で磁束密度$B$(=$|B|$)を真空領域に入射した。この2つの磁性体間に働く単位面積あたりの力の大きさを求めよ。

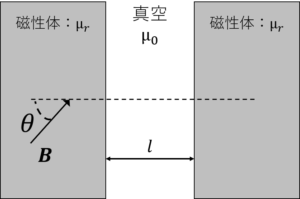
問題7解答

磁性体を右方向に$Δz$だけ仮想変位させたとき，真空中にたくわえる磁気エネルギーの変化量を$ΔW$とすると，単位面積あたりに働く力の大きさ$|f|$は

$f=-\frac{ΔW}{Δz}$

となる。

ここで，真空の磁界と磁束密度を$H_0$，$B_{0}$，磁性体内の磁界と磁束密度を$H_{mag}$，$B_{mag}$とすると，

$B_{0}=|B|\cos \theta i_x+|B|\sin \theta i_y\tag{1}$

$H_{0}=\frac{|B|}{μ_0}\cos \theta i_x+\frac{|B|}{μ_0}\sin \theta i_y \tag{2}$

$B_{mag}=| B_{mag}|\cos \theta ‘ i_x+| B_{mag}|\sin \theta ‘ i_y \tag{3}$

$H_{mag}=\frac{|B_{mag}|}{μ_0μ_r}\cos \theta ‘ i_x+\frac{|B_{mag}|}{μ_0μ_r}\sin \theta ‘ i_y \tag{4}$

ここで，磁界と磁束密度の境界条件を用いると，

$H_{0}\times i_x=H_{mag}\times i_x$

$B_{0}･i_x=B_{mag}･i_x$

式(5)に式(2)，式(4)を代入すると，

$(\frac{|B|}{μ_0}\cos \theta i_x+\frac{|B|}{μ_0}\sin \theta i_y)\times i_x=(\frac{|B_{mag}|}{μ_0μ_r}\cos \theta ‘ i_x+\frac{|B_{mag}|}{μ_0μ_r}\sin \theta ‘ i_y)\times i_x$

$\frac{|B|}{μ_0}\sin \theta =\frac{|B_{mag}|}{μ_r}\sin \theta ‘\tag{7}$

$(|B|\cos \theta i_x+|B|\sin \theta i_y)･i_x=(| B_{mag}|\cos \theta ‘ i_x+| B_{mag}|\sin \theta ‘ i_y)･i_x$

$|B|\cos \theta =| B_{mag}|\cos \theta ‘\tag{8}$

式(7)，式(8)を式(1)，式(2)に代入すると，

$B_0=|B|\cos \theta i_x+\frac{|B|}{μ_r}\sin \theta i_y $

$H_0=\frac{|B|}{μ_0}\cos \theta i_x+\frac{|B|}{μ_0μ_r}\sin \theta i_y $

単位体積当たりの磁気エネルギー$w$は，

$w=\frac{1}{2}B_0･H_0=\frac{|B_0|^2}{2μ_0}$

$w=\frac{|B|^2}{2μ_0}\cos^2 \theta+\frac{1}{2μ_r^2}\sin^2 \theta$

ここで，真空中にたくわえる磁気エネルギーの変化量$ΔW$は，

$ΔW=w(l-Δz)-wl=-wΔz$

よって，$|f|$は，