電磁気学Ⅳ演習(前半部)

ユキ

電磁気学の演習問題の解答例です。

あっている保証はないので，引用する場合は自己責任でお願いします。

この記事を読むメリット

☑電磁気学Ⅳのテスト対策

演習(前半部)

問題3

問題3：
磁気分極$J$が以下の形で与えられているとき，磁極密度(磁荷密度)$\rho_m$を求めよ。
(1) $(log_{10} x+y)i_x-2e^{-xz}i_y+2^{z}i_z$
(2) $\frac{\sin \theta}{r}i_r+\tan \phi i_{\phi}+ln (r\phi)i_{\theta}$

問題3解答

$\rho_m=∇･J$を使います。

(1) 解答

$\rho_m=\frac{\partial}{\partial x}(log_{10} x+y)i_x･i_x+\frac{\partial}{\partial y}(-2e^{-xz})i_y･i_y+\frac{\partial}{\partial z}2^{z}i_z･i_z$

$\rho_m=\frac{1}{x ln 10}+2^{z}ln 2$[T/m]

<終>

(2) 解答

$\rho_m=\frac{1}{r^2}\frac{\partial}{\partial r}(r^2･\frac{\sin \theta}{r})i_r･i_r+\frac{1}{r\sin \theta}\frac{\partial}{\partial \phi}+\tan \phi i_{\phi}･i_{\phi}･i_{\phi}+\frac{1}{r\sin \theta}\frac{\partial}{\partial \theta}\sin \theta ln(r\phi)i_{\theta}･i_{\theta}$

$\rho_m=\frac{\sin \theta}{r^2}+\frac{1}{r\sin \theta \cos^2 \phi}+\frac{1}{r\sin \theta}\cos \theta ln(r\phi)$

よって，求める$\rho_m$は，

$\rho_m=\frac{\sin \theta}{r^2}+\frac{1}{r\sin \theta \cos^2 \phi}+\frac{1}{r\tan \theta}ln(r\phi)$[T/m]

<終>

自動制御の演習問題に関する記事ー＞

自動制御Ⅰ演習問題(2017年度)2017年度自動制御Ⅰの演習問題です。ラウス･フルビッツの安定判別法,ブロック線図，ボード線図，ナイキスト線図を描く問題を取りそろえました。大学の試験勉強用にお使いください。...

問題4

問題4：
磁性体を鉄心に用いた環状コイルに電流を流したところ，鉄心中の磁界の大きさが400A/m，磁束密度の大きさが0.404Tであった。この磁性体の比透磁率$μ_r$及び磁化の大きさ$|M|$を有効数字3桁で求めよ。

問題4解答

磁化の大きさ$|M|$について，

$|M|=\frac{|B|}{μ_0}-|H|=\frac{0.404}{4.0\pi \times 10^{-7}}-400≒3.21\times 10^5$[A/m]

比透磁率について，$B=μ_0μ_r |H|$より，

$μ_r=\frac{|B|}{μ_0|H|}=\frac{0.404}{4.0\pi\times 10^{-7}\times 400}≒804$

問題5

問題5：
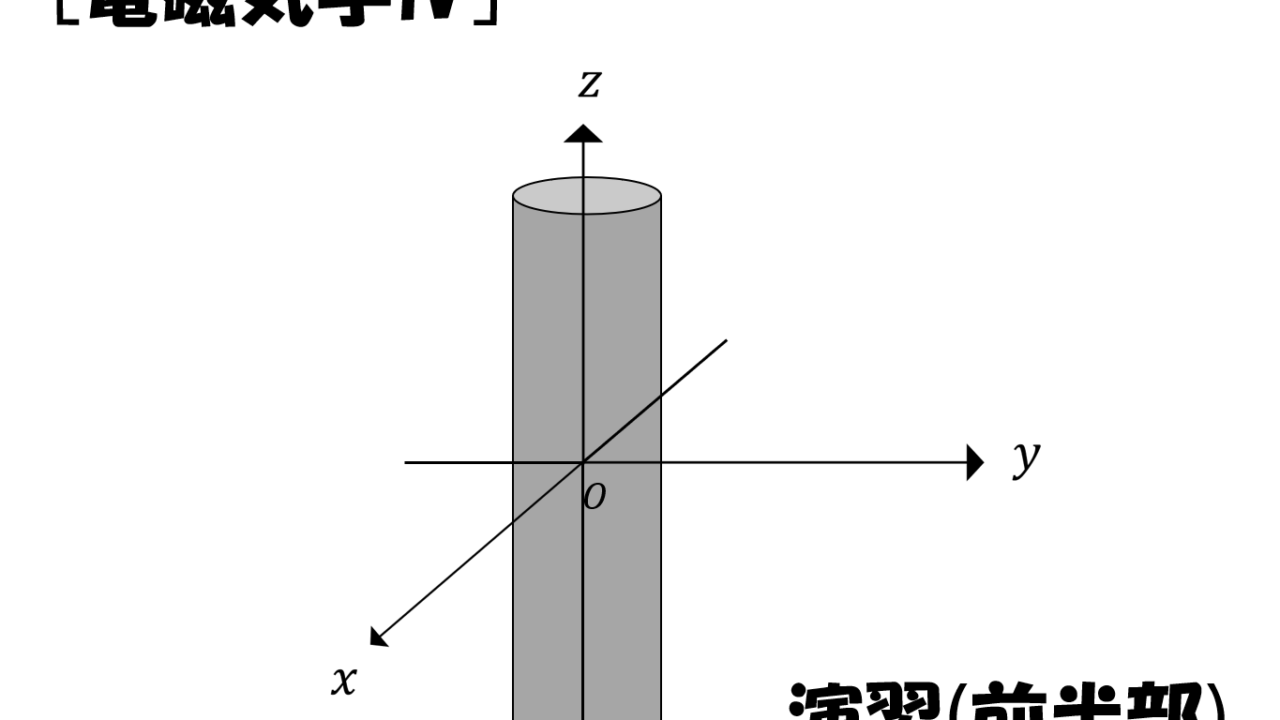
$z$方向に無限に長い円柱状の磁性体の$z$方向に$H_0=100i_z$[kA/m]の一様磁界を加えたところ，磁性体は印加磁界方向に一様に磁化し，そのときの磁気分極値は0.1Tであった。以下の問に有効数字3けたで解答せよ。
(1) このときの磁性体内部の磁界$H_{in}$を求めよ。
(2) 印加磁界方向を$z$方向から$x$方向に変化させたとき，磁気分極値が0.05Tであった。このときの磁性体内部の磁界$H_{in}$はいくらになるか？

問題5解答

(1) 解答

$H_{in}=H_0+H_d$

$z$方向に無限に長い磁性体なので，反磁界係数$N_z=0$，従って，$H_d$は

$H_d=-N_zM=0$[A/m]

よって，

$H_{in}=H_0=10^5i_z$[A/m]

(2) 解答

$H_{in}=H_0+H_d$

$H_0$は，

$H_0=10^5i_x$

$H_d$について，反磁界係数$N_x=\frac{1}{2}$より

$H_d=-\frac{1}{2}M=-\frac{J}{2µ_0}=\frac{0.05}{2・4\pi \times 10^{-7}}i_x$

よって，$H_{in}$は，

$H_{in}=10^5i_x-\frac{0.05}{2・4\pi \times 10^{-7}i_x}=8.01\times 10^4$[A/m]

問題6

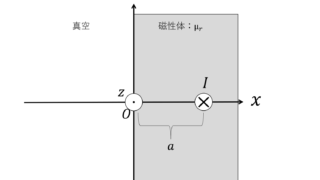
真空中に十分広い面を持つ比透磁率が$µ_{r1}$の磁性体Ⅰと$µ_{r2}$の磁性体Ⅱを図のように真空中に配置し，磁性体Ⅰに角度$\theta_0$で磁束密度$B_0$を入射した。
(1) 磁性体Ⅱ内での磁界$H_2$および磁束密度$B_2$を$B_0，µ_0，µ_1，µ_2，\theta_0$を用いて表せ。
(2) 磁性体Ⅰ内部の時期エネルギー$w_{m1}$を求めよ。

問題6解答

(1) 解答

真空の磁束密度$B_0$について，

$B_0=|B_0|\cos \theta_0 i_x+|B_0|\sin \theta_0 i_y\tag{1}$

磁性体Ⅱの磁束密度$B_{mag}$について，

$B_{2}=|B_{2}|\cos \theta i_x+|B_{2}|\sin \theta i_y\tag{2}$

真空の磁界$H_{0}$について，

$H_0=|H_0|\cos \theta_0 i_x+|H_0|\sin \theta_0 i_y$

$H_0=\frac{|B_0|}{µ_0}\cos \theta_0 i_x+\frac{|B_0|}{µ_0}\sin \theta_0 i_y\tag{3}$

磁性体Ⅱの磁界$H_{2}$について，

$H_{2}=|H_{2}|\cos \theta i_x+|H_{2}|\sin \theta i_y$

$H_{2}=\frac{|B_{2}|}{µ_0 µ_{r2}}\cos \theta i_x+|\frac{B_{2}|}{µ_0 µ_{r2}}\sin \theta i_y\tag{4}$

ここで，磁界と磁束密度の境界条件
$H_{0}\times i_x=H_{2} \times i_x$
$B_{0}・i_x=B_{2}・i_x$

の2式で式(1)~(4)を吟味すると，

$\frac{|B_0|}{µ_0} \sin \theta_0=|B_{2}||µ_0µ_{r2}|\sin \theta\tag{5}$

$|B_0| \cos \theta_0=|B_{2}|\cos \theta\tag{6}$

よって，式(5)，式(6)より磁界$H_2$，磁束密度$B_2$は，

$H_{2}=\frac{|B_{0}|}{µ_0 µ_{r2}}\cos \theta_0 i_x+|\frac{|B_{0}|}{µ_0}\sin \theta_0 i_y$

$B_{2}=|B_{0}|\cos \theta_0 i_x+µ_{r2}|B_{0}|\sin \theta_0 i_y$

<終>

(2) 解答

$w_{m1}=\frac{1}{2}B_{1}・H_{1}$

$w_{m1}=\frac{1}{2}(\frac{|B_{0}|}{µ_0 µ_{r1}}\cos \theta_0 i_x+|\frac{|B_{0}|}{µ_0}\sin \theta_0 i_y)・(|B_{0}|\cos \theta_0 i_x+µ_{r1}|B_{0}|\sin \theta_0 i_y)$

$w_{m1}=\frac{1}{2}(\frac{|B_{0}|^2}{µ_0 µ_{r1}}\cos^2 \theta_0 +\frac{µ_{r1}|B_{0}|^2 }{µ_0}\sin^2 \theta_0)$

$w_{m1}=\frac{|B_0|^2}{2}(\frac{\cos^2 \theta_0}{µ_0 µ_{r1}}+\frac{µ_{r1}\sin^2 \theta_0}{µ_0})$

<終>

電気学の演習問題ー＞

[電磁気学Ⅱ]演習問題電磁気学の内の電気学の部分の集大成もかねて,演習問題としました。ただし,この問題の答えはあっているとは限らないので,引用の際は,ご注意願います。...

問題7

問題7：
長さ10cm，断面積1cm^2の棒状磁性体を$x$軸上に配置し，$x$軸方向に磁化させたところ，$M=796i_x$[kA/m]となった。

(1) $x=15$cm，$y=0$cmの点の磁界$H_1$を求めよ。
(2) $x=5$cm，$x=0$cmの点の磁界$H_2$を求めよ。
(3) この棒磁石に$H=(0,0,1)$[A/m]を印加したときのトルク$T$を求めよ。

問題7解答

(1) 解答

磁荷$q_m$について，

$q_m=|M|S$

$H_1=\frac{q_m}{4\pi |r-r_+|^3}(r-r_+)+\frac{-q_m}{4\pi |r-r_-|^3}(r-r_-)$

$H_1=\frac{q_m}{4\pi}(\frac{(r-r_+)}{|r-r_+|^3}-\frac{(r-r_-)}{|r-r_-|^3})$

$H_1=\frac{|M|S}{4\pi}(\frac{(15\times 10^{-2}-5\times 10^{-2},0-0)}{|(15\times 10^{-2}-5\times 10^{-2},0-0)|^3}-\frac{(15\times 10^{-2}+5\times 10^{-2},0-0)}{|(15\times 10^{-2}+5\times 10^{-2},0-0)|^3})$

$H_1=\frac{|M|S}{4\pi}(\frac{(10 \times 10^{-2},0-0)}{|(10\times 10^{-2},0-0)|^3}-\frac{(20\times 10^{-2},0)
}{|(20\times 10^{-2},0)|^3})$

$H_1=\frac{796\times 10^3 10^{-4}}{4\pi}(\frac{(1,0)
}{10^{-2}}-\frac{(1,0)}{4 \times 10^{-2}})$

$H_1=\frac{23880}{16\pi}$[A/m]

(2) 解答

$H_2=\frac{796\times 10^3 10^{-4}}{4\pi}(\frac{(0-5\times 10^{-2},5\times 10^{-2}-0)}{|(0-5\times 10^{-2},5\times 10^{-2}-0)|^3}-\frac{(0+5\times 10^{-2},5\times 10^{-2}-0)}{|(0+5\times 10^{-2},5\times 10^{-2}-0)|^3})$

$H_2=\frac{79.6}{4\pi}(\frac{(-1,1)}{|50\sqrt{2}\times 10^{-4}|}-\frac{(1,1)}{|50\sqrt{2}\times 10^{-4}|})$

$H_2=(-\frac{7960}{\sqrt{2}\pi},0)$[A/m]

(3) 解答

$T=m\times B$

$T=q_m l i_x µ_0 \times H$

$T=796\times 10^{3}\times 10^{-4} \times 0.1 \times 4\pi \times 10^{-7} (1,0,0)\times (0,1,1)$

$≒10^{-5}(0,-1,1)$[Nm]

<終>

問題8

問題８：

右図のように真空中に比透磁率$µ_r$の球状磁性体(半径$a$)[m]を配置し，一様磁束密度$B_0$を印加した。球状磁性体の反磁界係数は，方向によらず$N=\frac{1}{3}$である。真空中に配置した磁気双極子モーメント$m’$の作る磁位は$\phi_m=\frac{m’・r}{4\pi　µ_0 r^3}$である。
(1) 磁性体内部の磁束密度$B_{in}$を求めよ。
(2) 磁性体外部の磁束密度$B$を求めよ。

問題8解答

(1) 解答

ここで，$H_d$について，反磁界係数$N=\frac{1}{3}$より

$H_d=-\frac{1}{3}M\tag{1}$

$H_{in}$について，

$H_{in}=H_{0}+H_{d}\tag{2}$

式(2)を式(1)に代入すると，

$H_{in}=H_{0}-\frac{1}{3}M$

$H_{in}=H_{0}-\frac{1}{3}(\frac{B_{in}}{µ_0}-H_{in})$

$H_{in}=H_{0}-\frac{1}{3}(µ_r-1)H_{in}$

$(\frac{2}{3}+\frac{1}{3}µ_r)H_{in}=H_0$

$H_{in}=\frac{3}{2+µ_r}H_0$

$µ_r µ_0 H_{in}=\frac{3}{2+µ_r} µ_r µ_0 H_0$

$B_{in}=\frac{3µ_r}{2+µ_r}B_0$[T]

(2) 解答

$\phi_m$を変形すると，

$\phi_m=\frac{m’・r}{4\pi　µ_0 r^3}=\frac{m’ \cos \theta}{4\pi µ_0 r^2}$

$H_d$について，

$H_d=-∇・\phi_m$を用いると，

$H_d=-\frac{\partial}{\partial r}\frac{ m’ \cos \theta}{4\pi µ_0 r^2} i_r-\frac{1}{r}\frac{\partial}{\partial \theta}\frac{ m’ \cos \theta}{4\pi µ_0 r^2} i_{\theta}$

$H_d=\frac{ m’ \cos \theta}{2\pi µ_0 r^3} i_r+\frac{ m’ \sin \theta}{4\pi µ_0 r^3} i_{\theta}$

$H$について，

$H=H_0+H_d$

$H=\underbrace{|H_0|i_x}_{極座標系に分解}+\frac{ m’ \cos \theta}{2\pi µ_0 r^3} i_r+\frac{ m’ \sin \theta}{4\pi µ_0 r^3} i_{\theta}$

$H=|H_0|\cos \theta i_r-|H_0|\sin \theta i_{\theta}+\frac{ m’ \cos \theta}{2\pi µ_0 r^3} i_r+\frac{ m’ \sin \theta}{4\pi µ_0 r^3} i_{\theta}$

よって，求める磁束$B$は，

$B=|B_0|\cos \theta i_r-|B_0|\sin \theta i_{\theta}+\frac{ m’ \cos \theta}{2\pi r^3} i_r+\frac{ m’ \sin \theta}{4\pi r^3} i_{\theta}$

(すまぬ，惰性がでました。)