$$\require{\cancel}$$
この記事を読むメリット
☑自動制御の問題を解くことができるようになる。
自動制御Ⅰ2017演習問題
問題1
問題1:
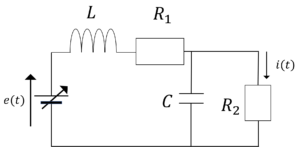
図の制御対象で,電圧\(i(t)\)を検出して,電源電圧\(e(t)\)を次式で制御する。
\(e(t)=K_p(i^*(t)-i(t))+K_i\int_{0}^{t}(i^*(t)-i(t))dt\)
ここで,\(K_p\),\(K_i\)は定数,\(i^*(t)\)は電流指令値である。
(1) 制御対象の伝達関数を求めよ。
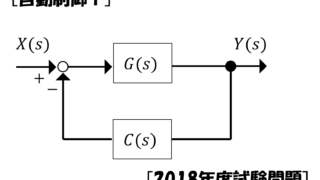
(2) 制御系全体のブロック線図を書け。
問題1解答
(1) 解答
回路図をラプラス表示すると,
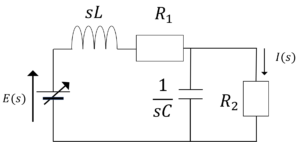
図1.ラプラス表示した回路図
図1.から伝達関数\(\frac{I(s)}{E(s)}\)は,
\(\frac{I(s)}{E(s)}=\frac{1}{\cancel{R_2}} \underbrace{\frac{\frac{\frac{1}{sC}\cancel{R_2}}{\frac{1}{sC}+R_2}}{sL+R_1+\frac{\frac{1}{sC}R_2}{\frac{1}{sC}+R_2}}}_{\frac{R_2I(s)}{E(s)}}\)
\(\frac{I(s)}{E(s)}=\frac{\frac{1}{sC}}{(sL+R_1)(\frac{1}{sC}+R_2)+\frac{1}{sC}R_2}=\frac{1}{(sL+R_1)(sCR_2+1)+R_2}\)
\(\frac{I(s)}{E(s)}=\frac{1}{s^2LCR_2+s(CR_1R_2+L)+R_1+R_2}\tag{1}\)
<終>

(2) 解答
\(e(t)=K_p(i^*(t)-i(t))+K_i\int_{0}^{t}(i^*-i(t))dt\)のラプラス変換
\( E(s)=K_p(I^*(s)-I(s))+\frac{K_i}{s}( I^*(s)-I(s)) \)
\( E(s)=(K_p+\frac{K_i}{s})( I^*(s)-I(s))\tag{2}\)
ここで,式(1),式(2)を使ってブロック線図を作図すると,
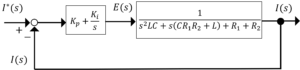
<終>
問題2
問題2:
次式で与えられる1次遅れ要素のナイキスト線図を求める式を導出し,\(\omega:0\rightarrow \infty\)に対する軌跡を図示せよ。
\(G(s)=\frac{1}{0.5+s}\)
問題2解答
\(G(s)=\frac{1}{0.5+s}\)
\(G(j\omega)=\frac{1}{0.5+j\omega}=\frac{2-4j\omega}{(1+2j\omega)( 1-2j\omega)}=\frac{2-4j\omega}{1+4\omega ^2}\)
ここで,\(G(j\omega)=x+jy\)とおくと,
\(x=\frac{2}{1+4\omega ^2},y=\frac{-4j\omega}{1+4\omega ^2}\)
\(\frac{y}{x}=-2\omega\)
\(x\)を\(\frac{y}{x}\)を使って表すと,
\(x=\frac{2}{1+(\frac{y}{x})^2}\)
\(x(1+(\frac{y}{x})^2)=2\)
\(x^2+y^2=2x\)
\((x-1)^2+y^2=1\)
上の式から,ナイキスト線図は,

図2.ナイキスト線図
<終>
問題3
問題3:
伝達関数が,\(G(s)=\frac{20(s+0.1)}{s(s+2)}\)であるとき,ボード線図の略図を書け。
(片対数グラフ上に線を書く。)
問題3解答
\(G(j\omega)=\frac{1+10j\omega}{j\omega(1+0.5j\omega)}\)
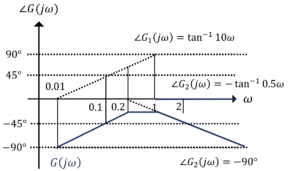

図2.ボード線図
問題4
問題4:
図のブロック線図で示される制御系で安定となる\(K\)の条件を求めよ。
問題4解答
まず,\(\frac{Y(s)}{U(s)}\)について求める。
\(\frac{Y(s)}{U(s)}=\frac{\frac{1}{s(s+1)}}{1+2\frac{1}{s(s+1)}}\)
\(\frac{Y(s)}{U(s)}=\frac{1}{s^2+s+2}\)
続いて,\(\frac{Y(s)}{R(s)}\)を求める。
\(\frac{Y(s)}{R(s)}=\frac{ K\frac{1}{s^2+s+2}}{1+\frac{1}{s+2}K\frac{1}{s^2+s+2}}\)
\(\frac{Y(s)}{R(s)}=\frac{ K}{ s^2+s+2+\frac{1}{s+2}K}\)
\(\frac{Y(s)}{R(s)}=\frac{ K(s+2)}{ (s^2+s+2)(s+2)+K}\)
\(\frac{Y(s)}{R(s)}=\frac{ K(s+2)}{ s^3+3s^2+4s+K+4}\tag{1}\)
ここで式(1)は,ラウスの安定判別法より,分母の係数は全て正なので,
\(K>-4\)
| \(s^3\) | 1 | 4 | 0 |
| \(s^2\) | 3 | K+4 | 0 |
| \(s^1\) | -\frac{K+4-12}{3}=\frac{8-K}{3} | 0 | 0 |
| \(s^0\) | -\frac{-(K+4)\frac{8-K}{3}}{\frac{8-K}{3}}=K+4 | 0 | 0 |
図3.ラウス表
ラウス表より,\(b_1>0\),\(c_1>0\)
\(b_1=\frac{8-K}{3}>0\)
\(K<8\) \(c_1=K+4>0\)
\(-4<K\)
よって,安定条件は,
\(-4<K<8\)
<終>
問題5
問題5:
図のブロック線図で示される制御系で,目標値が0から1に変化したときの出力のステップ応答を求めよ。

問題5解答
(1) 解答
\(r(t)\)は,単位ステップ関数なので,\(R(s)=\frac{1}{s}\)
従って,\(Y(s)\)は
\(Y(s)=\frac{1}{s}\frac{\frac{2(s+1)}{s^2+3s+4}}{1+2\frac{s+1}{s^2+3s+4}}\)
\(Y(s)=\frac{1}{s}\frac{2(s+1)}{s^2+5s+6}\)
\(Y(s)=\frac{1}{s}\frac{2(s+1)}{(s+2)(s+3)}\)
\(Y(s)=\frac{1}{3}\frac{1}{s}-\frac{1}{s+2}+\frac{4}{3}\frac{1}{s+3}\)
ここで,両辺を逆ラプラス変換すると,
\(y(t)=\frac{1}{3}-e^{-2t}+\frac{4}{3}e^{-3t}\)
<終>
関連記事
まとめ
ラプラス変換表->