とはいえ、問題は予想できそう。
電子物性問題1
炭素は原子番号6の元素であり,6つの電子を持っている。区別をつけるために,ここではそれぞれお電子1,電子2,\(\cdots\),電子6と表記する。電子の状態は4つの量子カ数により量子化されており,そのうちの1つが主量子数\(n\)である。残りの3つの量子化数は何か?下の表の(a)~(c)に解答せよ。また,炭素が持つ6つの電子の基底状態における各量子数の数値を下の表に示せ。(太枠部分を解答せよ)
| 主量子数\(n\) | (a) | (b) | (c) | |
| 電子1 | ||||
| 電子2 | ||||
| 電子3 | ||||
| 電子4 | ||||
| 電子5 | ||||
| 電子6 |
電子物性問題1解答
| 主量子数\(n\) | (a) 方位量子数\(l\) | (b) 磁気量子数\(m\) | (c)スピン量子数\(m_s\)/ | |
| 電子1 | 1 | 0 | 0 | \(\frac{1}{2}\) |
| 電子2 | 1 | 0 | 0 | \(-\frac{1}{2}\) |
| 電子3 | 2 | 0 | 0 | \(\frac{1}{2}\) |
| 電子4 | 2 | 0 | 0 | \(-\frac{1}{2}\) |
| 電子5 | 2 | 1 | -1 | \(\frac{1}{2}\) |
| 電子6 | 2 | 1 | 0 | \(\frac{1}{2}\) |
電子物性問題2
断面積5\(cm^2\)で,長さ1\(cm\)の円柱状のn型半導体がある。この半導体の長さ方向に電圧10Vを印加した。キャリア密度\(n\)が\(10^{22}\)[m^-3],移動度\(μ\)が\(10^{-3}\)であるとき,ドリフト速度の大きさ\(|v_d|\)を求めよ。
電子物性問題2解答
\(j=en|v_d|\)
\(|v_d|=\frac{μV}{d}\)
\(|v_d|=\frac{10^{-3}・10}{0.01}=1\)[m/s]
電子物性問題3
時間に依存しないシュレディンガー方程式は次式で与えられる。
\([ -\frac{\hbar^2}{2m}∇^2+U ] \phi=E \phi \)
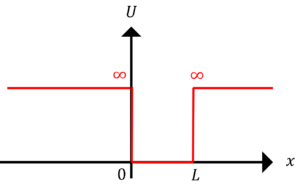
右図のような1次元の井戸型ポテンシャル内に電子を閉じ込めたとき,電子の(a)波動関数\(\phi\)と(b)基底状態のエネルギー\(E\)を求めよ。
電子物性問題3解答
(a)解答
\([ -\frac{\hbar^2}{2m}\frac{∂^2}{∂x^2}+U ] \phi=E \phi \)
\(-\frac{\hbar^2}{2m}\frac{∂^2}{∂x^2}\phi=(E-U)\phi\)
(ⅰ)\(x < 0,L\)
\(U=\infty\)より,
\(\phi=0\)
(ⅱ)\(0 \leq x \leq L\)
\(U=0\)より,
\(-\frac{\hbar^2}{2m}\frac{∂^2}{∂x^2}\phi=E\phi\tag{1}\)
\(\phi=C_1\cos k_x x+C_2\sin k_x x (∵k=\frac{\hbar}{\sqrt{2mE}})\)
波動関数\(\phi\)は連続なので,\(\phi(0)=0,\phi(L)=0\)
\(\phi(0)=C_1=0\)
\(\phi(L)=C_2 \sin k_x L=0\)
\(k_x=\frac{n_x \pi}{L}) (n_x=1,2,3,\cdots)\)より,\(\phi\)は,
\(\phi=C_2 \sin \frac{n_x \pi}{L}x (n_x=1,2,3,\cdots)\)
波動関数\(\int_{-\infty}^{\infty}|\phi|^2 dx=1\)より,
\(\int_{-\infty}^{\infty}|\phi|^2 dx=\int_{0}^{L}C_2^2\sin^2 k_x dx =1\)
\(C_2^2 \int_{0}^{L}\frac{1-\cos 2k_x}{2} dx =1\)
\(C_2^2 \frac{L}{2}=1\)
\(C_2=\sqrt{\frac{2}{L}}\)
\(\phi=\sqrt{\frac{2}{L}}\sin \frac{n_x \pi}{L}x (n_x=1,2,3,\cdots) \tag{2}\)
(b)解答
式(1)より,\(E\)は,
\(-\frac{\hbar^2}{2m}\frac{∂^2}{∂x^2}\phi=E\phi \)
式(2)を式(1)に代入すると,
\(-\frac{\hbar^2}{2m}\frac{∂^2}{∂x^2}\sqrt{\frac{2}{L}}\sin \frac{n_x \pi}{L}x =E \sqrt{\frac{2}{L}}\sin \frac{n_x \pi}{L}x \)
\(\frac{\hbar^2}{2m}(\frac{n_x \pi}{L})^2=E\)
\(\frac{h^2}{4\pi^2 2m}(\frac{n_x \pi}{L})^2=E\)
\(E=\frac{h^2}{8m}\frac{n_x^2}{L^2}\)
電子物性問題4
直方体状の半導体を用いて,右図のような回路を組み,ホール起電力を測定した。半導体の寸法や各電流・電流値は以下の通りである。
\(a=1cm,b=0.5cm,c=100μm,V=1.5V,I=12mA,\)
\(V_H(>0),B=0.1T\)
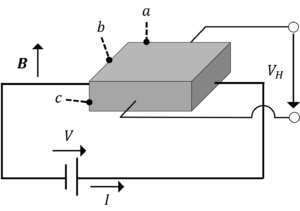
(2) この半導体のキャリア密度が\(10^{23}\)[m^-3]の時,\(V_H\)の値を求めよ。
(3) ホール効果を利用した磁束密度\(B\)の測定では,半導体の代わりに導体を用いることは困難である。その理由を述べよ。
電子物性問題4解答
n型半導体。
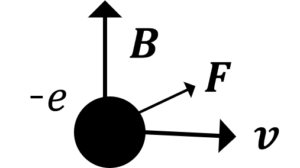
図1.電子が受けるローレンツ力
図2.ホールが受けるローレンツ力
ホール,電子ともに奥向きにローレンツ力を受けて,奥向きに移動する。
ホールの場合は奥向きに正の電位差が生じ,電子の場合は手前向きに正の電位差が生じる。
問題5の図において,手前向きに正の電位差が生じているので,半導体内の多数キャリアが電子であることがわかる。
(2)解答
ホール起電力\(V_H\)について,
\(V_H=vB b\)
キャリアの速度\(v\)について,
\(v=\frac{I}{en S}=\frac{I}{en bc}\)
以上の2式より,ホール起電力\(V_H\)は,
\(V_H=\frac{IB b}{enbc}=\frac{IB}{enc}\)
\(V_H=\frac{12×10^{-3}・0.1}{1.6×10^{-19}・10^{23}・100×10^{-6}}\)
\(V_H=7.5×10^{-4}\)V
(3)解答
導体は半導体に比べて電子密度がはるかに大きく,ホール起電力は極小になるので,測定に適さないから。
電子物性問題5
半導体内の電子密度\(n\)やホール密度\(p\)は,伝導体下端エネルギー\(E_C\),価電子帯上端エネルギー\(E_V\)およびフェルミエネルギー\(E_F\)を用いて近似的に以下の式で表すことができる。
\(n=N_C exp(-\frac{E_C-E_F}{k_B T}),p=N_v exp(\frac{E_C-E_F}{k_B T})\)
(1) 上式を利用し,真性フェルミ準位\(E_i\)を求めよ。(上式中の文字を用いて\(E_i\)を表せ\)
(2) Siよりも耐熱性が高いことや移動度が高いことから,GaAs(ガリウムひ素)も半導体としてよく用いられる。\(T=300\)KにおけるGaAsの真性キャリア密度\(n_i(=p_i)\)は\(2.00×10^{12}\)[m^-3]であり,GaAsの300Kにおける物性値は,\(N_c=4.70×10^{23}\)[m^-3],\(N_v=7.00×10^{24}\)[m^-3]である。GaAsのバンドギャップ\(E_g\)[eV]を求めよ。
(3) (2)のGaAsに\(1.00×10^{17}\)[m^-3]のP(リン)をドープした。この半導体の室温付近(300K)におけるホール密度\(p\)と電子密度\(n\)を求めよ。
(4) (3)の不純物半導体の室温付近(300K)におけるフェルミエネルギー\(E_F\)[eV]を求めよ。簡単のため,\(E_v\)をエネルギーの基準点(\(E=0\)のレベル)とし,GaAsのバンドギャップは(2)の計算値を利用せよ。
(5) この不純半導体の400Kの時のフェルミエネルギー\(E_F\)を求めよ。真性キャリア密度の計算に必要なGaAsの物性値(\(N_c,N_v,E_g\))は300Kのものをそのまま使って良い。
電子物性問題5解答
(1)解答
真性半導体のフェルミ準位を\(E_i\)なので,与えられた式の\(E_F\)を\(E_i\)に書きかえる。
\(n= N_cexp(-\frac{E_c-E_i}{k_BT})\)
\(p= N_vexp(\frac{E_v-E_i}{k_BT})\)
また,真性半導体ではホールと電子の数が一致するので,\(n=p\)が成立する。
\(n=p\)
\(N_cexp(-\frac{E_c-E_i}{k_BT})= N_vexp(\frac{E_v-E_i}{k_BT})\)
\(-\frac{E_c-E_i}{k_BT}-\frac{E_v-E_i}{k_BT}=\ln (\frac{N_v}{N_c})\)
\(E_i=\frac{1}{2}k_BT\ln (\frac{N_v}{N_c})+\frac{E_v+E_c}{2} \)
(2)解答
\(pn=n_i^2\)に\(n,p\)をそれぞれ代入すると,真性キャリア密度\(n_i\)は,
\(n_i^2=pn=N_vN_c exp(-\frac{E_g}{k_BT})\)
\(E_g=k_BT\ln (\frac{N_vN_c}{n_i^2})\)[J]
\(E_g=\frac{1.381×10^{-23}}{1.602×10^{-19}}・300・\ln (\frac{4.7×10^{23}・7.00×10^{24}}{(2.00×10^{12})^2})=1.43\)[eV]
(3)解答
\(n=N_D+n_i≒N_D\)
\(n=1.00×10^{17}\)[m^-3]
\(p=\frac{n_i^2}{p}=4.0×10^{7}\)[m^-3]
(4)解答
価電子帯上端エネルギー\(E_v\)を基準とすると,
\(p=N_v exp(\frac{E_v-E_F}{k_BT})= N_v exp(\frac{-E_F}{k_BT})\)
よって,\(E_F\)は,
\(E_F=k_BT\ln (\frac{N_v}{p})\)[J]
\(E_F=\frac{1.381×10^{-23}}{1.6×10^{-19}}・300・\ln (\frac{7.00×10^{24}}{4.0×10^{7}})=1.03\)eV
(5)解答
真性キャリア密度\(n_i\)は,
\(n_i=\sqrt{N_vN_c exp(-\frac{E_g}{k_BT})}\)
\(n_i=\sqrt{4.7×10^{23}・7×10^{24}exp(-\frac{1.43・1.6×10^{-19}}{1.381×10^{-23}・400})=1.84×10^{15}}\)
\(n=\frac{N_D+\sqrt{N_D^2+n_i^2}}{2}≒N_D\)より,ホール密度\(p\)は,(3)とほぼ等しくなる。
よって,\(E_F\)は,
\(E_F=\frac{1.381×10^{-23}}{1.6×10^{-19}}・400・\ln (\frac{7.00×10^{24}}{4.0×10^{7}})=1.37 \)eV
電子物性問題6
p型半導体(アクセプタ密度\(N_A\))とn型半導体(ドナー密度\(N_D\))を組み合わせて,pn接合(ダイオード)を作製した。断面積は両半導体とも\(S\)とする。
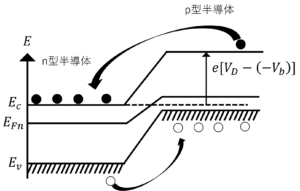
(1) pn接合前後の室温付近でのバンド図を示せ。バンド図では\(E_c,E_v,E_F,E_A\)(アクセプタ準位),\(E_D\)(ドナー準位)は最低限示せ。電子を●,ホールを○とし,接合面に対して左側をn型半導体とし,電子の基準はn形半導体側とする。
(2) pn接合面には電荷が蓄えられ,拡散電位\(V_D\)が生じているため,コンデンサのようにふるまう。pn接合面の静電容量を求めよ。半導体の誘電率\(\varepsilon \)とする。
(3) 一般的なダイオードは右図のようなI-V特性を持つ。実際のダイオードは電流が大きく流れるために,ある程度の大きさの電圧を印加する必要(①の状態)がある。その理由を説明せよ。
(4) 理想的なダイオードは一方向にしか電流を流さないが,実際のダイオードはバイアス時にも電流が流れる。逆バイアス時の電流をゼロにできない(②の状態)理由を述べよ。
(5) 実際のダイオードは半導体に電流を流すための金属電極を接続する必要があるので,pn接合面以外に金属と半導体の接合面も存在する。金属とn型半導体の接合前後の室温付近でのバンド図を示せ。電位の基準は導体側とする。
(6) 金属と半導体を単純に接合しただけでは,実応用面で問題が生じることが多い。考えられる問題点とその対策を述べよ。
電子物性問題6解答
(1)解答
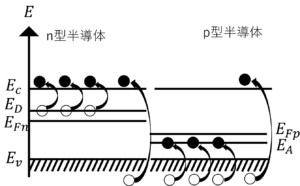
図3.pn接合前のバンド図
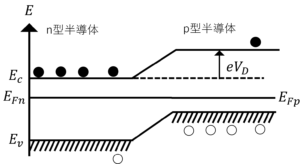
図4.pn接合後のバンド図
(2)解答
\(C_d=\frac{dQ}{dV_d}\tag{1}\)
pn接合面に蓄えられる電荷\(Q\)は,
\(Q=eN_D S l_n\tag{2}\)
で表される。ここで,n型半導体の空乏層の長さ\(l_n\)を求める。
(ⅰ)\(x \leq 0\)の領域において,
\(\frac{∂^2}{∂x^2}=-\frac{∂E(x)}{∂x}・i_x=-\frac{eN_D}{\varepsilon}\)
が成立する。\(E(x)\),\(V(x)\)はそれぞれ積分すると,
\(E(x)=\frac{eN_D}{\varepsilon}(x+l_n)i_x (∵E(-l_n)=0)\)
\(V(x)=-\frac{eN_D}{2\varepsilon}(x+l_n)^2 (∵V(-l_n)=0)\)
(ⅱ)\(x \geq 0\)の領域において,
\(\frac{∂^2}{∂x^2}=-\frac{∂E(x)}{∂x}・i_x=-\frac{-eN_A}{\varepsilon}\)
が成立する。\(E(x)\),\(V(x)\)はそれぞれ積分すると,
\(E(x)=-\frac{eN_A}{\varepsilon}(x-l_p)i_x (∵E(l_p)=0)\)
\(V(x)=\frac{eN_A}{2\varepsilon}(x-l_p)^2-\frac{e}{2\varepsilon}(N_Dl_n^2+N_Al_p^2) (∵V(0)= -\frac{eN_D}{2\varepsilon}l_n^2)\)
\(V_d=|V(l_p)|= \frac{e}{2\varepsilon}(N_Dl_n^2+N_Al_p^2)\tag{3}\)
電束密度の境界条件より,\(\varepsilon E(-0)・i_x=\varepsilon E(+0)・i_x\)が成立する。
\(eN_Dl_n=-eN_A(-l_p)\)
\(N_Dl_n=N_Al_p\tag{4}\)
式(3),式(4)を連立させると,\(l_n\)が求まる。
\(V_d=\frac{e}{2\varepsilon}(N_Dl_n^2+\frac{N_D^2}{N_A}l_n^2)\)
\(l_n=\sqrt{\frac{2\varepsilon}{e(N_A+N_D)}\frac{N_A}{N_D}V_d}\tag{5}\)[m]
\(l_p=\sqrt{\frac{2\varepsilon}{e(N_A+N_D)}\frac{N_D}{N_A}V_d}\)
空乏層の幅を\(l_d\)とすると,
\(l_d=l_n+l_p=\sqrt{\frac{2\varepsilon}{e(N_A+N_D)}V_d}\sqrt{\frac{N_A}{N_D}+\frac{N_D}{N_A}}\)
\(l_d=\sqrt{\frac{2\varepsilon(N_A+N_D)}{eN_AN_D}V_d}\)
Pn接合面に蓄えられる電荷\(Q\)は式(2)に式(5)を代入すると求まるので,
\(Q=eN_D S \sqrt{\frac{2\varepsilon}{e(N_A+N_D)}\frac{N_A}{N_D}V_d}\)
\(Q=S \sqrt{\frac{2e \varepsilon N_AN_D}{N_A+N_D}V_d}\tag{6}\)
静電容量\(C_d\)は,式(1)に式(6)を代入すると求まるので,
\(C_d= S \sqrt{\frac{2e \varepsilon N_AN_D}{N_A+N_D}}\frac{d}{dV_d}\sqrt{V_d}\)
\(C_d=S\sqrt{\frac{2e \varepsilon N_AN_D}{N_A+N_D}}\frac{d}{dV_d}\frac{1}{2\sqrt{V_d}}\)
\(C_d=\varepsilon S \underbrace{\sqrt{\frac{eN_AN_D}{2\varepsilon(N_A+N_D)V_d}}}_{\frac{1}{l_d}}\)
\(C_d=\varepsilon \frac{S}{l_d}\)[F]
(3)解答
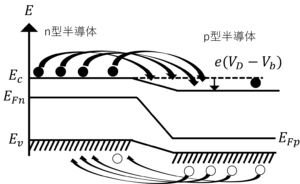
ダイオードに大きな電流を流すためには,多数キャリアが動けるようにpn接合部のエネルギー障壁を低くする必要がある。pn接合部のエネルギー障壁を低くするためには,順バイアスを\(V_d\)以上かけると,多数キャリアが動けるようになり,ダイオードに大きな電流を流すことができる。
(4)解答
半導体内にわずかに存在する少数キャリアがエネルギーの低い方に流れ込むことで,電気伝導を担うから。
(5)解答
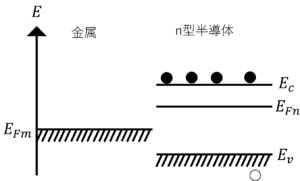
図5.金属と\(n\)型半導体の接合前
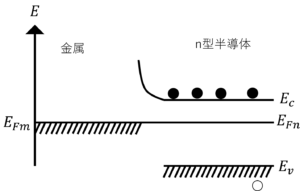
図6.金属と\(n\)型半導体の接合後
(6)解答
金属とn型半導体の接合部のエネルギー障壁が抵抗となって,望まぬ損失が出てくる。
これを阻止するには,n型半導体側の空乏層の幅を小さくし,トンネル効果を利用して電子を伝導させればいい,具体的には,金属の接合部に近いn型半導体のドナー密度を濃くするなどの対策が挙げられる。
最後に
ポケモン剣盾の机上論を新たに提唱します。ポケモンに努力値を効率的に振りたいよなぁ。
ポケモン方程式の発展版の公式をラグランジュ未定係数法から編み出しました。更に,努力値を効率的に振れるポケモンを探す為のプログラムを編み出したので,導出に興味がある人は楽しみにしていてください。(近日中にアップロードするネタです。)
オワオワリで~す🌟