どうも,ユキです。
明日死ぬかもしれないと過度に怯えていた時期がありませんでしたか?
今日は,死ぬことに怯えるのは杞憂であることを証明していこうと思います。
この記事を読むメリット
☑あなたが明日死ぬ確率がわかる(恐怖)
☑死ぬ確率を計算する方法がわかる
死ぬ確率を求めるにあたって
平成30年度現在の平均寿命(0歳児の平均余命)は,
男性:81.25年
女性:87.32年
となっています。平均寿命は,医療の発達に伴い上昇傾向にあり,現在は「人生100年時代」と呼ばれ,
人間が100年生きることが当たり前の時代になるだろうと言われています。
しかし,そこで私が「待った」をかけます。
今回は,本当に人間は100年間生きることができるのか?ということを
確率を用いて考察します。
死ぬ確率を関数化
まず,死ぬ確率を関数化してみましょう。
その為には,データが必要ですね。データを用意します。
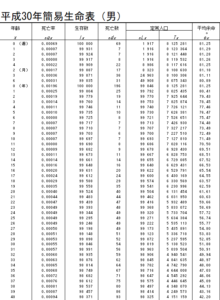
これは,簡易生命表と呼ばれるもので,1年の間に死亡する確率を1~105歳までまとめたものになります。
平成30年度の厚生労働省のページから引用しました。
このデータを用いて,男性が1年の間に死ぬ確率\(p_{my}(x)\)と女性が1年の間に死ぬ確率\(p_{wy}(x)\)の近似式求めます。
\(x\)には,任意の年齢を代入してください。
ここでは,計算を簡単にする為に指数近似を使います。(多項式近似だと,計算が複雑。)
すると,\(p_{my}(x)\),\(p_{wy}(x)\)はそれぞれ,
男性が1年間に死ぬ確率:
\(p_{my}(x)=3×10^{-5}e^{0.085x}\tag{1}\)
女性が1年間に死ぬ確率:
\(p_{my}(x)=5×10^{-5}e^{0.086x}\tag{2}\)
\(e≒2.718\)くらい
と求まります。\(e\)はネイピア数と呼ばれる無理数で,おおよそ2.718くらいです。
ちなみに,式(1)と式(2)は,普通の電卓では計算出来ないです。
計算をするには,2500円くらいの関数電卓(三角関数,自然対数,指数,階乗,積分までできる)かパソコンかスマホの電卓が必要です。
自然対数を覚えたくない人向けの記事->

さて,1年間で死ぬ確率を男性と女性で近似式を出しましたが,簡易生命表の値と少ーーしズレてしまいました。
\(p_{wy}(x),p_{my}\)の実際の確率とのズレは以下の通りです。
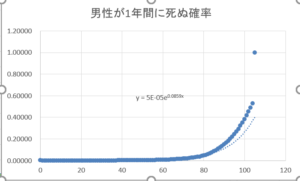
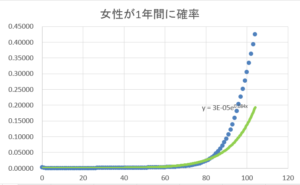
図1.死ぬ確率の近似曲線(左)男性が1年間に死ぬ確率.(右)女性が1年間に死ぬ確率.
年齢が高くなるにつれて,近似精度が悪くなっているのが見て取れますね。
でも計算には問題ないでしょう!
さて,この関数を用いて,人間が\(n\)歳まで生き残る確率を計算します。
何歳で死ぬ確率が100%になるのか?

\(n\)歳で死ぬ確率\(T(n)\)の求め方は,余事象を使い,\(n\)歳まで生き残る確率\(1-T(n)\)を求めるところから始まります。
0歳まで生き残り∩1歳まで生き残り∩\(\cdots\)∩\(n-1\)歳まで生き残り∩\(n\)歳まで生き残る確率が\(1-T(n)\)なので,
\(1-T(n)=(1-p(0))・(1-p(1))・\cdots・(1-p(n-1))・(1-p(n))= \prod_{k=0}^{n}1―p(k)\)
\(\prod_{k=0}^{n}\)は,0~\(n\)までかけ合わせるという意味です。
とかけます。よって,求める確率\(T_n\)は,
\(T(n)=1-\prod_{k=0}^{n}(1-p(k))\)
ここで,\(p(k)\)は,式(1),式(2)から\(p(k)=\beta e^{\alpha k}\)とおけるので,
\(T(n)=1-\prod_{k=0}^{n}(1-\beta e^{\alpha k})\)
となります。ここで,\(T(n)\)に関して\(\beta e^{\alpha k}≒0\)より,\(T(n)\)を1次近似すると,
\(T(n)≒1-1-\sum_{k=1}^{n}\beta e^{\alpha k}=\beta \frac{e^{\alpha (n+1)}-1}{e^{\alpha}-1}\tag{3}\)
となり,\(T(n)\)が求まりました。
\(n\)歳に死ぬ確率

式(3)を使って,男性と女性が\(n\)歳に死ぬ確率をそれぞれ計算しましょう。
男性が\(n\)歳に死ぬ確率\(T_m(n)\):
\(T_m(n)=5.0×10^{-5}e^{0.086 n}\tag{4}\)
女性が\(n\)歳に死ぬ確率\(T_w(n)\):
\(T_w(n)=3.0×10^{-5}e^{0.085 n}\tag{5}\)
実際に式(4),式(5)に当てはめて計算すると,以下のようになります。
| 女性が死ぬ確率 | 男性が死ぬ確率 | |
| 20歳 | \(1.51×10^{-3}\) | \(2.55×10^{-3}\) |
| 30歳 | \(3.99×10^{-3}\) | \(6.79×10^{-3}\) |
| 40歳 | \(9.79×10^{-3}\) | \(1.68×10^{-2}\) |
| 50歳 | \(2.34×10^{-2}\) | \(4.05×10^{-2}\) |
| 60歳 | \(5.51×10^{-2}\) | \(9.64×10^{-2}\) |
| 70歳 | \(0.129\) | \(0.229\) |
驚くべきことに,40歳になったら100人中1人はこの世を去っているという結果が得られました。
宝くじに当選する確率よりも高い確率で,先立ってしまわれるかたもいらっしゃるのは意外でした。
そして,見てわかるとおり,女性の方が男性に比べて死ぬ確率は低いと言うことも読み取れます。女性の方が長生きなんですね。
日本人の最高寿命を計算

ここで,話は変わりますが,日本人の最高の寿命を知りたくないですか?
先ほど求めた,\(T(n)\)が1未満となる最大の\(n\)が日本人の最高の寿命になります。
まず,式(3)を変形しましょう。
\(T(n)=\beta \frac{e^{\alpha (n+1)}-1}{e^{\alpha}-1}\)
ここで,\(T(n) < 1\)より,
\(\beta \frac{e^{\alpha (n+1)}-1}{e^{\alpha}-1} \geq 1\)
これを整理すると,
\( n < \frac{ln{ \frac{e^{\alpha}-1}{\beta}+1}}{\alpha}-1\tag{6}\)
となります。
\(\beta,\alpha\)に適当な値を代入すると,
男性の最高年齢:
\(n < \frac{ln {\frac{e^{0.086}-1}{5×10^{-5}}+1}}{0.086}-1=86.14歳\)
男性最高:86歳
女性の最高年齢:
\( n < \frac{ln {\frac{e^{0.085}-1}{3×10^{-5}}+1}}{0.085}-1=93.03歳\)
女性最高:93歳
\(e≒2.718\)くらい
男性の最高年齢は86歳,女性最高は93歳となりました。
う~ん。この結果は妥当なのでしょうか?
聞けば,年齢が100歳を超える方もいらっしゃるようです。なので,この結果は正しくないという事は一目瞭然です。
このような結果になった理由としては,死ぬ確率\(p_{wy}(x),p_{my}(x)\)と実際の値との誤差が上げられます。
式(1)と式(2)は指数近似といって,結構荒っぽく近似をしています。
実際,真値と関数との誤差率が60%を超えるところもありました。
近似精度の高い関数は真値との誤差率が0近くなります。しかしながら,精度を上げると関数が複雑化してしまい,計算が複雑になります。
つまり,近似精度と関数の複雑さはトレードオフの関係にあるということです。
正しい値を求めたいという方は,厚生労働省の簡易生命表を参考に計算してみてください。
明日死ぬ確率

最後に,明日死ぬ確率を近似的に求めましょう。
式(1)と式(2)に工夫を加えることで,生後\(x\)日に男性が次の日に死ぬ確率\(p_{md}(x)\)と,生後\(x\)日に女性が次の日に死ぬ確率\(p_{wd}(x)\)が求まります。
生後\(x\)日に男性が次の日に死ぬ確率:
\(p_{md}(x)=\frac{5×10^{-5}}{365.24}e^{\frac{0.086}{365.24}x}\tag{7}\)
生後\(x\)日に女性が次の日に死ぬ確率:
\(p_{wd}(x)= \frac{3×10^{-5}}{365.24}e^{\frac{0.085}{365.24}x}\tag{8}\)
式(7)と式(8)に自分が生きてきた日にちを代入すると,明日死ぬ確率が求まります。
ちなみに,私(男:19歳)の明日死ぬ確率\(p_{md}(7260)\)は,
\(p_{md}(7260)=7.56×10^{-7}\)
1000万人中7.6人が死ぬレベルの確率でした。(めちゃくちゃ低い!)
明日死ぬ確率:まとめ
男性が1年間に死ぬ確率:
\(p_{my}(x)=3×10^{-5}e^{0.085x}\tag{1}\)
女性が1年間に死ぬ確率:
\(p_{my}(x)=5×10^{-5}e^{0.086x}\tag{2}\)
生後\(x\)日に男性が次の日に死ぬ確率:
\(p_{md}(x)=\frac{5×10^{-5}}{365.24}e^{\frac{0.086}{365.24}x}\tag{7}\)
生後\(x\)日に女性が次の日に死ぬ確率:
\(p_{wd}(x)= \frac{3×10^{-5}}{365.24}e^{\frac{0.085}{365.24}x}\tag{8}\)
最後に
好奇心から明日死ぬ確率を計算してみました。自分が生まれて今まで生きている事は,奇跡でも何でもなく,割と普通であることがわかりました。まあ,これは日本人に限った話であって,海外では違った結果が出るでしょう。