$$\require{\cancel}$$
大学生で金欠はきついですね。遊びたいけれど金がなさすぎて遊ぶ気が失せます。
就活のための資金と1週間旅行にいけるだけの金額が貯まるまで金は使いたくないですね。
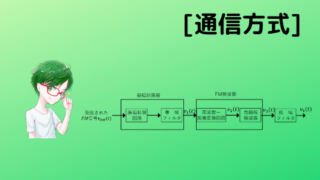
さて,今日は,アナログ変調とディジタル変調の間であるパルス変調について学習していきましょう。
問題1
標本化定理について説明しなさい。
問題1解答
$$v(t)=\sum_{n=-\infty}^{\infty}v(\frac{n}{2f_m}) S_a[2\pi f_m(t-\frac{n}{2f_m})]$$
最高周波数\(f_m\)に制限された信号は,時間間隔\(T\leq \frac{1}{2f_m}\)ごとに抽出した標本によって完全に表現できる。
問題2
パルス振幅変調信号の振幅レベルは連続値をとるから,伝送路において雑音が加わると元の信号波形を再現するのは難しい。従って,情報信号のとる連続値をその値に最も近い利産地で置き換え,離散レベルを伝送することにすれば,受信側では極端な雑音が加わらない限り信号を識別することはずっと容易になる。このように連続値を近似的に離散値で(c1)化し,その値をさらに1,0,等の少数のパルスの組み合わせ
で(c2)化する変調方式を(c3)変調という。しかし,いったん(c1)されたら離散的信号から連続的信号を復元することはできず,避けられないひずみを伴う。これは一種の雑音であり,(c4)と呼ばれる。
問題2解答
(c1) 量子,(c2)符号,(c3)パルス符号,(c4)量子化雑音
問題3
振幅\(A\),時間幅\(τ\),周期\(T\)の方形パルス列によって自然標本化されたPAM信号は
$$V_{PAM}(t)=\frac{Aτ}{T}\sum_{n=-\infty}^{n=\infty}S_a(\frac{n\pi τ}{T})v(t)exp(j\frac{2n\pi}{T}t)$$
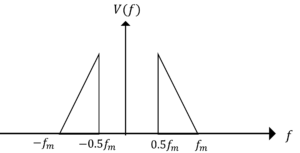
と表すことができる。ここで,\(S_a(t)\)は標本化関数,また\(v(t)\)は情報信号であり,下図のような周波数スペクトル\(V(f)\)を持つ。図中の\(f_m\)は情報信号の最高周波数であり,\(f_m=\frac{1}{2T}\)である。このときの\(V_{PAM}(f)\)の周波数スペクトル表現式を求め,その分布を図示せよ。
問題3解答
PAM信号をフーリエ変換すると,
\(V_{PAM}(f)= \frac{Aτ}{T}\sum_{n=-\infty}^{n=\infty}S_a(\frac{n\pi τ}{T}) \int_{-\infty}^{\infty} v(t)exp(j\frac{2n\pi}{T}t) exp(-j\frac{2\pi}{T}t)dt\)
\(V_{PAM}(f)= \frac{Aτ}{T}\sum_{n=-\infty}^{n=\infty}S_a(\frac{n\pi τ}{T}) \int_{-\infty}^{\infty} v(t)exp(-j\frac{2(1-n)\pi}{T}t)dt\)
\(V_{PAM}(f)= \frac{Aτ}{T}\sum_{n=-\infty}^{n=\infty}S_a(\frac{n\pi τ}{T}) V(f-\frac{n}{T}) \)
PAM信号のスペクトル分布は,作図が面倒なので省略する。
問題4
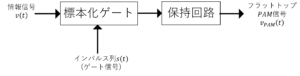
下図はフラットトップ標本化PAM信号発生のブロック図を示したものである。各素子は以下の働きをする。
・標本化ゲート;情報信号を入力し,インパルス列を用いた標本信号\(v_{s}(t)\)を出力する。
・保持回路:インパルスを入力し,方形パルス\(p(t)\)を出力する。
このフラットトップ標本化について以下の問に答えよ。
(1) 時間領域でのフラットトップ\(PAM\)信号は\(v_{PAM}(t)=v_{S}(t)❎p(t)\)と表される。ここで❎は「畳込み」を表す,\(V_{S}(t),p(t)\)の周波数スペクトル密度を\(V_{S}(f),P(f)\)とするとき,フラットトップ\(PAM\)信号の周波数スペクトル密度\(V_{PAM}(f)\)はどのような式で表されるか答えよ。
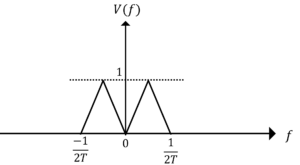
\(V(f)\)のスペクトル分布
(2) \(V_{S}(f)\frac{1}{T}\sum_{n=-\infty}^{\infty}V(f-\frac{n}{T}),P(f)=S_a(kf)\)とする。ここで,関数\(V(f)\)は図2のようにあらわされ,\(T\)は周期を表す。また,\(S_a(x)\)は標本化関数であり,\(k\)はパルス幅等で決まる定数である。このとき\(V_{S}(f),P(f)\)を図示せよ。ただし,\(P(f)\)の範囲は\(-2\pi \leq kf \leq 2\pi\)とする。
(3) 上記問題①,②を利用し,\(-\pi \leq kf\leq\pi\)の範囲で\(V_{PAM}(f)\)を図示せよ。
問題4解答
①解答
\(v_{PAM}(t)=v_{S}(t)❎p(t)\)
両辺をフーリエ変換すると,
\(V_{PAM}(f)=V_{S}(f)P(f)\)
②解答
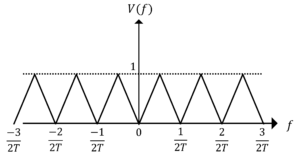
\(V_s(f)\)のスペクトル分布->
\(V_s(f)\)のスペクトル分布
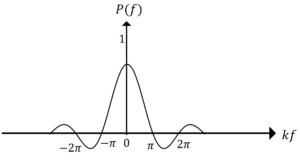
\(P(f)\)のスペクトル分布->
\(P(f)\)のスペクトル分布
③解答
\( V_{PAM}(f)=V_{S}(f)P(f)\)
を用いると求められる。図は省略する。
最後に
PAM信号は,自然標本化とフラットトップ標本化の2種類の変調方法があったので,それらの区別をできるように頑張りましょう。