$$\require{\cancel}$$
どうも,ユキです。ここ2年,ノートを買っていないですが,講義資料の裏紙だけで何とか耐えています。
そんなことはどうでもいいので,早速FM信号に関する問題を解いていきましょう。
問題1
単一周波数\(f_m\)の正弦波で周波数変調信号が
$$v_{FM}=A\cos [2\pi f_ct+\beta \sin (2\pi f_mt)] (\beta=2)$$
で表されるとき,以下の問に答えよ。
(1) 無変調搬送波の電力\(P_C\)を求めよ。ただし,電力は\(P=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}v^2(t)dt\)として定義される。
(2) 以下のことを利用し,\(n=2\)までの周波数変調された信号の電力伝送効率を求めよ。
※(1),(2)のヒント
・周波数変調信号の電力は変調指数に無関係で,無変調搬送波の電力に等しい。
・周波数変調信号の電力は\(P_2=\frac{A^2}{2}[J_0^2(\beta)+2J_1^2(\beta)+2J_2^2(\beta)]\)と表される。
・\(J_0(2)=0.2239,J_1(2)=0.5767,J_2(2)=0.3528\)
問題1解答
(1)解答
周波数変調信号の電力\(P_c\)は,無変調搬送波の電力に等しいので,無変調搬送波の電力について考える。
無変調搬送波\(v(t)=A\cos (2\pi f_c t)\)より,求める電力\(P_c\)は,
\(P_c=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} {A\cos (2\pi f_c t)}^2dt\)
\(P_c=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} A^2\frac{1+\cos (4\pi f_c t)}{2}dt\)
\(P_c=\frac{A^2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} \frac{1+\cos (4\pi f_c t)}{2}dt\)
\(P_c=\frac{A^2}{T}\frac{T}{2}=\frac{A^2}{2}\)
(2)解答
伝送効率\(η\)について,側波帯の電力\(P_{S}\)を搬送波帯の電力\(P_c\)で割ったものなので,
\(η=\frac{P_{S}}{P_c}=\frac{\frac{A^2}{2}[J_0^2(\beta)+2J_1^2(\beta)+J_2^2(\beta)]}{\frac{A^2}{2}}\)
\(η=J_0^2(\beta)+2J_1^2(\beta)+2J_2^2(\beta)=0.2239^2+2×0.5767^2+2×0.3528^2≒0.964\)
問題2
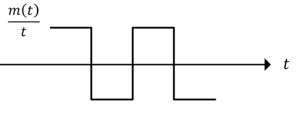
以下に示す三角パルスのPM波形を描け。
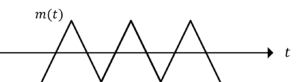
三角パルス波
問題2解答
PM波形は次式で定義されている。
\(v_{PM}(t)=A\cos [2\pi f_c t+K_P \int_{-\infty}^{t}m’(t)dt]\)
\(v_{PM}(t)=A\cos \underbrace{[2\pi f_c t+K_P m(t)]}_{振動数の部分をグラフにする}\)
\(\frac{m(t)}{t}\)の波形は,
となる。\(v_{PM}(t)\)の振動数の波形(\(v_{PM}(t)\)の三角関数の中身)は
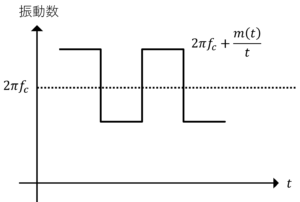
よって,\(v_{PM}(t)\)の波形は,
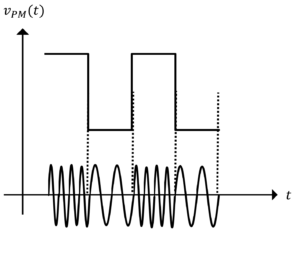
問題3
単一周波数\(f_m\)の正弦波で周波数変調された信号が
$$v_{FM}(t)=A\cos [2\pi f_c t+\beta \sin(2\pi f_m t)] \beta≪1$$
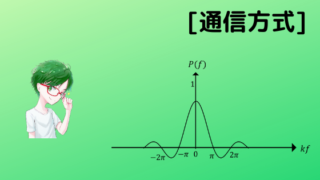
で表されるときの周波数スペクトルの表現式とそのスペクトル分布を図示せよ。
問題3解答
\(v_{FM}(t)=A\cos [2\pi f_ct+\beta \sin (2\pi f_m t)]\)
\(v_{FM}(t)=A\cos (2\pi f_ct)\cos [\beta \sin (2\pi f_m t)]- A\sin (2\pi f_ct)\sin [\beta \sin (2\pi f_m t)]\)
\(\beta ≪1 \)より,
\(v_{FM}(t)=A\cos (2\pi f_ct)- A\sin (2\pi f_ct)\beta \sin (2\pi f_m t)\)
\(v_{FM}(t)=A\cos (2\pi f_ct)-\frac{A\beta}{2}\cos (2\pi (f_c-f_m))t)+ \frac{A\beta}{2}\cos (2\pi(f_c+f_m )t)]\)
両辺をフーリエ変換すると,
\(V_{FM}(f)=\frac{A}{2}[\delta (f-f_c)+\delta(f+f_c)]\)
\(+\frac{A \beta}{4}(\delta (f-f_c-f_m)+\delta (f+f_c+f_m)-\delta (f-f_c+f_m)+\delta (f+f_c-f_m))\)
※\(\delta (t)\)は,デルタ関数と呼ばれる特殊関数
よって,スペクトル分布は,
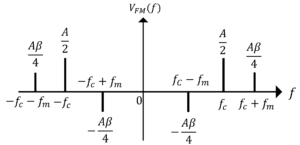
※補足
\(x\)が限りなく0に近い場合,マクローリン展開の1次の項に近似できる。
\(\cos x≒1,x ≒0\)
\(\sin x≒x,x ≒0\)
問題4
単一周波数\(f_m\)の正弦波で周波数変調された信号が
$$ v_{FM}(t)=A\cos [2\pi f_c t+\beta \sin(2\pi f_m t)] (\beta=2)$$
で表されるときの周波数スペクトルの表現式公式
$$\cos (\beta \sin x)=J_0(\beta)+2\sum_{n=1}^{\infty}J_{2n}(\beta)\cos (2nx)$$
$$\sin (\beta \sin x)=2\sum_{n=0}^{\infty}J_{2n+1}(\beta)\sin {(2n+1)x}$$
を利用して導出せよ。また\(n=2\)までのスペクトル分布を図示せよ。ここで,\(J_0(2)=0.2239,J_1(2)=0.5767,J_2(2)=0.3528\)である。
問題4解答
\( v_{FM}(t)=A\cos [2\pi f_ct+\beta \sin (2\pi f_m t)]\)
\( v_{FM}(t)=A\cos (2\pi f_ct)\cos [\beta \sin (2\pi f_m t)]-A\sin (2\pi f_ct)\sin [\beta \sin (2\pi f_m t)]\)
\( v_{FM}(t)=A\cos (2\pi f_ct) [J_0(\beta)+2\sum_{n=1}^{\infty}J_{2n}(\beta)\cos (4n\pi f_mt)]\)
\(-A\sin (2\pi f_ct)[ 2\sum_{n=0}^{\infty}J_{2n+1}(\beta)\sin {(2n+1) 2\pi f_mt }]\)
\( v_{FM}(t)=J_0(\beta) A\cos (2\pi f_ct)+2A\sum_{n=1}^{\infty}J_{2n}(\beta)\cos (4n\pi f_mt) \cos (2\pi f_ct)\)
\(-2A\sum_{n=0}^{\infty}J_{2n+1}(\beta)\sin {(2n+1) 2\pi f_mt }\sin (2\pi f_ct)\)
\( v_{FM}(t)=J_0(\beta) A\cos (2\pi f_ct)+A\sum_{n=1}^{\infty}J_{2n}(\beta)[\cos {(f_c+2nf_m)2\pi t}+\cos {(f_c-2nf_m)2\pi t}]\)
\(+A\sum_{n=0}^{\infty}J_{2n+1}(\beta)[\cos {(f_c+(2n+1)f_m)2\pi t}-\cos {(f_c-(2n+1)f_m)2\pi t}]\)
両辺をフーリエ変換すると。
\( V_{FM}(f)=\frac{AJ_0(\beta)}{2} {\delta (f-f_c)+\delta (f+f_c)}\)
\(+\frac{A}{2}\sum_{n=1}^{\infty}J_{2n}(\beta)[ {\delta (f-{f_c+2n f_m})+\delta (f+{f_c+2n f_m})}+ {\delta (f-{f_c-2n f_m})+\delta (f+{f_c-2n f_m})}]\)
\(-\frac{A}{2}\sum_{n=0}^{\infty}J_{2n+1}(\beta)[ \delta (f-(f_c+(2n+1)f_m))+\delta (f+(f_c+(2n+1)f_m))- \delta (f-(f_c-(2n+1)f_m))-\delta (f+(f_c-(2n+1)f_m))]\)
\(\beta =2\)を代入すると,
\( V_{FM}(f)=\frac{AJ_0(2)}{2} [\delta (f-f_c)+\delta (f+f_c)]\)
\(+\frac{A}{2}\sum_{n=1}^{\infty}J_{2n}(2)[ \delta (f-(f_c+2n f_m))+\delta (f+(f_c+2n f_m))+ \delta (f-(f_c-2n f_m))+\delta (f+(f_c-2n f_m))]\)
\(-\frac{A}{2}\sum_{n=0}^{\infty}J_{2n+1}(2)[ \delta (f-(f_c+(2n+1)f_m))+\delta (f+(f_c+(2n+1)f_m))- \delta (f-(f_c-(2n+1)f_m))-\delta (f+(f_c-(2n+1)f_m))]\)
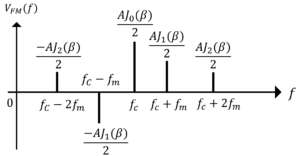
題意より,\(n=2\)まで書き下すと,
\( V_{FM}(f)≒\frac{AJ_0(2)}{2} [\delta (f-f_c)+\delta (f+f_c)]\)
\(+\frac{AJ_1(2)}{2} [\delta (f-(f_c+f_m))+\delta (f+(f_c+f_m))-\delta (f-(f_c-f_m))+\delta (f+(f_c-f_m))]\)
\(+\frac{AJ_2(2)}{2} [\delta (f-(f_c+2f_m))+\delta (f+(f_c+2f_m))+\delta (f-(f_c-2f_m))+\delta (f+(f_c-2f_m))]\)
\(+\frac{AJ_3(2)}{2} [\delta (f-(f_c+3f_m))+\delta (f+(f_c+3f_m))-\delta (f-(f_c-3f_m))-\delta (f+(f_c-3f_m))]\)
\(+\frac{AJ_4(2)}{2} [\delta (f-(f_c+4f_m))+\delta (f+(f_c+4f_m))+\delta (f-(f_c-4f_m))+\delta (f+(f_c-4f_m))]\)
問題5
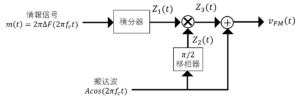
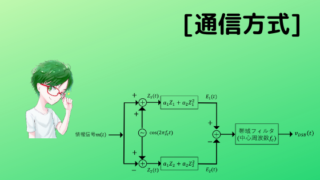
下図は狭帯域FM信号発生のアームストロング間接法を示したものである。図中の\(Z_1(t),Z_2(t),Z_3(t),v_{FM}(t)\)を導出せよ。
問題5解答
\(Z_1(t)=\int_{-\infty}^{t}2\pi \Delta F \cos(2\pi f_m t)=\frac{\cancel{2\pi} \Delta F}{\cancel{2\pi} f_m}\sin (2\pi f_m t)\)
\(\beta =\frac{\Delta F}{f_m}\)とおくと,
\(Z_1(t)=\beta \sin (2\pi f_m t)\)
<終>
\(Z_2(t)=A\cos (2\pi f_ct + \frac{\pi}{2})=A\sin (2\pi f_c t)\)
<終>
\(Z_3(t)=Z_1(t)×Z_2(t)=-A\sin (2\pi f_c t) \beta \sin (2\pi f_m t)\)
<終>
\(v_{FM}(t)= A\cos (2\pi f_ct)+ Z_3(t)\)
\(v_{FM}(t)= A[\cos (2\pi f_ct)- \sin (2\pi f_c t) \beta \sin (2\pi f_m t)]\)
\(\beta ≪1\)のとき,
\(1≒\cos [\beta \sin (2\pi f_m)],\beta \sin (2\pi f_m t) =\sin [\beta \sin (2\pi f_m t)]\)
が成立するので,\(v_{FM}\)は,
\(v_{FM}(t)≒ A[\cos (2\pi f_ct) \cos [\beta \sin (2\pi f_m)]+ \sin (2\pi f_c t) \sin [\beta \sin (2\pi f_m t)]]\)
\(v_{FM}≒A\cos [(2\pi f_c)+ \beta \sin (2\pi f_m t)]\)
問題6
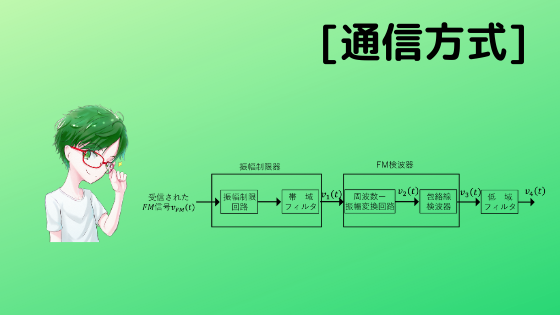
下図は,FM受信機の構成を示すブロック図である。この受信機について以下の問に答えよ。
(1) 振幅制限器はなぜ必要か。その理由を答えよ。
(2) \(v_{1}(t),v_{2}(t),v_{3}(t),v_{4}(t)\)を導出せよ。

問題6解答
(1)解答
通信路で受けた雑音やフェージングによる包絡線変動を除去するため。
(2)解答
\(v_1(t)=A \cos [2\pi f_c t+K_f\int_{-\infty}^{t}m(t)dt]\)
<終>
周波数―振幅変換回路は微分器の動作をするので,\(v_2(t)\)は,
\(v_2(t)=k \frac{d}{dt}v_1(t)\)
\(v_2(t)=kA\frac{d}{dt}\cos [\underbrace{2\pi f_c t+K_f\int_{-\infty}^{t}m(t)dt}_{x}]\)
\(v_2(t)=kA\frac{dx}{dt}\frac{d}{dx}\cos x\)
\(v_2(t)=-kA[2\pi f_c t+K_f m(t)]\sin x\)
<終>
\(v_3(t)=kA[2\pi f_c t+K_f m(t)] \)
<終>
\(v_4(t)= kA K_f m(t)\)
最後に
FM信号は計算が多くて難しいです。特に,第1種ベッセル関数が出てくるところは,計算していて死にそうになりました。