どうも,ユキです。
数々の学生を食い物にしてきた電子物性。
そんな電子物性を討伐すべく電子物性討伐隊を結成し,問題を一網打尽に攻略している。(大ウソ)
今日は,電子物性攻略法を特別に皆さんに教えましょう。
電子物性問題1
原子番号7のNと14のSiの基底状態における電子配置を示せ。
電子物性問題1解答
N:\((1s)^2(2s)^2(2p)^3\),
Si:\((1s)^2(2s)^2(2p)^6(3s)^2(3p)^2\)
電子物性問題2
炭素は原子番号6の元素であり,6つの電子を持っている。区別をつけるために,ここではそれぞれお電子1,電子2,\(\cdots\),電子6と表記する。電子の状態は4つの量子化数により量子化されており,そのうちの1つが主量子数\(n\)である。残りの3つの量子化数は何か?下の表の(a)~(c)に解答せよ。また,炭素が持つ6つの電子の基底状態における各量子数の数値を下の表に示せ。(太枠部分を解答せよ)
| 主量子数\(n\) | (a) | (b) | (c) | |
| 電子1 | ||||
| 電子2 | ||||
| 電子3 | ||||
| 電子4 | ||||
| 電子5 | ||||
| 電子6 |
電子物性問題2解答
| 主量子数\(n\) | (a) 方位量子数\(l\) | (b) 磁気量子数\(m\) | (c)スピン量子数\(m_s\) | |
| 電子1 | 1 | 0 | 0 | \(\frac{1}{2}\) |
| 電子2 | 1 | 0 | 0 | \(-\frac{1}{2}\) |
| 電子3 | 2 | 0 | 0 | \(\frac{1}{2}\) |
| 電子4 | 2 | 0 | 0 | \(-\frac{1}{2}\) |
| 電子5 | 2 | 1 | -1 | \(\frac{1}{2}\) |
| 電子6 | 2 | 1 | 0 | \(\frac{1}{2}\) |
※主量子数は,原子核からの距離
※\(s軌道(l=0),p軌道(l=1),d軌道(l=2)\)
※\(|m| \leq l\)
電子物性問題3
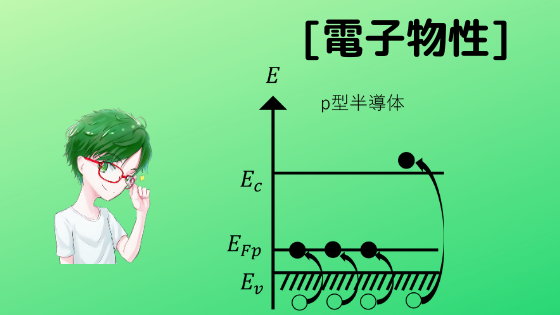
「フェルミレベル」と「バンド構造」をキーワードに用いて,導体(金属)と半導体の違いを説明せよ。
電子物性問題3解答
導体のバンド構造はフェルミレベルが伝導帯に存在するため,原子核にトラップされた電子でも自由に動き回れるが,半導体のバンド構造はフェルミレベルが価電子帯と伝導帯の間にあるので,原子核にトラップされた電子は自由に動き回れない。
電子物性問題4
陽子の周りを反転する電子(水素原子モデル)において,ボーアの仮説を適用し,主量子数\(n\)で離散化された電子の(a)軌道半径\(r\),(b)運動エネルギー\(K\),(c)全エネルギー\(E\)を求めよ。
電子物性問題4解答
電子の遠心力とクーロン力の釣り合いより,
\(m\frac{v^2}{r}=\frac{e^2}{4\pi \varepsilon_0 r^2}\)
\((mvr)^2=\frac{m e^2}{4\pi \varepsilon_0}r\)
ボーアの量子仮説\((mvr=n \hbar)\)より,
\( n^2 \hbar^2=\frac{m e^2}{4\pi \varepsilon_0}r \)
よって,軌道半径\(r\)は,
\(r=\frac{4\pi \varepsilon_0 \hbar^2}{me^2}n^2\)
運動エネルギー\(K\)について,
\(K=\frac{1}{2}mv^2=\frac{1}{2m}(mv)^2\)
\(K=\frac{1}{2m}(\frac{n \hbar}{r})^2=\frac{1}{2m}(\frac{m e^2}{4\pi \varepsilon_0 n \hbar})^2\)
\(K=\frac{1}{2m}(\frac{m e^2}{2\varepsilon_0 n h})^2=\frac{m e^4}{8\varepsilon_0^2 h^2}・\frac{1}{n^2}\)[J]
\(E=K+U=\frac{1}{2}mv^2-\frac{e^2}{4\pi \varepsilon_0 r}\)
\(E=\frac{1}{2}mv^2-mv^2=-\frac{1}{2}mv^2=-K\)[J]
\(E=-\frac{m e^4}{8\varepsilon_0^2 h^2}・\frac{1}{n^2}\)[J]
電子物性問題5
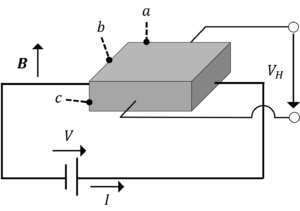
直方体状の半導体を用いて,右図のような回路を組み,ホール起電力を測定した。半導体の寸法や各電流・電流値は以下の通りである。
\(a=1cm,b=0.5cm,c=100μm,V=1.5V,\)
\(I=12mA,V_H=3mV,B=0.1T\)
(1) この半導体はn型か?p型か?理由とともに解答せよ。
(2) この半導体のキャリア密度,導電率,移動度を求めよ。
電子物性問題5解答
n型半導体。
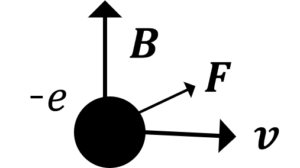
電子が受けるローレンツ力

ホールが受けるローレンツ力
ホール,電子ともに奥向きにローレンツ力を受けて,奥向きに移動する。
ホールの場合は奥向きに正の電位差が生じ,電子の場合は手前向きに正の電位差が生じる。
問題5の図において,手前向きに正の電位差が生じているので,半導体内の多数キャリアが電子であることがわかる。
キャリア密度\(n\)について,
\(n_n=\frac{I}{evS}=\frac{I}{evbc}\tag{1}\)
また,電子の速度\(v\)について,
\(v=\frac{V_H}{B b}\tag{2}\)
式(1)に式(2)を代入すると,キャリア密度\(n\)は,
\(n=\frac{bBI}{eV_H bc}=\frac{BI}{eV_Hc}\)
\(n=\frac{0.1×12×10^{-3}}{1.6×10^{-19}・3×10^{-3}・10^{-4}}=2.5×10^{22}\)[m^-3]
導電率\(\sigma \)について,
\(\sigma=\frac{aI}{SV}=\frac{aI}{bcV}\)
\(\sigma=\frac{1×10^{-2}×12×10^{-3}}{0.5×10^{-2}×100×10^{-6}×1.5}=160\)[S/m]
移動度\(μ\)は,
\(μ=\frac{\sigma}{en}=\frac{160}{1.6×10^{-19}・2.5×10^{22}}=0.04\)
電子物性問題6
半導体内の電子密度\(n\)やホール密度\(p\)は,伝導体下端エネルギー\(E_c\),価電子帯上端エネルギー\(E_v\)およびフェルミエネルギー\(E_F\)を用いて近似的に以下の式で表すことができる。
\(n=N_c exp(-\frac{E_c-E_F}{k_B T}),p=N_v exp(\frac{E_v-E_F}{k_B T})\)
(1) \(T=300K\)におけるSiの真性キャリア密度\(n_i(=p_i)\)を求めよ。Siの300Kにおける物性値は,
\(N_c=2.80×10^{25} m^{-3}\),\(N_v=1.04×10^{25} m^{-3}\),
バンドキャップは\(E_g=1.10 eV\)である。
(2) (1)のSiに\(1.00×10^{17}m^{-3}\)のP(リン)をドープした。この半導体の室温付近(300K)におけるホール密度\(p\)と電子密度\(n\)を求めよ。
電子物性問題6解答
(1)解答
熱平衡状態における真性キャリア密度\(n_i\)は,
\(n_i=\sqrt{pn}=\sqrt{N_CN_V}exp(-\frac{-E_g}{2k_BT})\)
\(n_i=\sqrt{2.8×1.04}×exp(-\frac{1.1×1.602×10^{-19}}{2・1.381×10^{-23}・300})\)
\(n_i=9.91×10^{15}\)[m^-3]
(2)解答
まず,電子密度\(n\)を求める。
熱平衡状態のn型半導体について,次の2式が成立する。
\(-n+N_D+p=0 \)
\(n_i^2=pn\)
この2式から\(p\)を消去し,\(n\)について解くと,
\(n^2-N_Dn-n_i^2=0\)
\(n=\frac{N_D+\sqrt{N_D^2+4・n_i^2}}{2}\)
\(N_D=1.00×10^{17},n_i=9.91×10^{15}\)より,電子密度\(n\)は,
\(n=\frac{1.00×10^{17}+\sqrt{(1.00×10^{17})^2+4・(9.91×10^{15})^2}}{2}\)
\(n=1.01×10^{17}\)[m^-3]
\(p=\frac{n_i^2}{n}=\frac{10^{32}}{1.01×10^{17}}=9.90×10^{14}\)[m^-3]
(3)解答
与えられた式を変形すると,
\(E_F=k_B T \ln (\frac{n}{N_C})+E_g\)
\(E_F\frac{1.381×10^{-23}}{1.602×10^{-19}}・300・\ln (\frac{1.01×10^{17}}{2.8×10^{25}})+1.1=0.597\)[eV]
(4)解答
\(\sqrt{2.8×10^{25}×1.04×10^{25}}×exp(-\frac{1.1×1.602×10^{-19}}{2・1.381×10^{-23}・400})\)
\(n_i=2.02×10^{18}\)[m^-3]
(5)解答
\(E_F=\frac{1.381×10^{-23}}{1.602×10^{-19}}・400・\ln(\frac{2.02×10^{18}}{2.8×10^{25}})+1.1=0.533\)eV
電子物性問題7
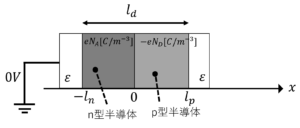
P型半導体(アクセプタ密度\(N_A\))とn型半導体(ドナー密度\(N_D\))を組み合わせて,pn接合(ダイオード)を作製した。断面積は両半導体とも\(S\)とする。
(1) 空間電荷層の厚さ(長さ)\(l_d\)を拡散電位\(V_d(=|V_D|)\)を用いて表せ。電位の基準はn型半導体側とする。
(2) ダイオードは印加電圧の周波数が高くなると整流作用を示さなくなる。その理由を説明せよ。
(3) pn接合前後の室温付近でのバンド図を示せ。バンド図では\(E_c,E_v,E_F,E_A\)(アクセプタ準位),\(E_D\)(ドナー準位)は最低限示せ。電子を●,ホールを○とし,接合面に対して左側をn型半導体とせよ。
(4) p型半導体に電圧\(V_b\)を印加する。この時,順バイアスを加えると大きな電流が流れるが,逆バイアスを加えるとわずかな電流しか流れない。その理由について,\(V_b\)を印加したときのバンド図を用いて説明せよ。
電子物性問題7解答
(1)解答
(ⅰ)\(x \leq 0\)
\(\frac{d^2 V(x)}{dx^2}=-\frac{dE(x)}{dx}=-\frac{eN_D}{\varepsilon}\)
\(E(x)= \frac{eN_D}{\varepsilon}(x+l_n)i_x (∵E(-l_n)=0)\)
\(V(x)=-\frac{eN_D}{2\varepsilon}(x+l_n)^2 (∵V(-l_n)=0)\)
(ⅱ)\(x \geq 0\)
\(\frac{d^2 V(x)}{dx^2}=-\frac{dE(x)}{dx}=-\frac{-eN_A}{\varepsilon}\)
\(E(x)= -\frac{eN_A}{\varepsilon}(x-l_p)i_x (∵E(l_p)=0)\)
\(V(x)=\frac{eN_A}{2\varepsilon}(x-l_p)^2-\frac{e}{2\varepsilon}(N_Al_p^2+N_Dl_n^2) (∵V(0)= -\frac{eN_D}{2\varepsilon}l_n^2)\)
ここで,電束密度の境界条件\(\varepsilon E(-0)・i_x=\varepsilon E(+0)・i_x\)より,
\(eN_Dl_n=-eN_A(-l_p) \)
\(N_Dl_n=N_Al_p\tag{1}\)
拡散電位\(V_d\)は,
\(V_d=|V(l_p)|=|- \frac{e}{2\varepsilon}(N_Al_p^2+N_Dl_n^2)|= \frac{e}{2\varepsilon}(N_Al_p^2+N_Dl_n^2)\tag{2}\)[V]
式(1),(2)を連立して\(l_p,l_n\)についての式を立てると,
\(V_d=\frac{e}{2\varepsilon}(N_Al_p^2+\frac{N_A^2}{N_D}l_p^2)=\frac{e N_A}{2\varepsilon N_D}(N_A+N_D)l_p^2 \)
\(V_d=\frac{e}{2\varepsilon}(N_Dl_n^2+\frac{N_D^2}{N_A}l_n^2)=\frac{e N_D}{2\varepsilon N_A}(N_A+N_D)l_n^2 \)
\(l_n,l_p\)をそれぞれ求めると,
\(l_n=\sqrt{\frac{2\varepsilon V_d}{e(N_A+N_D)}\frac{N_A}{N_D}}\)
\(l_p=\sqrt{\frac{2\varepsilon V_d}{e(N_A+N_D)}\frac{N_D}{N_A}}\)
空間電荷層の厚さ\(l_d(=l_n+l_p)\)より,求めた\(l_n,l_p\)を代入すると,
\(l_d=\sqrt{\frac{2\varepsilon V_d}{e(N_A+N_D)}}\sqrt{\frac{N_A}{N_D}}+\sqrt{\frac{N_D}{N_A}}\)
\(l_d=\sqrt{\frac{2\varepsilon V_d}{e(N_A+N_D)}}\frac{N_A+N_D}{\sqrt{N_AN_D}}\)
\(l_d=\sqrt{\frac{2\varepsilon V_d (N_A+N_D)}{e N_AN_D }}\)[m]
(2)解答
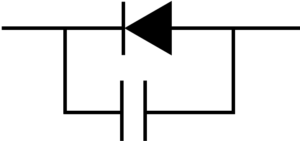
ダイオードの等価回路を書くと,
図1.ダイオードの等価回路
コンデンサを含んだ素子になる。周波数が低いときはコンデンサのインピーダンスが高いため,順方向にのみ電流は流れるが,周波数が高くなるとコンデンサのインピーダンスが低くなり,逆方向にも電流が流れてしまうから。
(3)解答
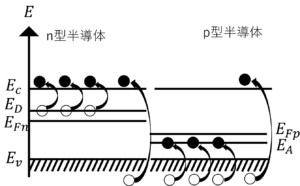
図2.pn接合前のバンド図
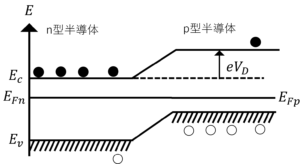
図3.pn接合後のバンド図
(4)解答
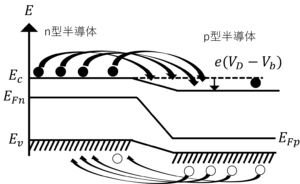
図4.p型半導体に順バイアスを加えたときのバンド図
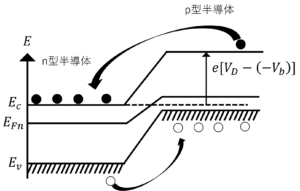
図5.p型半導体に逆バイアスを加えたときのバンド図
p型半導体に順バイアスを加えるとp型半導体内の伝導帯下端エネルギーが減少するため,多数キャリアが動き,大きな電流が流れる。一方で,p形半導体に逆バイアスを加えると,p型半導体内の伝導帯下端エネルギーが増加するため,少数キャリアしか動かず,わずかな電流しか流れない。
関連記事
通信方式R1演習問題->

通信方式H31問題->
通信方式R1演習問題->

通信方式H31問題->

最後に
電子物性は正味難しい。でも,大手企業に就職して,電子回路設計に携わっている先輩が電子物性はもう少し勉強しておけば良かったと嘆くほど重要な科目らしい。電験1種にも電子物性は選択科目として出題されることがある。(電験2種には出題されない!)要チェックや!