どうも,ユキです。
通信方式はマジで難しいですよね?
今日は,通信方式の問題の解法をシェアリングしていこうと思います。
通信方式問題1
下式で表される信号の,振幅及び位相の片側線スペクトル及び両側線スペクトルを図示せよ。
$$v(t)=1+3\cos (2\pi t+\frac{\pi}{4})+2\cos (2\sqrt{11}\pi t-\frac{\pi}{6})+\sin (12\pi t+\frac{\pi}{3})$$
通信方式問題1解答
まず,与えられた式を\(\cos \)に統一させると,
\( v(t)=1+3\cos (2\pi t・1+\frac{\pi}{4})+2\cos (2\pi t・\sqrt{11}-\frac{\pi}{6})+\cos (2\pi t・6-\frac{\pi}{6})\)
よって,片側線スペクトルは次のようになります。
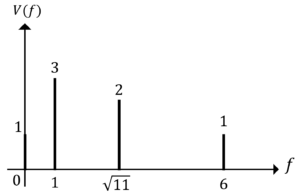
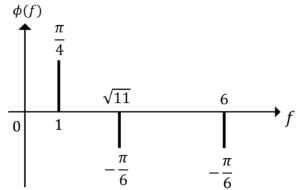
図1.片側線スペクトル
また,題意の式を
\(v(t)=1+\frac{3}{2}\cos (2\pi t・1+\frac{\pi}{4})+\cos (2\pi t・\sqrt{11}-\frac{\pi}{6})+\frac{1}{2}\cos (2\pi t・6-\frac{\pi}{6}\)
\(+\frac{3}{2}\cos -(2\pi t・1+\frac{\pi}{4})+\cos -(2\pi t・\sqrt{11}-\frac{\pi}{6})+\frac{1}{2}\cos -(2\pi t・6-\frac{\pi}{6})\)
と変形させれば,両側線スペクトルは次のように描けます。
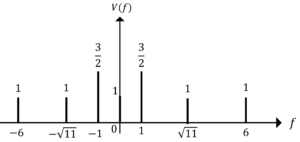
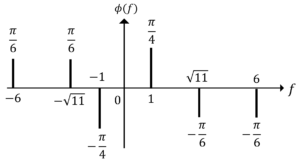
図2.片側線スペクトル
通信方式問題2
信号を複素フーリエ級数展開した場合,振幅スペクトルは偶関数,位相スペクトルは奇関数になることを証明せよ。
通信方式問題2解答
信号\(v(t)\)を複素フーリエ級数展開させると,
\(v(t)=\sum_{n=-\infty}^{\infty}|C_n|e^{jφ_n}e^{\frac{j2\pi n}{T}t}\)
※\(j\):虚数単位,\(t\):時間
振幅スペクトル\(|C_n|\)が偶関数,位相スペクトル\(φ_n\)が奇関数であることを示すためには,
\(|C_n|=|C_{-n}|\)
\(φ_{n}=-φ_{-n}\)
の2式を示せばいい。
\(|C_n|e^{jφ_n }\)について,
\(|C_n|e^{jφ_n }=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} v(t)e^{-\frac{j2\pi n}{T}t}\)
更に,\(-|C_{-n}|e^{jφ_{-n} }\)は,
\(-|C_{-n}|e^{jφ_{-n}}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} v(t)e^{-\frac{j2\pi n}{T}t}\)
となる。すると,
\(|C_n|e^{jφ_n }=-|C_{-n}|e^{jφ_{-n}}\)
であることがわかります。\( -e^{jφ_{-n}} = e^{j(-φ_{-n} )}\)を用いると,
\(|C_n| e^{j(φ_{n})}=|C_{-n}|e^{j(-φ_{-n})} \)
よって,
\(|C_n|=|C_{-n}|,φ_{n}=-φ_{-n}\)
<終>
通信方式問題3
情報信号\(m(t)\)の周波数スペクトル\(M(f)\)が右図のようになるとき,\(DSB\)信号をフーリエ変換し,その周波数スペクトルを図示せよ。

通信方式問題3解答
\(DSB\)信号\(v_{DSB}(t)\)は,搬送波周波数を\(f_c\)とすると,次式で表される。
\(v_{DSB}(t)=m(t)\cos (2\pi f_c t)\)
両辺をフーリエ変換すると,
\(V_{DSB}(f)=\int_{-\infty}^{\infty}m(t)\cos (2\pi f_c t)e^{-2\pi f t} dt\)
オイラーの公式より,
\(V_{DSB}(f)=\int_{-\infty}^{\infty}m(t)\frac{1}{2}(e^{2\pi f_c t}+ e^{-2\pi f_c t})e^{-2\pi f t} dt\)
\(V_{DSB}(f)= \frac{1}{2}(\int_{-\infty}^{\infty}m(t) e^{-2\pi (f-f_c) t} dt+\int_{-\infty}^{\infty}m(t) e^{-2\pi (f+f_c) t} dt)\)
\(V_{DSB}(f)=\frac{1}{2}(M(f-f_c)+M(f+f_c))\)
\(V_{DSB}(f)\):\(v_{DSB}(t)\)をフーリエ変換した関数
\(M(f)\):\(m(t)\)をフーリエ変換した関数
通信方式問題4
受信された\(DSB\)信号を\(v_{DSB}(t)=m(t)\cos (2\pi f_c t)\)とする。ここで,\(m(t)\)は情報信号,\(f_c\)は搬送波周波数である。
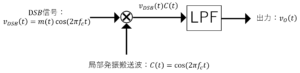
(1) \(DSB\)信号\(v_{DSB}(t)\)に局部発振搬送波\(C(t)=\cos (2\pi f_c t)\)を同期させることにより,情報信号\(m(t)\)が取り出されることを示せ。
(2) 局部発振搬送波の周波数が\(\Delta f\),位相が\(\Delta φ\)ずれた場合,どのような波形が出力されるか説明しなさい。
通信方式問題4解答
(1)解答
ブロック図を示す
出力される信号を\(v_O(t)\)とすると,
\(v_O(t)=v_{DSB}(t)C(t)\)
\(v_O(t)=m(t)\cos^2 (2\pi f_c t)\)
\(v_O(t)=m(t)\frac{1+\cos (4\pi f_c t)}{2}\)
\(LPF\)(ローパスフィルター)は低い周波数のみを通すので,
\(v_O(t)=\frac{1}{2}m(t)\)
信号\(m(t)\)の\(\frac{1}{2}\)倍の大きさの信号が得られる。
<終>
(2)解答
ブロック図を示すと,
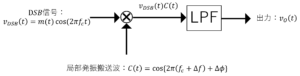
出力信号\(v_O\)は,
\(v_O(t)=v_{DSB}(t)C(t)\)
\(v_O(t)=m(t)\cos (2\pi f_c t)\cos [2\pi (f_c+\Delta f_c)t +\Delta φ]\)
\(v_O(t)=m(t)\frac{\cos [2\pi (2f_c+\Delta f_c)t +\Delta φ]+\cos (2\pi \Delta f_c t +\Delta φ)}{2}\)
\(LPF\)(ローパスフィルター)は低い周波数のみを通すので,
\(v_O(t)=\frac{1}{2}m(t) \cos (2\pi \Delta f_c t +\Delta φ) \)
元の信号\(m(t)\)に,周波数オフセット\(\Delta f_c\)と位相オフセット\(\Delta \)が加わった波形が出力される。
関連記事
通信方式H31演習問題->

電子物性H31問題->
<終>
最後に
通信方式の途中計算がわからない時は,「フーリエ解析」を復習しておけばいいと思います。通信方式の根本を理解する必要はないと思いますが,教科書の式変形を自分で追えるようにはなってください。