この記事を読むメリット
☑アンペールの周回積分の法則について理解できる
アンペールの周回積分の法則とは?
磁束密度\(B\)を計算する一般的な方法として,ビオ-サバールの法則がありました。
今回は,そんなアンペールの法則よりも簡単に磁束密度を計算できるアンペールの周回積分の法則についてご紹介します。
アンペールの周回積分の法則は,式で表すと以下の通りです。
$$\int_{c}B・ds=\mu_0 NI$$
\(\mu_0\)は真空の透磁率,\(I\)は電流,\(N\)は,積分路と電流が鎖交する回数です。
積分路と電流が鎖交するとはどういうことでしょうか?
例えば、
3回巻きのコイルであれば,積分路と電流の鎖交数が3回なので、\(N=3\)となり、
$$\oint_{c}B・ds=3\mu_0 I$$
となります。
下の図のように、積分路が電流と3回ほど鎖交したときは、\(N=3\)で、
->
$$\oint_{c}B・ds=3\mu_0 I$$
と表すことができます。
このアンペールの法則を磁束密度\(B\)について解くだけで,磁束密度\(B\)を求めることはできますが,
求めることができる磁束密度\(B\)は,対称性のあるものに限定されます。
では,早速例題を解いていきましょう。
例題1

無限長直線電流による磁束密度\(B\)をアンペールの周回積分の法則を用いて導きなさい。
例題1解答
半径\(r\)の閉ループ積分路をとると,鎖交回数\(N=1\)なので,アンペールの周回積分の法則より
\(\int_{c}B・ds=\mu_0 I\)
となります。ここで,微小ベクトル\(ds=r d \phi i_{\phi}\),磁束密度\(B=|B|i_{\phi}\)より,
\(|B|\int_{0}^{2\pi}i_{\phi}・i_{\phi}r d\phi=\mu_0 I\)
\(|B|\underbrace{\int_{0}^{2\pi}r d\phi}_{2\pi r} =\mu_0 I\)
\(|B|=\frac{\mu_0 I}{2\pi r}\)
\(B=\frac{\mu_0 I}{2\pi r}\)[T]
例題2
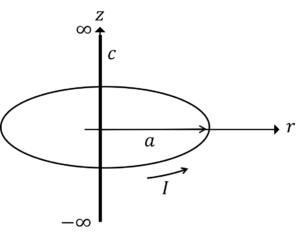
半径\(a\)の円形導線に電流\(I\)が流れているとき,円の中心軸(\(z\)軸)上で\(-\infty \to \infty\)まで磁束密度\(B\)の線積分を行うと,その値はいくらになりますか?
(1) アンペールの法則を用いて求めなさい。
(2) 直接積分を用いて求めなさい。
例題2解答
(1)解答
アンペールの法則を用いると,積分路と電流の鎖交回数\(N=1\)なので,
\(\int_{c}B・ds=\mu_0 I\)
となる。
<終>
(2)解答
半径\(a\)の円形導線に流れる電流\(I\)が点\((z,0,0)\)に作る磁束密度の大きさ\(|B|\)について考える。
ビオ-サバールの法則より,
\(|B|=\int_{c} \frac{\mu_0 I |ds(r’)|\sin \theta}{4\pi |r-r’|^2}\)
\(|ds(r’)|=a d\phi\),\(|r-r’|=\sqrt{z^2+a^2}\),\(\sin \theta=\frac{a}{\sqrt{z^2+a^2}}\)より,
\(|B|=\int_{0}^{2\pi}\frac{\mu_0 I a^2 d\phi}{4\pi (z^2+a^2)^{\frac{3}{2}}}\)
\(|B|=\frac{\mu_0 I a^2}{2(z^2+a^2)^{\frac{3}{2}}}\)
ここで,磁束密度\(B\)について,\(z:-\infty \to \infty\)の範囲で積分してあげると,
\(\int_{-\infty}^{\infty}|B|dz=\int_{-\infty}^{\infty}\frac{\mu_0 I a^2}{2(z^2+a^2)^{\frac{3}{2}}}dz\)
\(z=a \tan \theta\)とおくと,\(dz=\frac{a}{\cos^2 \theta}d\theta\),積分範囲は,\(\theta:-\frac{\pi}{2} \to \frac{\pi}{2}\)より,
\(\int_{-\infty}^{\infty}|B|dz=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\mu_0 I a^2}{2a^3(1+\tan^2 \theta)^{\frac{3}{2}}}\frac{a}{\cos^2 \theta} d\theta\)
\(\int_{-\infty}^{\infty}|B|dz=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\mu_0 I }{2} \cos \theta d\theta\)
\(\int_{-\infty}^{\infty}|B|dz=[\frac{\mu_0 I }{2} \sin \theta]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\)
\(\int_{-\infty}^{\infty}|B|dz=\mu_0 I\)
アンペールの法則|まとめ
アンペールの法則は,対称性のある磁束密度\(B\)を計算するときに用いられ,
$$\int_{c}B・ds=\mu_0 I$$
で表される。
最後に
物理学において,対称性というフレーズは結構便利だったりします。
例えば,今日の記事で紹介した対称性のある磁束密度や磁界は,アンペールの法則を使えば求められます。
同様に,対称性のある電界や電束密度に関しては,ガウスの法則を使えば求められます。
対称性を使えば,難しい積分を解かずに済むケースが出てきます。