この記事を読むメリット
☑ビオ-サバールの法則を使って磁束密度を計算できるようになる
磁束密度とは?
磁束\(\Phi\)とは,面\(S\)を出て行く磁束線の本数を表します。磁束\(Phi\)の単位は,ウェーバー(Wb)です。
磁束密度を\(B\)とすると,磁束\(\Phi\)は,
$$\Phi=\int_{S}B・ndS$$
となります。磁束線は,電気力線に対応して名付けられたものです。
電気力線に関する記事->

磁束\(\Phi\)に対して,磁束密度\(B\)の単位は,テスラ(T)または,(Wb/m^2)で表されます。
しかし,どうして磁束線の本数\(\Phi\)は,ベクトル面積分を使うのでしょうか?
高校物理の教科書には,
$$\Phi=BS$$
と表されています。確かに,面\(S\)で一様な磁束密度\(B\)であれば,この式でも大丈夫なのですが,
磁束密度\(B\)が,面\(S\)を通過している事を確かめる為には,単位ベクトル\(n\)との内積を調べなければいけません。
つまり,
$$B・n$$
磁束密度\(B\)の\(n\)に垂直な成分は,面\(S\)を通過せず,\(n\)に平行な成分のみ,磁束線の本数として,カウントしてあげます。
そして,面\(S\)全体を積分してあげれば,磁束\(\Phi\)が求まります。
$$\Phi=BS$$
ビオ-サバールの法則は磁束密度を求める法則!!
続いて,ビオ-サバールの法則に関するお話をします。
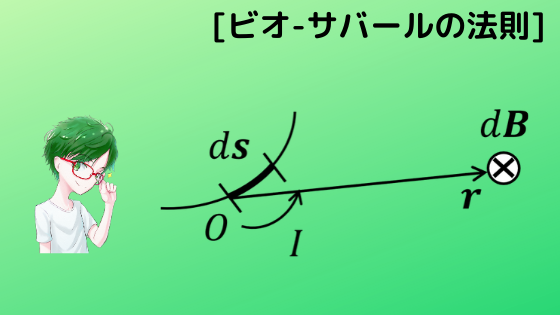
微小な磁束密度\(dB\)とし,ビオ-サバールの法則を使うと,
$$dB=\frac{μ_0Ids×r}{4\pi |r|^3}$$
となります。\(μ_0\)は,真空の透磁率,\(r\)は位置ベクトル,\(I\)は電流,\(ds\):微小長さのベクトルです。
図で表すとこんな感じです。
これを使えば,電流が作る磁束密度を自由自在に求めることができるようになります。
ただし,この式だと不十分なので,ビオ-サバールの法則を拡張します。
$$dB=\frac{μ_0Ids(r’)×(r-r’)}{4\pi |r-r’|^3}$$
よって,磁束密度\(B\)は,
$$B=\int_c \frac{μ_0Ids(r’)×(r-r’)}{4\pi |r-r’|^3}$$
とすれば,任意電流が作る磁束密度を求めることができます。
磁束密度に関する例題1
(1) \(2l\)[m]の直線導線に流れる電流が点Pに作る磁束密度\(B\)を求めなさい。
(2) \(l \to \infty\)としたときの磁束密度\(B\)を求めなさい。
例題1解答
(1)解答
微小長さ\(ds\)の導線を流れる電流\(I\)による点Pの磁束密度は,\(dB\)であるから,ビオ-サバールの法則より,
\(dB=\frac{μ_0Ids(r’)×(r-r’)}{4\pi |r-r’|^3}\)
ここで,\(r=|r|i_r\),\(r’=|z|i_z\),\(ds(r’)=|z|i_r\)としてあげれば,
\(dB=\frac{μ_0Id|z|i_z×(|r|i_r-|z|i_z)}{4\pi ||r|i_r-|z|i_z|^3}\)
\(dB=\frac{μ_0I|r|}{4\pi (|r|^2+|z|^2)^{\frac{3}{2}}}d|z| i_{\phi}\)
導線全体を流れる電流\(I\)による磁束密度\(B\)は,
\(B=\int_c\frac{μ_0I|r|}{4\pi (|r|^2+|z|^2)^{\frac{3}{2}}}d|z| i_{\phi}\)
\(B=\int_{-l}^{l} \frac{μ_0I|r|}{4\pi (|r|^2+|z|^2)^{\frac{3}{2}}}d|z| i_{\phi}\)
\(|z|=|r|\tan \theta\)とおくと,\(\frac{d|z|}{d\theta}=\frac{|r|}{\cos^2 \theta}\)となり,
積分範囲は,\(\theta:\theta_1 \to \theta_2\)になります。

\(B=\int_{\theta_1}^{\theta_2}\frac{μ_0I|r|}{4\pi |r|^3(1+\tan^2 \theta)^{\frac{3}{2}}}\frac{|r|}{\cos^2 \theta} d\theta i_{\phi}\)
\(1+\tan^2 \theta=\frac{1}{\cos^2 \theta}\)より,
\(B=\int_{\theta_1}^{\theta_2}\frac{μ_0I \cos \theta}{4\pi |r|} d\theta i_{\phi}\)
\(B=[\frac{μ_0I \sin \theta}{4\pi |r|}]_{\theta_1}^{\theta_2} i_{\phi}\)
\(B=[\frac{μ_0I}{4\pi |r|}[\sin \theta_2-\sin \theta_1] i_{\phi}\)
\(\sin \theta_2=\frac{l}{\sqrt{|r|^2+l^2}}=-\sin \theta_1\)より,
\(B=\frac{μ_0 I}{2\pi |r|}\frac{l}{\sqrt{|r|^2+l^2}} i_{\phi}\)[T]
<終>
(2)解答
\(B=\displaystyle \lim_{l \to \infty} \frac{μ_0 I}{2\pi |r|}\frac{l}{\sqrt{|r|^2+l^2}} i_{\phi}\)
\(B=\displaystyle \lim_{l \to \infty} \frac{μ_0 I}{2\pi |r|}\frac{1}{\sqrt{(\frac{|r|}{l})^2+1}} i_{\phi}\)
\(B=\frac{μ_0 I}{2\pi |r|} i_{\phi}\)[T]
円形導線が作る磁束密度
続いて,円形導線に流れる電流が作る磁束密度を求めていきましょう。この結果は,ソレノイドの内部磁界を計算するときに使われます。
では,ビオ-サバールの法則を使って,求めて行きましょう。
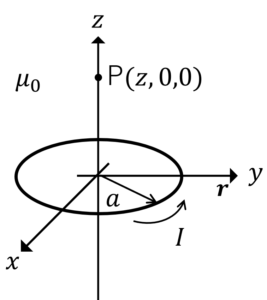
例題2
半径\(a\)の円形導線に電流\(I\)が流れています。点Pにおける磁束密度を求めましょう。
例題2解答
微小長さ\(ds\)の導線を流れる電流\(I\)が作る磁束密度は,\(dB\)なので,
ビオ-サバールの法則より,微小な磁束密度\(dB\)は,
\(dB=\frac{μ_0Ids(r’)×(r- r’)}{4\pi |r- r’|^{3}}\)
ここで,\(B=B_ri_r+B_zi_z\)とすると,磁束密度の対称性から\(B_r=0\)となるので,
\(B=B_zi_z\)
となる。これを踏まえてビオ-サバールの法則を書き直すと,
\(dB_z=\frac{μ_0I|ds(r’)|\sin \theta}{4\pi |r-r’|^2}\)
\(ds(r’)=ad\phi i_{\phi}\),\(|r-r’|=\sqrt{r^2+a^2}\),\(\sin \theta=\frac{a}{\sqrt{r^2+a^2}}\)
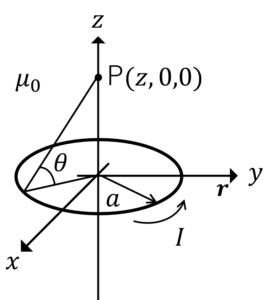
\(dB_z=\frac{μ_0I a^2 d\phi\}{4\pi (r^2+a^2)^{\frac{3}{2}}i_{\phi}\)
\(B_z=\int_{0}^{2\pi}\frac{μ_0I a^2 d\phi\}{4\pi (r^2+a^2)^{\frac{3}{2}}\)
\(B=\frac{μ_0I a^2}{2(r^2+a^2)^\frac{3}{2}}i_z\)[T]
ベクトルポテンシャルに関するビオ-サバールの法則
ビオ-サバールの法則は,ベクトルポテンシャル\(A\)を使うと少し簡単に書けることが知られています。
$$dA=\frac{μ_0 I ds(r’)}{4\pi |r- r’|}$$
こんな式で書けます。
ベクトルポテンシャルは,磁束密度\(B\)を使って次のように定義されています。
$$B=∇×A$$
ベクトルポテンシャル\(A\)の単位は,([Wb/m]または[T・m])です。これは,∇(ナブラ)の単位が(1/m)であることを知っていると導出可能です。
ベクトルポテンシャルは,電験で1回だけ出題されました。
誘導付きの問題なので,是非力試しで解いてみてください。
ビオ-サバールの法則|まとめ
磁束\(\Phi\)は,磁束線の本数である。
$$\Phi=\int_{S}B・n dS$$
ビオ-サバールの法則は,一般的に
$$dB=\frac{μ_0 Ids(r’)×(r- r’)}{4\pi |r- r’|^3}$$
と表される。この式の両辺に大きさをとれば,
$$d|B|=\frac{μ_0 I d|s(r’)| \sin \theta)}{4\pi |r- r’|^2}$$
となる。
また,ベクトルポテンシャル\(A\)に関するビオ-サバールの法則は,
$$ dA=\frac{μ_0 I ds(r’)}{4\pi |r- r’|}$$
となる。
最後に
ビオ-サバールの法則は,磁束密度を求める為のツールとして知られています。コイルの磁束密度を求めるときに役立ちますが,計算が面倒くさいです。ぴえん。
アンペールの法則を使えば,簡単に計算できるもん!