どうも,ユキです。今日も,FXに関する記事です。移動平均線っていくつも種類があるじゃないですか?
まあ,結論を言うと,単純移動平均を使えばいいよ!と思いますが,一体なぜ?移動平均線とその種類について考えていきましょう。
この記事を読むメリット
☑移動平均線が先を予測する力がないことが分かる
☑移動平気線には傾向を掴む力があることが分かる
☑いちばん良い移動平均線がわかる
移動平均線
移動平均線とは,ある一定期間の終値(おわりね)の平均値を線で結んだものです
例えば,移動平均線には,5日線,10日線などがあり,
5日線(5日移動平均線)なら5日の終値の平均値,10日線(10日移動平均線)なら10日の終値の平均値を線で結んでいます。
そして,そんな移動平均線には様々な種類があります。
平均に関する記事と重複する箇所があります。

ここまで読んだあなたは,いちばん良い移動平均線があるのではないか?先を読みやすい移動平均線はないのか?と考えるでしょう。
最初に断言しますが,そんな都合のいい移動平均線は存在しませんw
理由は,移動平均線の種類を紹介した後で説明します。
それでは,どんな移動平均線があるのかを見ていきましょう。
本日ご紹介する移動平均線は全部で5つです。
・単純移動平均
・加重移動平均
・指数移動平均
->・修正移動平均
・正弦加重移動平均
三角移動平均は,数式表現にmodとか出てくるので,紹介しません。
単純移動平均
単純移動平均は,皆さんがよく用いている相加平均と同じです。
そして,移動平均線は,直近\(N\)日間の終値(おわりね)の平均なので,式表現は,
単純移動平均を\(SMA\)(Simple Moving Average),終値を\(p_{t-i} i∈(1,2,3,\cdots,N)\)とすると,
$$SMA_t=\frac{1}{N}\sum_{i=1}^{N}p_{t-N+i}$$
と書けます。(\(\sum\)で書いていますが,未成年者に読まれるとまずい記事なので,)
そして,昨日(\(t-1\)日)の単純移動平均\(SMA_{t-1}\)から,今日(\(t\)日)の単純移動平均\(SMA_t\)を求めたい場合は,
$$SMA_{t}=SMA_{t-1}+\underbrace{\frac{p_M-N}{N}}_{古い終値}+\underbrace{\frac{p_t}{N}}_{新しい終値}$$
として求めます。つまり,今日の\(SMA\)を求める為には,新しい終値を加え,古い終値を引けばいいと言うことがわかります。
単純移動平均線のデータの重みを見てみるとこんな感じになっています。
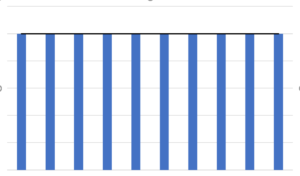
単純移動平均線は,長期のトレンドを見るのには向いていますが,
平均的な価格から大きく外れた価格が出ると,その影響を受けすぎるのが欠点です。
例えば,5日線で,100円,100円,100円,100円となっている相場にいきなり150円が現れると,
単純移動平均\(SMA\)は,
\(SMA=\frac{1}{5}[150+100+100+100+100]=110円\)
となります。更に,150円が出続けると,
\(SMA=\frac{1}{5}[150+150+100+100+100]=120円\)
\(SMA=\frac{1}{5}[150+150+150+100+100]=130円\)
\(SMA=\frac{1}{5}[150+150+150+150+100]=140円\)
\(SMA=\frac{1}{5}[150+150+150+150+150]=150円\)
となり,新たな相場の平均線を描くのに\(N\)日かかってしまいます。
要は,単純移動平均線\(SMA\)は,相場の転換に素早く対応できないということです。
これに対処するために作られたのが,加重移動平均\(WMA\)と指数移動平均\(EMA\)で,加重移動平均,指数移動平均を使うと,相場の転換に素早く対応できます。
・単純移動平均のデメリット
1.\(N\)日分の値動きしか考慮されていない
2.各期間内のデータの重みが全て同じ(平均から離れた値に影響を受けやすい)
加重移動平均
単純移動平均をパワーアップさせたい。
そこで,加重移動平均の出番です。
加重移動平均は,加重平均のことを言います。物理学でよく出てきます。
加重移動平均\(WMA\)(Weighted Moving Average)の式は,終値\(P_{t-i} \)を用いると
$$WMA_t=\frac{\sum_{i=1}^{N}i・p_{t-N+i}}{\sum_{i=1}^{N}i}$$
となります。(物体の重心を求める公式と同じです。)
そして,昨日の加重移動平均\(WMA_{t-1}\)から,今日の加重移動平均\(WMA_{t}\)を計算するには,
$$WMA_t=WMA_{t-1}+\frac{\sum_{i=0}^{N-1}p_t-p_{t-N+i}}{\sum_{i=1}^{N}i}$$
加重移動平均\(WMA\)の重みをグラフに表すと,
加重移動平均は,単純移動平均と比べて強化された所は,
このように,過去の相場の大変動に影響されにくい形になっている所です。
指数移動平均も,過去の相場の大変動に影響されにくい形の1つですが,加重移動平均とは重みが違います。
指数移動平均
加重移動平均は,単純移動平均線のデメリットを1つ解消しました。
指数移動平均\(EMA\)(Exponential Moving Average)は,単純移動平均線のデメリットを2つとも解消できることができます。
昨日の指数移動平均\(EMA_{t-1}\)から,今日の指数移動平均を求めてみますと,
$$EMA_{t}=\underbrace{\alpha}_{\frac{2}{N+1}} \times p_{t}+(1-\underbrace{\alpha\frac{2}{N+1}})\times EMA_{t-1}$$
となります。気づいた方がいらっしゃるかも知れませんが,
指数移動平均\(EMA\)を計算する為に,無限個の終値(おわりね)を必要とします。
指数移動平均\(EMA_t\)を展開し,\(\alpha=\frac{2}{N+1}\)とおくと,
$$EMA_t=\alpha \sum_{i=0}^{\infty}(1-\alpha)^{i} p_{t-i}$$
で表されます。
指数移動平均線のデータの重みはこんな感じです。
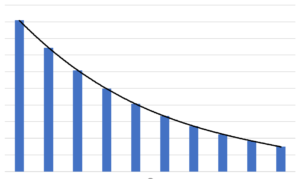
余談ですが,指数移動平均を加重移動平均風に表すと,
$$EMA_t=\frac{\sum_{i=0}^{N}(1-\alpha)^{i}}{\sum_{i=0}^{\infty}(1-\alpha)^i}$$
となります。
指数移動平均は,単純移動平均を古い価格の影響を受けないように加工したものになります。
指数移動平均を使うと,単純移動平均よりも相場の変化に気づきやすいですが,長期のトレンドを調べるのには向きません。(トレードオフです。)
修正移動平均
しかし,指数移動平均だと,値動きに対する反応が良すぎて,ダマシにひっかかりやすくなります。
そこで,修正移動平均の登場です。
修正移動平均線のデータの重みは、指数移動平均線に比べて緩やかになっています。
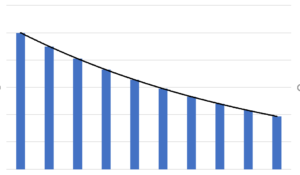
修正移動平均\(MMA\)(Modified Moving Average)は,終値\(p_{t-N+i}\),\(i=1,2,3,\cdots,N\)とすると,
$$MMA_{t}=\frac{(N-1) \times MMA_{t-1}+p_{t}}{N}$$
指数移動平均\(EMA\)は,
$$EMA_t=\frac{\sum_{i=0}^{\infty}(1-\alpha)^{i}}{\sum_{i=0}^{\infty}(1-\alpha)^i}$$
\(\alpha=\frac{2}{N+1}\)
で表されていました。
つまり,修正移動平均\(MMA\)は,指数移動平均の\(\alpha\)を\(\alpha=\frac{1}{N}\)としたものです。
修正移動平均を使うと,全てのデータを反映させつつ,単純移動平均より値動きに対する反応を速くできます。
正弦加重移動平均
結論から言うと,正弦加重移動平均は,先ほど紹介した4つに比べてあまり使えません。(三角移動平均も役立たずです)
理由を説明する前に,正弦加重移動平均\(SWMA\)(Sine Weighted Moving Average)の式を見ていきましょう。
終値を\(p_{t-N+i} i_{t-N+i} i∈(1,2,3,\cdots,N)\)とすると,正弦加重移動平均\(SWMA\)は,
$$\sum_{i=1}^{N}\frac{\sum_{i=1}^{N}p_{t-N+i}\times \sin (\pi \frac{i}{n+1}) }{\sum_{i=1}^{N} \sin (\pi \frac{i}{n+1})}$$
となります。うん。だからなんだよ!って感じですよね?
要は,直近の終値ではなく,真ん中の終値の影響が大きく出るということです。
これでは,反応性が良いとは言えませんね!(真ん中の終値に大きく依存してしまうから。)
また,傾向を掴む点においても,単純移動平均線に劣ってしまいます。
更に,無駄に計算が難しいです!(三角移動平均も計算が面倒くさい)
数学マスターであるこの私も分析できません。(トホホ……。)
移動平均線比較
復習をしましょう。今,単純移動平均線,加重移動平均線,指数移動平均線,修正移動平均線について学習しました。
結論から言うと,どの移動平均線も一長一短で,一概にどの移動平均線が優れているとは言えないです。
その理由は,2つあります。
1.値動きは8.5割がランダムウォークだから。
2.移動平均線はあくまで,傾向を掴むものであって,未来を予測できるものではないから。
一つ目の理由にもあるとおり,値動きはランダムに動きます。
ここで勘違いして欲しくないのは,値段が1/2の確率で値上がりし,1/2の確率で値下がりするわけ(対称ランダムウォーク)ではないということです。
具体例を挙げるとするなら,高金利通貨で有名なトルコリラ,メキシコペソ,南アフリカランドの値動きを見れば一目瞭然(いちもくりょうぜん)です。
移動平均線は,未来を予測することはできませんが,このような通貨の非対称性を見抜くことに使えます。
それでは,移動平均線の性能を比較します。
表にしてまとめると,
| 単純移動平均線 | 加重移動平均線 | 指数移動平均線 | 修正移動平均線 | |
| 精度 | 超高 | 低 | 超低 | 中 |
| 即効性 | 超低 | 高 | 超高 | 中 |
こんな感じになります。
パレート最適(あちらをたてればこちらがたたず)な移動平均線は以上の4つになります。
最後に
ここまで読んでくださってありがとうございます。感謝してもしきれない思いでいっぱいですが,最後に残念なお知らせがあります。
実は,皆さん私の誘導にのせられています。(ドヤァ)
先ほど,4つの移動平均線を比較しましたが,実は,ここには行動経済学のテクニックを使っています。そう,誘導通りならば貴方は,修正移動平均線を使うでしょう!
どういうことか?
というと,これは行動経済学の極端回避性を用いています。
おっと,余計なことを口走ってしまいました。それでは,この辺でさようなら。