[通信方式]DSB･AM信号の変調方法に関する演習問題

$$\require{\cancel}$$

ユキ

金持ちになりたい。どうも，ユキです。

皆さんはお金を稼いだ後，その稼いだお金をどうしますか？

私は自己投資にまわします。

そんな話はどうでもいいので，今日も通信方式の問題を解いていこうと思います。

問題1

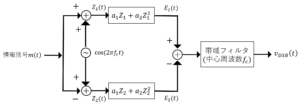
下図は，DSB信号発生用の平衡変調器を示したものである。下図中の$Z_1(t)，Z_2(t)，E_1(t)，E_2(t)，V_{DSB}(t)$を導出せよ。

平衡変調器

問題1解答

$Z_1(t)=m(t)+\cos (2\pi f_c t)$

$Z_2(t)= -m(t)+\cos (2\pi f_c t)$

$E_1(t)= a_1(m(t)+\cos (2\pi f_c t))+a_2( m(t)+\cos (2\pi f_c t))^2$

$E_2(t)=a_1(-m(t)+\cos (2\pi f_c t))+a_2(-m(t)+\cos (2\pi f_c t))^2$

$ E_1(t)-E_2(t)= a_1( m(t)+\cos (2\pi f_c t))+a_2( m(t)+\cos (2\pi f_c t))^2$

$-[ a_1(-m(t)+\cos (2\pi f_c t))+a_2(-m(t)+\cos (2\pi f_c t))^2]$

$E_1(t)-E_2(t)=2a_1m(t)+a_2( \cancel{m(t)}+\cos (2\pi f_c t)- \cancel{m(t)}$

$+\cos (2\pi f_c t))( m(t)+\cancel{\cos (2\pi f_c t)}-(-m(t)+\cancel{\cos (2\pi f_c t)}))$

$ E_1(t)-E_2(t)= 2a_1m(t)+4a_2m(t)\cos (2\pi f_c t)$

$ E_1(t)-E_2(t)$を帯域フィルタ(中心周波数$f_c$)に通すと，出力信号$v_{DSB}(t)$が得られる。よって，$v_{DSB}(t)$は，

$v_{DSB}(t)= 4a_2m(t)\cos (2\pi f_c t)$

問題2

受信されたDSB信号を$V_{DSB}(t)=m(t)\cos (2\pi f_ct)$とする。ここで，$m(t)$は情報信号，$f_c$は搬送波周波数である。DSB信号$v_{DSB}(t)$に局部発振搬送波$C(t)=\cos (2\pi f_c t)$を同期させることにより，情報信号$m(t)$が取り出されることを示せ。

問題2解答

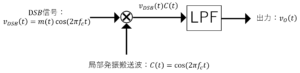
$v_{DSB}(t)$に局部発振搬送波$C(t)$を同期させる様子を以下のブロック図に示す。

$V_{DSB}(t)C(t)= m(t)\cos (2\pi f_ct) \cos (2\pi f_ct)$

$V_{DSB}(t)C(t)= m(t)\frac{1+\cos (4\pi f_ct)}{2}$

$V_{DSB}(t)C(t)$をローパスフィルタに通すと，出力信号$v_O(t)$が得られる。よって，$v_O(t)$は，

$v_O(t)=\frac{1}{2}m(t)$

情報信号を1/2倍した波形が取り出される。

問題3

DSB信号$V_{DSB}(t)=m(t)\cos (2\pi f_ct)$と通常の振幅変調$v_{AM}(t)=A\cos (2\pi f_c t)+v_{DSB}(t)$の周波数スペクトルを導出し，その違いを説明せよ。ここで$m(t)$は変調信号，$f_c$は搬送波周波数である。

問題3解答

$v_{DSB}(t)，v_{AM}(t)$をフーリエ変換した関数をそれぞれ$V_{DSB}(f)，V_{AM}(f)$とすると，

$V_{DSB}(f)=\int_{-\infty}^{\infty} m(t)\cos (2\pi f_ct)exp(-j2\pi ft)dt$

$V_{DSB}(f)=\int_{-\infty}^{\infty} m(t)\frac{ exp(j2\pi f_ct)+ exp(-j2\pi f_ct)}{2} exp(-j2\pi ft)dt $

$V_{DSB}(f)=\frac{1}{2}\int_{-\infty}^{\infty} m(t) exp(-j2\pi (f-f_c)t)dt+\frac{1}{2}\int_{-\infty}^{\infty} m(t) exp(-j2\pi (f+f_c)t)dt $

$V_{DSB}(f)=\frac{1}{2}(M(f-f_c)+M(f+f_c))$

<終>

$v_{AM}(t)= A\cos (2\pi f_c t)+ m(t)\cos (2\pi f_ct)$

$v_{AM}(t)=[A+m(t)]\cos (2\pi f_ct)$

両辺をフーリエ変換すると，

$v_{AM}(f)= \frac{1}{2}\int_{-\infty}^{\infty} [A+m(t)] exp(-j2\pi (f-f_c)t)dt$

$+\frac{1}{2}\int_{-\infty}^{\infty} [A+m(t)] exp(-j2\pi (f+f_c)t)dt $

$V_{AM}(f)=\frac{1}{2}(M(f-f_c)+M(f+f_c))+\frac{A}{2}(\delta (f-f_c)+\delta(f+f_c))$

AM信号は、DSB信号にインパルスを追加したものである。

問題4

下図は，通常のAM信号発生用の2乗素子変調器を示したものである。下図中の$Z_1(t)，Z_2(t)，v_{AM}(t)$を導出せよ。

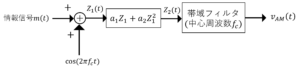
問題4解答

$Z_1(t)=m(t)+A\cos (2\pi f_c t)$

$Z_2(t)=a_1(m(t)+A\cos (2\pi f_c ))+a_2(m(t)+A\cos (2\pi f_c ))^2$

$Z_2$を中心周波数$f_c$の帯域フィルタを通すと，$v_{AM}(t)$が得られる。

よって，$v_{AM}(t)$は，

$v_{AM}(t)=A[a_1+2a_2m(t)]\cos (2\pi f_c t)$

問題5

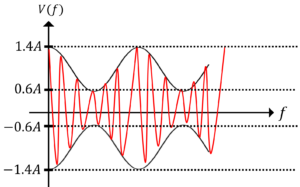
AM信号を$v_{AM}(t)=A(1+m_0(t))\cos (2\pi f_c t)$とする。変調信号がトーン信号$m_0(t)=\cos (2\pi f_m t)$の場合，変調率が0.4のときの$v_{AM}(t)$波形を図示せよ。

問題5解答

問題6

DSB信号を$v_{DSB}(t)=Am\cos (2\pi f_m t)\cos (2\pi f_c t)$，AM信号を$v_{AM}(t)=v_{DSB}(t)+A\cos (2\pi f_c t)$とする。このときDSB信号およびAM信号の伝送効率（＝側波帯電力/全電力）を求めよ。ただし信号の電力は以下のように定義する。

$$P=\frac{1}{T}\int_{0}^{T}v^2(t)dt$$

問題6解答

DSB信号の伝送効率とAM信号の伝送効率をそれぞれ$η_{DSB}，η_{AM}$とすると，

$η_{DSB}=\frac{ \frac{1}{T}\int_{0}^{T}v_{DSB}(t)^2dt }{ \frac{1}{T}\int_{0}^{T}v_{DSB}(t)^2dt }=1$

$η_{AM}=\frac{ \frac{1}{T}\int_{0}^{T}v_{DSB}(t)^2 dt }{\frac{1}{T}\int_{0}^{T}A\cos (2\pi f_c t)^2 dt +\frac{1}{T}\int_{0}^{T}v_{DSB}(t)^2dt }$

$η_{AM}=\frac{ \frac{1}{T}\int_{0}^{T}A^2m^2(\frac{\cos (2\pi (f_c+f_m)t)+\cos (2\pi (f_c-f_m)t)}{2})^2 dt }{\frac{1}{T}\int_{0}^{T}A^2 \cos (2\pi f_c t)^2dt +\frac{1}{T}\int_{0}^{T}A^2m^2(\frac{\cos (2\pi (f_c+f_m)t)+\cos (2\pi (f_c-f_m)t)}{2})^2 dt }$

$η_{AM}=\frac{ \frac{A^2m^2 }{4}}{\frac{A^2}{2}+\frac{A^2m^2 }{4}}$

$η_{AM}=\frac{m^2}{2+m^2}$

問題7

0.3kHz～3.4kHzに帯域制限された情報信号$m(t)$を10MHzの搬送波でSSB信号を作るとき，1段フィルタ法と2段フィルタ法による間隙帯域幅（両側波帯間の隙間）をそれぞれ求めよ。ただし，2段フィルタ法での第1フィルタにおける搬送波を100kHzとする。

問題7解答

1段フィルタ法で生じる間隙帯域幅$\Delta f_1$は，

$\Delta f_1=2×(10000+0.3)=20000.6$[kHz]

2段フィルタ法で生じる間隙帯域幅$\Delta f_2$は，

$\Delta f_2=2×(100+\frac{\Delta f_1}{2})=20200.6$[kHz]

問題8

「$SSB$信号は$DSB$信号に直交成分を加えたものである」
このことをトーン信号$m_0(t)=\cos (2\pi f_m t)$を持つ$DSB$信号$v_{DSB}(t)=m_0(t)\cos (2\pi f_c t)$を用いて説明しなさい。

問題8解答

$v_{DSB}(t)=\cos (2\pi f_m t) \cos (2\pi f_c t)$

$v_{DSB}(t)=\underbrace{\frac{1}{2}\cos (2\pi f_c t) \cos (2\pi f_m t)+ \frac{1}{2}\sin (2\pi f_c t) \sin (2\pi f_m t)}_{v_{LSSB}(t)}$
$+\underbrace{\frac{1}{2}\cos (2\pi f_c t) \cos (2\pi f_m t)- \frac{1}{2}\sin (2\pi f_c t) \sin (2\pi f_m t)}_{v_{USSB}(t)}$

$v_{DSB}(t)= \frac{1}{2}\underbrace{\cos(2\pi (f_c-f_m))}_{v_{LSSB}(t)}+\frac{1}{2}\underbrace{\cos(2\pi (f_c+f_m))}_{v_{USSB}(t)}$

2つのSSB信号を展開すると，DSB信号とその直交成分が現れる。