$$\require{\cancel}$$
電験マスターに俺はなる!どうも,ユキです。今日は,電験1種,2種2次試験の出題範囲である自動制御の基礎についての演習問題となっています。
この記事を読むメリット🌟
☑自動制御の基礎がわかる
☑ラプラス変換,逆ラプラス変換の練習ができる
☑電気回路をラプラス領域に置き換えて問題を解けるようになる
課題1
問題①
伝達関数\(G(s)\)について,時刻\(t=0\)で大きさ1のステップ入力\(U(s)\)を与えたときの出力\(Y(s)\)の時間応答を求めたい。このとき,(1),(2)の問に答えよ。
$$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{(s+2)(s+1)^2}$$
(1) \(Y(s)\)を\(s\)の式で表せ。
(2) 時間応答\(y(t)\)を求めよ。
問題①解答
(1)解答
\(U(s)\)はステップ入力なので,
\(U(s)=\frac{1}{s}\)
よって,求める\(Y(s)\)は,
\(Y(s)=\underbrace{\frac{1}{(s+2)(s+1)^2}}_{G(s)}\underbrace{\frac{1}{s}}_{U(s)}\)
ここで,ヘヴィサイドの展開定理を用いて\(Y(s)\)を部分分数分解すると,
\(Y(s)=\frac{1}{2}\frac{1}{s}-\frac{1}{(s+1)^2}-\frac{1}{2}\frac{1}{s+2}\)
(2)解答
\(Y(s)\)を逆ラプラス変換すると,
\(y(t)=\frac{1}{2}-te^{-t}-\frac{1}{2}e^{-2t}\)
問題②
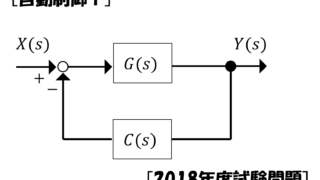
図の回路で,電源電圧\(e(t)\)を入力,\(v(t)\)を出力とするとき,伝達関数を求め,ブロック線図を書け。

問題②解答
ラプラス表示した回路図を下に示す。

図から,伝達関数\(\frac{V(s)}{E(s)}\)は,分圧の公式を用いて,
\(\frac{V(s)}{E(s)}=\frac{R_2}{\frac{ R_1\frac{1}{sC}}{R_1+\frac{1}{sC}}+R_2}\)
\(\frac{V(s)}{E(s)}=\frac{R_2(R_1+\frac{1}{sC})}{R_1\frac{1}{sC}+R_2(R_1+\frac{1}{sC})}\)
\(\frac{V(s)}{E(s)}=\frac{sCR_2R_1+R_2}{sCR_2R_1+R_1+R_2}\)
また,ブロック線図を描くと,
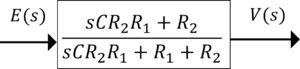
課題2
問題①
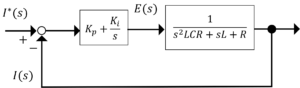
図の制御対象で,電流\(i(t)\)を指令値\(i^*(t)\)に追従するように制御する。制御器は,電流\(i(t)\)を検出して電圧\(e(t)\)を以下の式で可変にする。このとき,(1)~(3)の問答えよ。
\(e(t)=K_p(i^*(t)-i(t))+K_I\int_{0}^{t}(i^*(t)-i(t))dt\)
\(K_P\),\(K_I\)は制御ゲイン(定数)である。
(1) 制御対象の伝達関数\(G(s)\)を求めよ。(\(G(s)=\frac{I(s)}{E(s)}\)を求める。)
(2) 制御系全体のブロック線図を図示せよ。
(3) 閉ループ伝達関数\(G_{cl}(s)\)を求めよ。(\(G_{cl}(s)=\frac{I(s)}{I^*(s)}\)を求める。)
問題①解答
(1) 解答
ラプラス表示した回路図を下に示す。

図から,伝達関数\(G(s)\)は,分圧の公式を用いて,
\(G(s)=\frac{1}{\cancel{R}}\frac{\frac{ \cancel{R}\frac{1}{sC}}{R+\frac{1}{sC}}}{sL+\frac{ R\frac{1}{sC}}{R+\frac{1}{sC}} }\)
\(G(s)=\frac{\frac{1}{sC}}{sL(R+\frac{1}{sC})+R\frac{1}{sC}}=\frac{1}{sL(sCR+1)+R}\)
\(G(s)=\frac{1}{s^2 LCR+sL+R}\)
(2) 解答
\(e(t)=K_p(i^*(t)-i(t))+K_I\int_{0}^{t}(i^*(t)-i(t))dt\)をラプラス変換すると,
\(E(s)=(K_p+\frac{K_I}{s})(I^*(s)-I(s))\)
(3) 解答
閉ループ伝達関数\(G_{cl}(s)\)は,(2)で描いたブロック線図より,
\(G_{cl}(s)=\frac{(K_p+\frac{K_I}{s})(\frac{1}{s^2 LCR+sL+R})}{1+(K_p+\frac{K_I}{s})(\frac{1}{s^2 LCR+sL+R})}\)
\(G_{cl}(s)=\frac{K_p+\frac{K_I}{s}}{s^2 LCR+sL+R+K_p+\frac{K_I}{s}}\)
\(G_{cl}(s)=\frac{sK_p+K_I}{s^3 LCR+s^2L+s(R+K_p)+K_I}\)
問題②
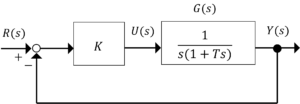
図のブロック線図で表される制御系で,目標値\(R(s)\)に対する出力\(Y(s)\)の伝達関数を求めよ。更に,減衰係数\(\zeta=0.7\),固有角周波数\(\omega_n=5\)となる,\(K\),\(T\)の値(小数点以下3桁まで)を求めよ。
問題②解答
伝達関数\(\frac{Y(s)}{R(s)}\)は,
\(\frac{Y(s)}{R(s)}=\frac{ K\frac{1}{s(1+Ts)}}{1+K\frac{1}{s(1+Ts)}}\)
\(\frac{Y(s)}{R(s)}=\frac{K}{ s(1+Ts)+K}\)
\(\frac{Y(s)}{R(s)}=\frac{\frac{K}{T}}{ s^2+\underbrace{\frac{1}{T}}_{2\zeta \omega_n}s+\underbrace{\frac{K}{T}}_{\omega_n^2}}\)
よって,求める\(K\),\(T\)は,
\(T=\frac{1}{2\zeta \omega_n}=\frac{1}{7}\)
\(K=T\omega_n^2=\frac{25}{7}\)
課題3
問題①
以下の(1),(2)それぞれの周波数伝達関数\(G(j\omega)\)について,実部\(x\)と虚部\(y\)に分離した形式\(x+jy\),及び,\(|G(j\omega)|\)と\(\angle G(j\omega) (tan^{-1})\)の式を求めよ。
(1) \(G(s)=\frac{s+1}{s+3}\)
(2) \(G(s)=\frac{1}{(1+2s)(1+s)}\)
問題①解答
(1) 解答
\(G(j\omega)=\frac{j\omega+1}{j\omega+3}=\frac{( j\omega+1)(-j\omega+3)}{( j\omega+3)(-j\omega+3)}=\frac{3+\omega^2-2j\omega}{3+\omega^2}\)
\(|G(j\omega)|=\frac{\sqrt{\omega^2+1}}{\sqrt{\omega^2+9}}\)
\(|\angle G(j\omega)|=-tan^{-1}\frac{2\omega}{3+\omega^2}\)
(2) 解答
\(G(j\omega)=\frac{1}{(1+2j\omega)(1+\omega)}= \frac{(1-2j\omega)(1-\omega)}{(1+2j\omega)(1+\omega) (1-2j\omega)(1-\omega)}=\frac{1-\omega^2-3j\omega}{(1+4\omega^2)(1+\omega^2)}\)
\(|G(j\omega)|=\frac{1}{\sqrt{(1+4\omega^2)(1+\omega^2)}}\)
\(\angle G(j\omega)=tan^{-1}\frac{3\omega}{2\omega^2-1}\)

問題②
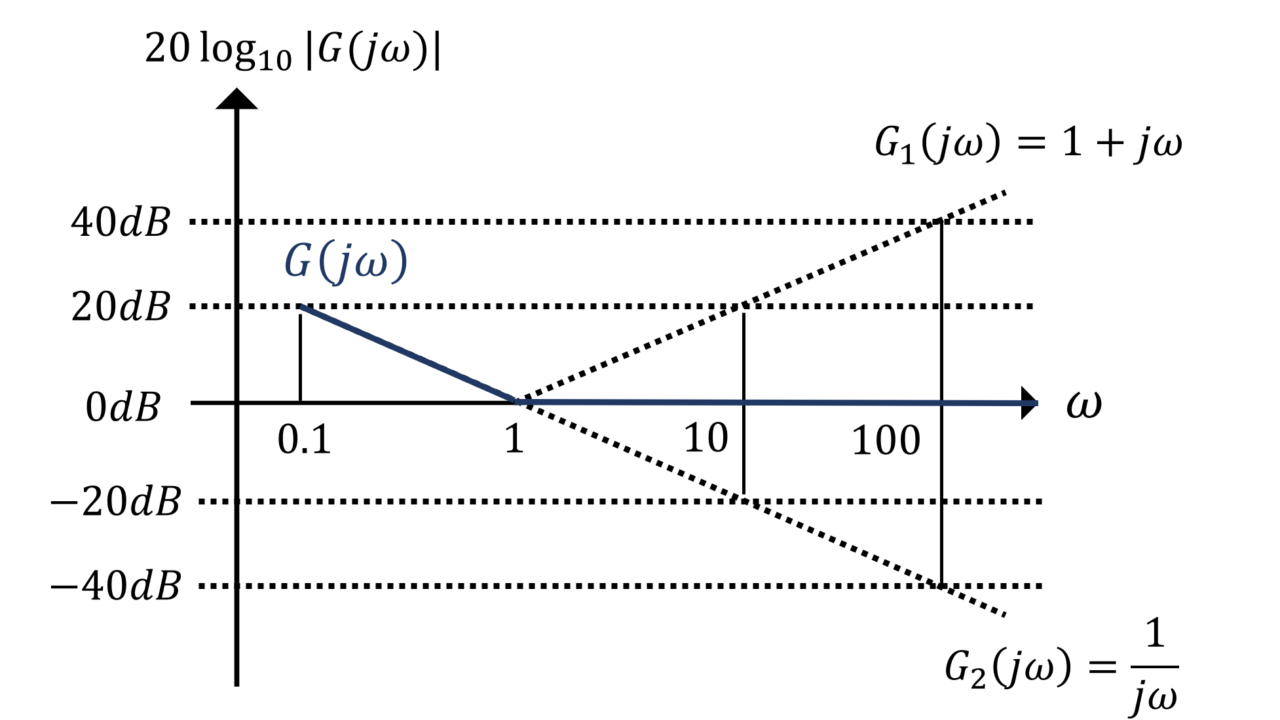
以下の伝達関数\(G(s)\)について,\(s=j\omega\)とした折れ線近似のボード線図を図示せよ。
$$G(s)=\frac{1+s}{(1+0.2s)(1+0.01s)}$$
問題②解答
\(G(j\omega)=\frac{1+j\omega}{(1+0.2\omega)(1+0.01j\omega)}\)
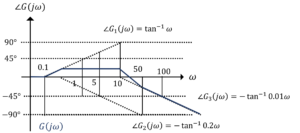
ここで,\(G(j\omega)\)を\(G_1(j\omega)=1+j\omega\),\(G_2(j\omega)=\frac{1}{1+0.2\omega}\),\(G_3(j\omega)=\frac{1}{1+0.01j\omega}\)に分解すると,ボード線図は次のように描ける。

<終>
関連記事
まとめ
最後に
ポケモン剣盾を買いたいけれどもお金がない。ポケモンの種族値を覚えることが生きがい。