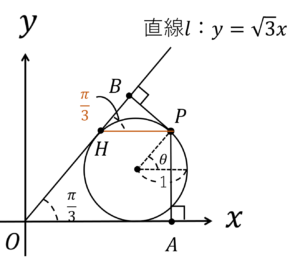今日はセンター試験レベルの三角関数に関する問題を解きます。
問題
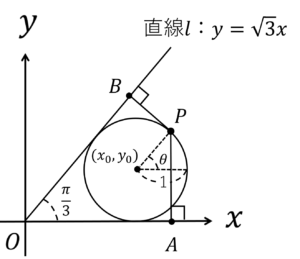
\(O\)を原点とする座標平面状で,直線\(l\):\(y=\sqrt{3}x\)とする。また,中心が第1象限にあり,\(x\)軸と直線\(l\)の2線に接する半径1の円を\(C\)とします。ここで,円\(C\)上の点を\(P\)とし,\(P\)から\(x\)軸と直線\(l\)に下ろした垂線との交点をそれぞれ\(A,B\)とします。このとき以下の問に答えなさい。
(1) \(P\)の座標は,\(\theta\)(\(0 \leq \theta < 2\pi\))を用いて,どのように表されるか?
(2) 線分\(PA\),\(PB\)を求めよ。また,\(PA+PB\)が最大となるときの\(\theta\)を求めなさい。
(3) \(PA+PB=\frac{5}{2}\)となるときの\(\theta\)の値を求めなさい。また,\(\theta=-\frac{1}{6}\)のとき,\(\tan \angle POB\)の値を求めなさい。
問題解答
問題(1)解答
円\(C\)の中心の座標を\((x_0,y_0)\)とすると,円\(C\)上の\(P\)の座標は,
\((x_0+\cos \theta,y_0+\sin \theta)\)
と表されます。
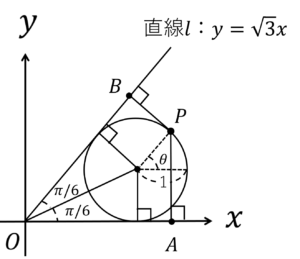
なので,円\(C\)の中心の座標\((x_0,y_0)\)を求めていきましょう。
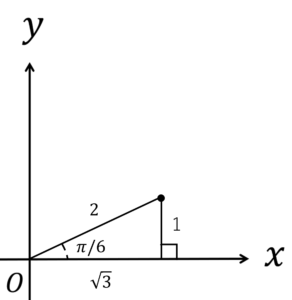
作図をすると,
このようになります。
次に,原点から\((x_0,y_0)\)に補助線を引いてみましょう。
直角三角形の性質を利用すると,\((x_0,y_0)\)は,
\((x_0,y_0)=(\sqrt{3},1)\)
となります。
よって,点\(P\)の座標は,
\((\sqrt{3}+\cos \theta,1+\sin \theta)\)
<終>
問題(2)解答
\(PB\)を求める為に補助線を引いてみましょう。
補助線と直線\(l\)の交点を\(H\)とします。すると,\(PB\)は\(PH\)を用いて,
\(PB=\sin \frac{\pi}{6} \sqrt{PH}\)
では,線分\(PH\)を求めましょう。
\(H\)の\(x\)座標は,\(y\)を用いて表すと,\(\frac{y}{\sqrt{3}}\)
線分\(PH\)は,
\(PH=\underbrace{\sqrt{3}+\cos \theta}_{点Pのx座標}-\underbrace{\frac{1+\sin \theta}{\sqrt{3}}}_{点Hのx座標}\)
と表されるので,求める\(PB\)は,
\(PB=\frac{\sqrt{3}}{2}{(\sqrt{3}+\cos \theta)-(\frac{1+\sin \theta}{3})})\)
\(PB=\frac{3}{2}+\frac{3}{2}\cos \theta-\frac{1}{2}-\frac{1}{2}\sin \theta\)
\(PB=1-\frac{1}{2}\sin \theta +\frac{3}{2}\cos \theta\)
\(PA=1+\sin \theta\)
<終>
更に,\(PA+PB\)は,
\(PA+PB=2+\underbrace{\frac{1}{2}}_{\cos \frac{\pi}{3}}\sin \theta+\underbrace{\frac{\sqrt{3}}{2}}_{\sin \frac{\pi}{3}}\cos \theta\)
\(PA+PB=2+\sin (\theta+\frac{\pi}{3})\)
\(PA+PB\)が最大となるには,第2項が1となればいいので,
\(\theta+\frac{\pi}{3}=\frac{\pi}{2}\)
よって,\(PA+PB\)が最大となる\(\theta\)は,
\(\theta=\frac{\pi}{6}\)
<終>
問題(3)解答
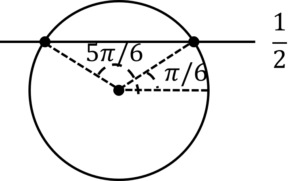
\(PA+PB=\frac{5}{2}=2+\sin (\theta +\frac{\pi}{3})\)
\(\sin (\theta+\frac{\pi}{3})=\frac{1}{2} \)
図を書くと,
よって,\(\theta\)は,
\(\theta+\frac{\pi}{3}=\frac{\pi}{6},\frac{5\pi}{6}\)
\(\theta=-\frac{\pi}{6},\frac{\pi}{2}\)
<終>
\(-\frac{\pi}{6}\)のとき,\(\tan \angle POB\)は,
\(\tan \angle POB=\frac{PO}{OB}=\frac{PO}{\sqrt{PO^2-PB^2}}\)
\(PB|_{\theta=-\frac{\pi}{6}}=1-\frac{1}{2}(-\frac{1}{2})+\frac{\sqrt{3}}{2}\frac{\sqrt{3}}{2}=2\)
\(PO|_{\theta=-\frac{\pi}{6}}=\sqrt{(\sqrt{3}+\frac{\sqrt{3}}{2})^2+(1+\frac{1}{2})^2}=3\)
よって,\(\tan \angle POB\)は,
\(\tan \angle POB=\frac{2}{\sqrt{3^2-2^2}}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}\)
まとめ
補助線を引くと問題が簡単になる。
三角関数の合成
$$\cos \alpha \sin \theta+ \sin \alpha \cos \theta=\sin (\theta +\alpha)$$
関連記事へのリンク
問題まとめページー>
https://cupuasu.club/tag/highschool-math/
最後に
三角関数と図形が絡むような問題は,補助線を引くことで問題の難易度を下げることができます。なので,隙あらば補助線を引いて,問題を解く為の糸口を見つけていきましょう。