[平面ベクトル]センター試験レベルの応用問題

$$\require{\cancel}$$

ユキ

大学の工学部や理学部に入ったら，ベクトル積分というやつが出てきます。

どうも，ユキです。今日は，平面ベクトルの問題を解いていきましょう。

問題

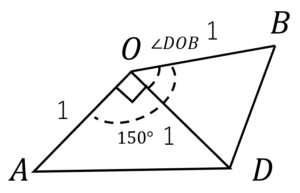
$OA=OB=1$，$\angle AOB=150°$を満たす三角形$OAB$に対して，辺$AB$を$2：\sqrt{3}$に内分する点を$C$とし，線分$OC$を$C$の方向に延長した半直線上に，$OD=1$となる点$D$をとる。このとき，以下の問いに答えなさい。

(1) $\overrightarrow{OA}･\overrightarrow{OB}，\overrightarrow{OC}，|\overrightarrow{OC}|$を求めなさい。
(2) (1)を利用して，$\overrightarrow{OD}･\overrightarrow{OA}，|\overrightarrow{DA}|，\angle DOB，|\overrightarrow{DB}|$を求めなさい。
(3) $\overrightarrow{DA}･\overrightarrow{DB}$を求めなさい。
(4) 辺$OB$の中点を$E$とし，線分$DE$と辺$AB$の交点を$F$とおくと，$\overrightarrow{OF}$をベクトル$\overrightarrow{OB}$と$\overrightarrow{OD}$を用いて表した後，$\overrightarrow{OF}$を$\overrightarrow{OA}，\overrightarrow{OB}$を用いて表しなさい。

問題解答

問題(1)解答

$\overrightarrow{OA}･\overrightarrow{OB}=1･1･(-\frac{\sqrt{3}}{2})=-\frac{\sqrt{3}}{2}$

$\overrightarrow{OC}=\frac{\sqrt{3}\overrightarrow{OA}+2\overrightarrow{OB}}{2+\sqrt{3}}$

$\overrightarrow{OC}=(2-\sqrt{3})(\sqrt{3}\overrightarrow{OA}+2\overrightarrow{OB})$

$|\overrightarrow{OC}|=(2-\sqrt{3})\sqrt{(\sqrt{3}|\overrightarrow{OA}|+2|\overrightarrow{OB}|)^2}$

$|\overrightarrow{OC}|=(2-\sqrt{3})\sqrt{3\underbrace{|\overrightarrow{OA}|^2}_{1}+4\sqrt{3}\underbrace{\overrightarrow{OA}･\overrightarrow{OB}}_{-\frac{\sqrt{3}}{2}}+4\underbrace{|\overrightarrow{OB}|^2}_{1})}$

$|\overrightarrow{OC}|=(2-\sqrt{3})\sqrt{3+4\sqrt{3}(-\frac{\sqrt{3}}{2})+4}$

$|\overrightarrow{OC}|=(2-\sqrt{3})$

問題(2)解答

$\overrightarrow{OD}･\overrightarrow{OA}=\frac{|\overrightarrow{OD}|}{|\overrightarrow{OC}|}\overrightarrow{OC}･\overrightarrow{OA}$

$\overrightarrow{OD}･\overrightarrow{OA}=\frac{1}{2-\sqrt{3}}(2-\sqrt{3})(\sqrt{3}\overrightarrow{OA}+2\overrightarrow{OB})･\overrightarrow{OA}$

$\overrightarrow{OD}･\overrightarrow{OA}=\sqrt{3}\underbrace{|\overrightarrow{OA}|^2}_{1}+2\underbrace{\overrightarrow{OB}･\overrightarrow{OA}}_{-\frac{\sqrt{3}}{2}}$

$\overrightarrow{OD}･\overrightarrow{OA}=\sqrt{3}-\sqrt{3}=0$

線分$OD$と線分$OA$が直角であることがわかりました。

次に，$|\overrightarrow{DA}|$を求めます。図を描くと，

$OAD$は直角二等辺三角形なので，

$|\overrightarrow{DA}|=\sqrt{2}$と求まります。

また，図から$\angle DOB=60°$となり，$\triangle OBD$が正三角形であることがわかるので，

$|\overrightarrow{DB}|=1$

となります。

<終>

問題(3)解答

$|\overrightarrow{DA}|･|\overrightarrow{DB}|$を求める為に，$|\overrightarrow{AB}|^2$を$|\overrightarrow{OB}-\overrightarrow{OA}|^2$及び$|\overrightarrow{DB}-\overrightarrow{DA}|^2$の2通りを計算します。

$|\overrightarrow{AB}|^2=|\overrightarrow{OB}-\overrightarrow{OA}|^2=1+1-2(-\frac{\sqrt{3}}{2})$

$|\overrightarrow{AB}|^2=2+\sqrt{3}\tag{1}$

$|\overrightarrow{AB}|^2=|\overrightarrow{DB}-\overrightarrow{DA}|^2=|\overrightarrow{DB}|^2+|\overrightarrow{DA}|^2-2\overrightarrow{DA}･\overrightarrow{DB}$

$|\overrightarrow{AB}|^2=3-2\overrightarrow{DA}･\overrightarrow{DB}\tag{2}$

ここで，式(1)=式(2)より，

$2+\sqrt{3}=3-2\overrightarrow{DA}･\overrightarrow{DB}$

$\overrightarrow{DA}･\overrightarrow{DB}=\frac{1-\sqrt{3}}{2}$

<終>

問題(4)解答

$\overrightarrow{OE}$について，題意から

$\overrightarrow{OE}=\frac{1}{2}\overrightarrow{OB}$

ここで，$\overrightarrow{OF}$について，係数比較で解いていきましょう。

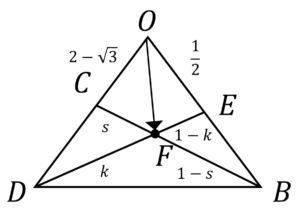
図1．$CF：FB=s：1-s，DF：FE=k：1-k$とおいた

図のように辺の比をおくと，次の2式を導くことができます。

$\overrightarrow{OF}=(1-k) \overrightarrow{OC}+k\overrightarrow{OB}=(1-k) (2-\sqrt{3})\overrightarrow{OD}+k\overrightarrow{OB}\tag{3}$

$\overrightarrow{OF}=(1-s) \overrightarrow{OD}+s\overrightarrow{OE}=(1-s) \overrightarrow{OD}+\frac{s}{2}\overrightarrow{OB}\tag{4}$

式(3)＝式(4)より，係数比較を行うと，以下の連立方程式が得られます。

$(1-k)(2-\sqrt{3})=(1-s)\tag{5}$

$k=\frac{s}{2}\tag{6}$

$k=1-\frac{1}{\sqrt{3}}$となるので，式(3)に代入して，

$\overrightarrow{OF}=(\frac{1}{\sqrt{3}}(2-\sqrt{3})\overrightarrow{OD}+(1-\frac{1}{\sqrt{3}})\overrightarrow{OB})$

$\overrightarrow{OF}=(\frac{2\sqrt{3}}{3}-1)\overrightarrow{OD}+(1-\frac{\sqrt{3}}{3})\overrightarrow{OB})$

$\overrightarrow{OF}$を$\overrightarrow{OA}，\overrightarrow{OB}$を用いて表すと，

$\overrightarrow{OF}=(\frac{2\sqrt{3}}{3}-1)\frac{1}{2-\sqrt{3}}\overrightarrow{OC}+(1-\frac{\sqrt{3}}{3})\overrightarrow{OB})$

$\overrightarrow{OF}=(\frac{2\sqrt{3}}{3}-1)\frac{1}{\cancel{2-\sqrt{3}}}\cancel{(2-\sqrt{3})}(\sqrt{3}\overrightarrow{OA}+2\overrightarrow{OB})+(1-\frac{\sqrt{3}}{3})\overrightarrow{OB})$

$\overrightarrow{OF}=(\frac{2\sqrt{3}}{3}-1)(\sqrt{3}\overrightarrow{OA}+2\overrightarrow{OB})+(1-\frac{\sqrt{3}}{3})\overrightarrow{OB})$

$\overrightarrow{OF}=(2-\sqrt{3})\overrightarrow{OA}+(\frac{4\sqrt{3}}{3}-2) \overrightarrow{OB}+(1-\frac{\sqrt{3}}{3})\overrightarrow{OB}$

$\overrightarrow{OF}=(2-\sqrt{3})\overrightarrow{OA}+(\sqrt{3}-1) \overrightarrow{OB}$

(別解)

図を書くと，