tanが好き。あの漸近線がたまらない。
ということで、高校数学の三角関数について,高校数学を例題と解説をみてわかりやすくしていこうと思います。
今日紹介する公式はこちら!!
$$sin\theta=\frac{y}{r}\tag{1}$$
$$cos\theta=\frac{x}{r}\tag{2}$$
$$tan\theta=\frac{y}{x}\tag{3}$$
今回の記事を読むメリット
・三角関数の基礎がわかる
・象限について理解できる
三角関数とは

三角関数とは,直角三角形の関数のことを言います。
関数というのは,だいたいxとyの変数で表されますが,xに何かをいれたら,それに応じてyが出てくるという意味です。
例えば,y=2xであれば,xに2を代入したらyが4と出ますね。
三角関数には,
\(sin\theta\)
\(cos\theta\)
\(tan\theta\)
があります。
この場合の変数はyとθですね。
まず,これらの定義についてみていきます。
\(sin\theta\),\(cos\theta\),\(tan\theta\)の定義
定義に必要な図を描きます。まず,xy平面上に,中心(0,0),半径rの円を描きます。
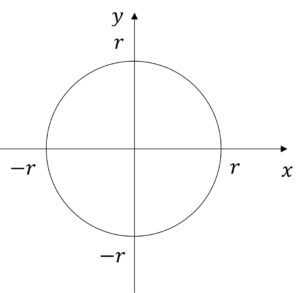
次に円の中に三角形を書いて,角度を\(\theta\)とします。
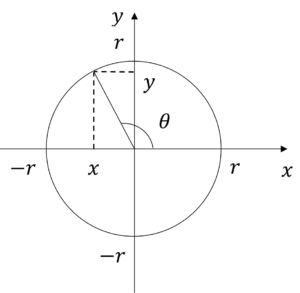

そうすると,\(sin\theta\),\(cos\theta\),\(tan\theta\)は次式で定義されます。
$$sin\theta=\frac{y}{r}\tag{1}$$
$$cos\theta=\frac{x}{r}\tag{2}$$
$$tan\theta=\frac{y}{x}\tag{3}$$
※piは円周率のことです。
角度は度で表すこともありますが,高校数学ではラジアン[rad]で表現することが多いため,それに沿って進めていきます。
piは180度と表すため,90度は\(\frac{pi}{2}\)と表せます。
次の例題と問題を解いて覚えましょう。
三角関数の例題と問題
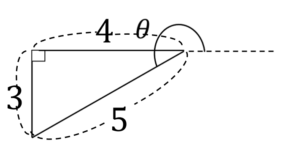
例題1:
次の直角三角形から\(sin\theta\),\(cos\theta\),\(tan\theta\)を求めてみよう,

例題1解答:
$$sin\theta=\frac{12}{13}$$
$$cos\theta=\frac{5}{13}$$
$$tan\theta=\frac{12}{5}$$
問題1:
次の直角三角形から\(sin\theta\),\(cos\theta\),\(tan\theta\)を求めよ。
(1)

(2)

難(3)

(4)

(5)


☆(6)


三角関数の値の符号と象限
一般に、三角関数\(sin\theta\),\(cos\theta\),\(tan\theta\)の値の符号は、\(\theta\)の動径がどの象限にあるかに依存します。
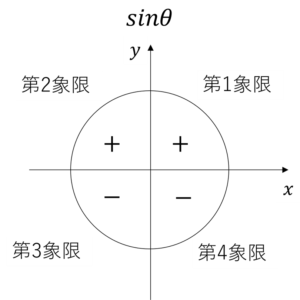

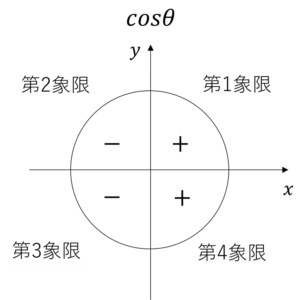

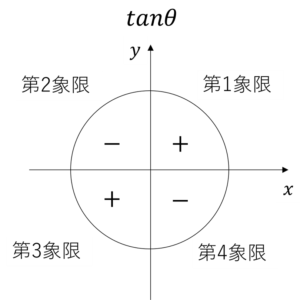

上の3図は、教科書から引っ張ってきましたが、この3図はすべてを覚える必要はありせん。
1つの図で覚えたほうがてっとり早いです。その図がこちらです。
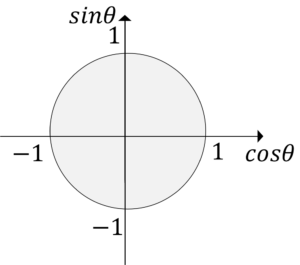

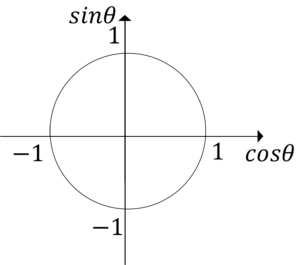
覚えるのはこの図だけです。
この図は横軸を\(cos\theta\),縦軸を\(sin\theta\)して半径1の円を描いて,円の中に色を塗っただけです。
この図からは,3つのことが分かります。
1.\(cos\theta\)は軸から右側が正で,左側が負
2.\(sin\theta\)は軸から上側が正で,下側が負
3.\(cos\theta\)と\(sin\theta\)の範囲は円の内側(境界線を含む)なので,
$$-1≦cos\theta≦1,-1≦sin\theta≦1$$
ここで,なぜ横軸を\(cos\theta\),縦軸を\(sin\theta\)とおけるのか疑問に思う人もいるかもしれませんので,説明します。
まず,横軸を\(x\),縦軸を\(y\)として半径\(r\)の円を描きます。



ここで,図全体を\(\frac{1}{r}\)倍します。
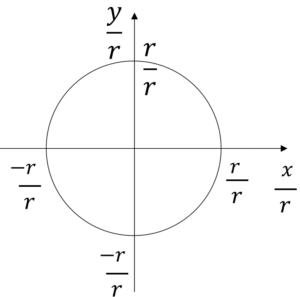

すると,\(sin\theta=\frac{y}{r}\),\(cos\theta=\frac{x}{r}\)だったので,

となり、先ほどの図と同じ図になります。
三角関数のまとめ


$$sin\theta=\frac{y}{r}\tag{1}$$
$$cos\theta=\frac{x}{r}\tag{2}$$
$$tan\theta=\frac{y}{x}\tag{3}$$
最後に
数学の公式は,問題を解くための道具であることを理解して欲しいです。
また,公式を覚えるだけではなく,理解することが大事だと思います。
本記事では,公式の導出や例題を使って公式を覚えてもらう仕様にしています。


















