どうも,ユキです。
今日は,積分の問題を解いていこうと思います。
この記事を読むメリット
☑微分積分のセンター試験レベルの演習問題を解くことができる。
問題
曲線\(C:y=\frac{1}{4}x^2 (x \leq 0)\)上に点\(P\)がある。
(1) 点\(P\)における曲線\(C\)の接線\(l\)の方程式を求めなさい。また,直線\(l\)と\(x\)軸との交点\(Q\)の座標を求めなさい。
(2) 点\(Q\)を通り\(l\)に垂直な直線\(m\)の方程式を求めなさい。
(3) 直線\(l\)と\(y\)軸との交点を\(R\)とすると,三角形\(AQR\)の面積を求めなさい。また,曲線\(C\),直線\(l\)および,\(y\)軸で囲まれた面積を求めなさい。
(4) 曲線\(C\),直線\(AQ\)および\(y\)軸で囲まれた図形の面積を\(S\)とし,曲線\(C\),直線\(l\),および直線\(AQ\)で囲まれた図形の面積を\(T\)とすると,\(S=T\)のときの\(a\)を求めなさい。
(5) \(f(a)=S-T\)とするとき,\(f(a)\)を求めなさい。また,\(0<a<2\sqrt{3}\)で変化するとき\(f(a)\)の最大値とそのときの\(a\)の値を求めなさい。
問題解答
問題(1)解答
\(y’(x)=\frac{1}{2}x^2\)
\(y’(a)=\frac{1}{2}a^2\)
直線\(l\)の方程式は傾きが\(y’(a)\)で\((a,\frac{1}{4}a^2)\)をとおるので,次のように求められます。
\(y=y’(a)(x-a)+\frac{1}{4}a^2\)
\(y=\frac{1}{2}a(x-a)+\frac{1}{4}a^2\)
\(y=\frac{1}{2}ax-\frac{1}{4}a^2\)
また,点\(Q\)の座標は,\(x\)軸と直線\(l\)の交点なので,
\(y=\frac{1}{2}ax-\frac{1}{4}a^2=0\)
\(x=\frac{1}{2}a\)
よって,交点\(Q\)の座標は,
\((\frac{1}{2}a,0)\)
となります。
<終>
問題(2)解答
直線\(m\)は,傾きが\(\frac{-1}{y’(a)}\)で点\(Q\)をとおるので,
\(y=-\frac{1}{y’(a)}(x-\frac{1}{2}a)+0\)
\(y=-\frac{2}{a}(x-\frac{1}{2}a)\)
\(y=-\frac{2}{a}x+1\)
<終>
問題(3)解答
直線\(l\)と\(y\)軸の交点を\(R\)とすると,三角形\(AQR\)の面積は,
\(\frac{1}{2}×AQ×QR\)
\(=\frac{1}{2}×(1-(-\frac{1}{4}a^2))×(\frac{1}{2})\)
\(=\frac{1}{16}a^3+, frac{1}{4}a\)
また,直線\(C\),直線\(l\)および\(y\)軸で囲まれた図形の面積は,
\(\int_{0}^{a}\underbrace{\frac{1}{4}x^2}_{曲線C}-\underbrace{(\frac{1}{2}ax-\frac{1}{4}a^2)}_{直線l}dx\)
\(=[\frac{1}{12}x^3-\frac{1}{4}ax^2+\frac{1}{4}a^2x]_{0}^{a}\)
\(=\frac{1}{12}a^3\)
<終>
問題(4)解答
領域\(S,T\)を図で表すと、
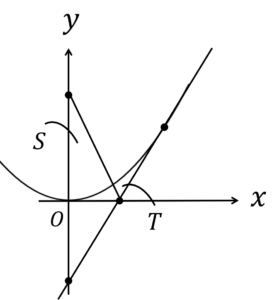
ただし、このままでは、領域\(S,T\)を比較できないので、
直線\(l\),直線\(AQ\),\(y\)軸で囲まれた面積を新たに\(H\)とすると,
\(S=T\)のとき,\(S+H=T+H\)とできます。図で表すと、
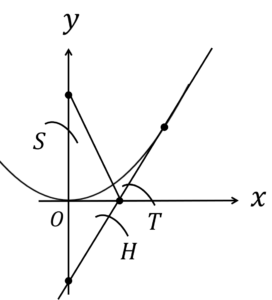
\(S+H\)は,三角形\(AQR\)の面積で,\(T+H\)は,曲線\(C\),直線\(l\)および\(y\)軸で囲まれた図形の面積なので,
\(\underbrace{\frac{1}{16}a^3+\frac{1}{4}a}_{S+H}=\underbrace{\frac{1}{12}a^3}_{T+H}\)
\(\frac{1}{48}a^3+\frac{1}{4}a=0\)
\(a(a^2-12)=0\)
\(a > 0\)より,
\(a=2\sqrt{3}\)
問題(5)解答
\(f(a)=S-T=S+H-(T+H)\)
\(f(a)=\underbrace{\frac{1}{16}a^3+\frac{1}{4}a}_{S+H}-\underbrace{\frac{1}{12}a^3}_{T+H}\)
\(f(a)=-\frac{1}{48}a^3+\frac{1}{4}a\)
\(f’(a)=-\frac{1}{16}a^2+\frac{1}{4}\)
\(f’(a)=0\)とすると,
\(-\frac{1}{16}a^2+\frac{1}{4}=0\)
\(a^2=4\)
\(a=2\)
\(f(2)=-\frac{8}{48}+\frac{2}{4}=\frac{1}{3}\)
\(a=2\)のとき,最大値\(\frac{1}{3}\)をとる。
まとめ
\(S=T\)を求めにくいときは、\(S+H=T+H\)として求める。
最後に
積分の計算がめんどくさいと感じたら工夫して解いてください。