どうも,ユキです。
今日は,大学数学の科目の1つ「フーリエ解析」はどんな科目なのかについて
語っていこうと思います。
フーリエ解析(スペクトル解析)とは?
フーリエ解析(スペクトル解析)は,フーリエが熱伝導方程式(偏微分方程式)を解くためのツールとして持ち出したことがきっかけで始まった学問です。
フーリエ解析の勉強内容は大別して,2つに分けられます。
それは,フーリエ級数とフーリエ変換です。
え?フーリエ解析はたったこれだけ?と思うかもしれませんが,
フーリエ解析は,その難しさから数々の理系大学生を苦しめています。
ちなみに,フーリエ解析の応用例は,音声データ処理(音声信号の波形に含まれている周波数の成分を調べる為に使われたり),画像処理などがあります。
今日は,私(フーリエ解析:100点超え)が,フーリエ解析のロードマップと勉強法を皆さんに伝授します!
フーリエ解析:ロードマップ

フーリエ解析は,一体何が難しいのでしょうか?
フーリエ解析の目次を見ながら説明していきます。
1. 周期関数,三角関数,指数関数の基礎(オイラーの公式など)
2. フーリエ級数
3. フーリエ変換(10個の基本公式がある。)
周期関数の基礎
周期関数の基礎の部分では,三角関数,指数関数の微分積分を学びます。
フーリエ解析に入る前に,オイラーの公式(\(e^{i\theta }=\cos \theta+\sin \theta\))が普通に出てきます。
オイラーの公式は,フーリエ級数とフーリエ変換を行うために必要不可欠な公式です。
まあ,周期関数の基礎の範囲は高校数学の復習なのでそこまで難しくないです。
フーリエ級数
フーリエ級数の問題は,関数\(f(t)\)をフーリエ級数展開する問題が大半を占めています。
では,フーリエ級数展開は一体何なのでしょうか??
フーリエ級数展開は,周期関数を三角関数の無限和の形に直すことを言います。
少しイメージを掴んでもらうために,実際に,関数をフーリエ級数展開してみましょう。
例えば,以下の三角波\(f(t)\)について,
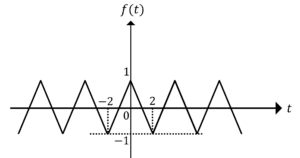
図1.\(f(t)\)の波形
\(f(t)=\left \{\begin{array}{ccc}
t+1& (-2 \leq t \leq 0)\\
-t+1&(0 \leq t \leq 2)
\end{array}\right.\)
三角波\(f(t)\)は周期関数なので,フーリエ級数展開すると,
\(f(t)=\frac{8}{\pi}\sum_{n=1}^{\infty}\frac{1}{(2\pi-1)^2}\cos (2n-1)\omega t,\omega=\frac{\pi}{2}\)
となります。
このように,フーリエ級数展開は,周期関数を三角関数の無限和で書き記す事ができます。
では次に,フーリエ級数展開の公式を見てみましょう。
関数\(f(t)\)が周期関数(\(f(t)=f(t+T)\))であるとき,(最小の周期:\(T\))
関数\(f(t)\)は,右辺のように展開できます。
$$f(t)=\frac{a_0}{2}+\sum_{k=1}^{\infty}a_n \cos n \omega t+\sin n \omega t$$
ただし,
\(\omega =\frac{2\pi}{T},n\)は自然数
\(a_0=\frac{2}{T}\int_{0}^{T}f(t) dt \)
\(a_n=\frac{2}{T}\int_{0}^{T}f(t)\cos n \omega t dt\)
\(b_n=\frac{2}{T}\int_{0}^{T}f(t)\sin n \omega t dt \)
めちゃくちゃ長ぇ~~。フーリエ解析を勉強するならこの公式は丸暗記です!
とはいえ,よっぽど暗記力に自信がない人じゃない限り,この公式を覚えるのは大変です。
ただ,\(a_0,a_n,b_n\)を自分で計算できるようになると、覚える公式の量は少しだけ減ります。(\(a_0,a_n,b_n\)の導出は教科書を見て理解しましょう。)
$$f(t)=\frac{a_0}{2}+\sum_{k=1}^{\infty}a_n \cos n \omega t+\sin n \omega t$$
ただし,
\(\omega =\frac{2\pi}{T},n\)は自然数
更に,フーリエ級数展開にはパーセバルの定理があります。
これは以下の等式,
$$\frac{1}{T}\int_{0}^{T}f(t)^2 dt=\frac{a_0^2}{4}+\sum_{n=1}^{\infty}\frac{a_n^2+b_n^2}{2}$$
で表される定理です。
先ほどの三角波\(f(t)\)にパーセバルの定理を適用すると,
\((左辺)=\frac{1}{3}\)
\((右辺)=\frac{32}{\pi^4}\sum_{n=1}\frac{1}{(2n-1)^4}\)
\((左辺)=(右辺)\)より,
\(\sum_{n=1}^{\infty}\frac{1}{(2n-1)^4}=\frac{\pi^4}{96}\)
が成立します。
ちなみに,この結果を利用して,ゼータ関数\(\zeta(4)=\sum_{n=1}^{\infty}\frac{1}{n^4}\)を計算出来ます。
\(\sum_{n=1}^{\infty}\frac{1}{(2n-1)^4}=\sum_{n=1}^{\infty}\frac{1}{n^4}-\sum_{n=1}^{\infty}\frac{1}{(2n)^4}\)
\(\sum_{n=1}^{\infty}\frac{1}{(2n-1)^4}=\frac{15}{16}\sum_{n=1}^{\infty}\frac{1}{n^4}\)
\(\zeta(4)= \sum_{n=1}^{\infty}\frac{1}{n^4}=\frac{16}{15}\frac{\pi^4}{96}=\frac{\pi^4}{90}\)
このように,フーリエ級数展開とパーセバルの定理を使えば,ゼータ関数の級数の公式を導出することもできます。
フーリエ変換
フーリエ変換とは,物理学風に言うと,時間\(t\)の関数\(f(t)\)から周波数\(f\)の関数\(F(\omega)\)に変換させることを言います。
実際に量子力学では,不確定性原理が成り立つ2つの物理量のペアはフーリエ変換対であることが知られています。
例えば,時間\(t\)と角周波数\(\omega\)のペア,位置\(x\)と波数\(k\)のペアは,フーリエ変換で結びついています。
フーリエ変換もオイラーの公式(\(e^{i\theta}=\cos \theta +i \sin \theta\))を使います。(嫌というほど使います。)
では実際に,フーリエ変換とはどういう演算を行うのでしょうか?
関数\(f(t)\)をフーリエ変換した関数を\(F(\omega)\)としてフーリエ変換すると,
$$F(\omega)=\mathcal{F}[f(t)]=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$$
\(j\):虚数
と書け,\(F(\omega)\)を逆フーリエ変換すると,
$$f(t)=\mathcal{F}[F(\omega)]= \frac{1}{2\pi}\int_{-\infty}^{\infty}f(t)e^{j\omega t}dt $$
ただし,\(F(\omega)\)の存在条件は,\(\int_{-\infty}^{\infty}|f(t)|dt < \infty \)
フーリエ変換できる関数は,意外と少ないです。
それは,\(\int_{-\infty}^{\infty}|f(t)|dt < \infty \)を満たす関数が少ないことに他なりません。
例えば,\(f(t)=t,\frac{1}{t}\)は,発散してしまう点があるので,
\(\int_{-\infty}^{\infty}|f(t)|dt = \infty \)
となり,フーリエ変換できません。
また,\(f(t)=\cos t\)は,発散こそしないものの,無限大で0に収束しないので,フーリエ変換できません。(デルタ関数\(\delta (t)\)を使えば,フーリエ変換できる。)
\(f(t)=e^{-|t|},e^{-t^2}\)は無限大で0に収束し,任意の\(t\)で有限値をとるので,フーリエ変換可能です。
フーリエ解析:公式の覚え方

フーリエ解析には公式がたくさん出てきます。
フーリエ級数展開の長ったらしい公式は勿論,フーリエ変換の諸公式だけでも10個くらいあります。
これをどうやって覚えたらいいのでしょうか?
結論から言うと,ぶっちゃけ覚えなくてもOKです。
大事な公式は,フーリエ級数展開,パーセバルの定理,フーリエ変換の公式,パーセバルの等式くらいで,これらは問題演習で嫌と言うほど出てくるので覚えられます!
私が実際にやっていた勉強法は,
・公式の導出過程を覚える
・問題演習
この2つを徹底的に行っていました。フーリエ解析の公式は導出できるものが多いので,公式の導出過程を覚えてしまえば,OKです。
公式の導出は,記憶と記憶を結びつける唯一の方法です。
「芋づる方式」で公式を覚えていきましょう。
また,問題演習は,教科書あるいは授業に出た問題を全て解けるようになるまで行いましょう。
導出した公式は,問題演習を通して覚えましょう。
フーリエ解析:応用科目
ここは,電気電子系のコースを専攻している方向けの内容になっています。
フーリエ解析は,通信系の科目で使います。具体的には,通信方式や信号処理などがあげられます。
通信方式や信号処理は,フーリエ解析をベースに理論を積み上げた科目です。
特に,通信方式の公式の導出を行うために,フーリエ解析が使われます。
なので,フーリエ解析を極めれば,通信系の学問の勉強がはかどるのではないでしょうか。
フーリエ解析:まとめ
1. フーリエ解析はフーリエ級数展開とフーリエ変換の2つだけ
2. 「芋づる方式」で公式を覚える
3. 問題演習で公式を覚える
最後に
フーリエ解析の期末試験で,試験時間が90分だったけれども,
あまりにも問題を解けない生徒が多すぎて,試験時間が長くなったのは別の話。
電気電子の科目の中では,トップ5に入る難易度らしいとか。