今日は電子物性の問題を解いていきたいと思います。
問題は5問ですが,それぞれ癖のある問題なので気を引き締めて取り組んでいきます。
問題1
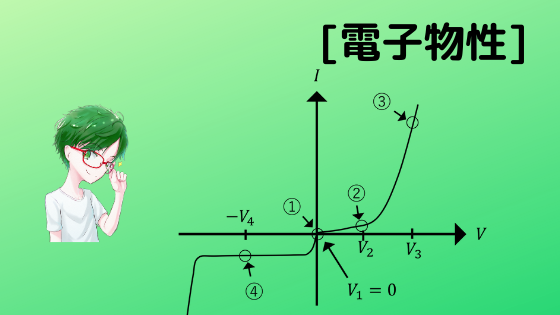
p型半導体とn型半導体を用いてダイオードを作製した。このダイオードのI-V特性が図のようになった時,①から④の点におけるバンド図を示せ。また,③に関しては大きな電流が流れる理由を,④に関してはわずかに電流が流れる理由を,それぞれ説明せよ。
問題1解答
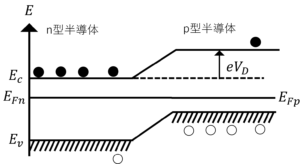
図1.①のバンド図
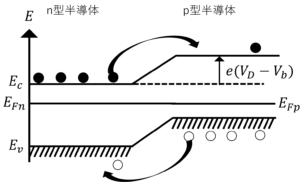
図2.②のバンド図
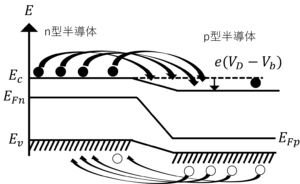
図3.③のバンド図
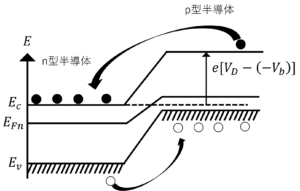
図4.④のバンド図
③となる理由
逆バイアスをかけると,相対的にn型のエネルギー準位が低くなるため,少数キャリアが電気伝導を担うようになるから。
④となる理由
拡散電位より高い順バイアスをかけると,相対的にp型のエネルギー準位が低くなるため,多数キャリアが電気伝導を担うようになるから。
問題2
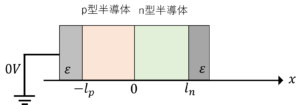
アクセプタ密度\(N_A\)[m^-3]のp型半導体とドナー密度\(N_D\)[m^-3]のn型半導体を用いて,ダイオードを作製した。
(1) 空間電荷層内の電位および電界を求めよ。電位の基準はp型半導体側とし,半導体の誘電率は\(\varepsilon\)とする。
(2) Pn接合前後のバンド図を示せ。
(3) 接合部の静電容量\(C\)と拡散電位\(V_D\)の関係式を示せ。
問題2解答
(1)解答
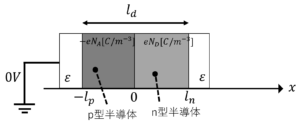
(ⅰ)\(-l_p \leq x \leq 0\)
ポアソン方程式と電界電位の関係式より,\(i_x\)を\(x\)軸方向の単位ベクトルとすると,以下の式が成立します。
\(\frac{d^2 V(x)}{dx^2}=-\frac{dE(x)}{dx}i_x=-\frac{-eN_A}{\varepsilon}\)
\(i_x\)は,\(x\)軸方向の単位ベクトル
\(E(x)= -\frac{eN_A}{\varepsilon}(x+l_p)i_x (∵E(-l_p)=0)\)
\(V(x)=\frac{eN_A}{2\varepsilon}(x+l_p)^2 (∵V(-l_p)=0\)
(ⅱ)\(x \geq 0 \leq l_n\)
ポアソン方程式と電界電位の関係式より,\(i_x\)を\(x\)軸方向の単位ベクトルとすると,以下の式が成立します。
\(\frac{d^2 V(x)}{dx^2}=-\frac{dE(x)}{dx}i_x=-\frac{eN_D}{\varepsilon}\)
\(E(x)= \frac{eN_D}{\varepsilon}(x-l_n)i_x (∵E(l_n)=0)\)
\(V(x)=-\frac{eN_D}{2\varepsilon}(x-l_n)^2 + \frac{e}{2\varepsilon}(N_Al_p^2+N_Dl_n^2) (∵V(0)= \frac{eN_A}{2\varepsilon}l_p^2))\)
(2)解答
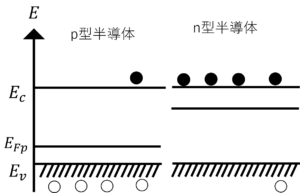
図5.pn接合前
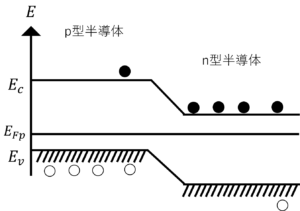
図6.pn接合後
(3)解答
\(V_D=|V(l_n)|= \frac{e}{2\varepsilon}(N_Al_p^2+N_Dl_n^2)\)
\(C=\frac{dQ}{dV_D}\)
ここで,電荷量\(Q\)は,n型半導体空間電荷層の全電荷であるので,
\(Q=eN_D Sl_n\) (∵\(x\)軸から見た表面積を\(S\)とおいた)
\(C=eN_DS\frac{dl_n}{dV_D}\)
問題3
熱力学的に平衡状態にある電子はフェルミ・ディラック分布\(f(E)=\frac{1}{exp(\frac{E-E_0}{k_B T})+1}\)に従い,室温付近ではボルツマン分布\(f_B(E)=exp(-\frac{E-E_0}{k_BT})\)で近似できる。\(E_0\)は基準となるエネルギーである。問2のダイオードにおいて,以下の問に答えよ。
(1) n型半導体の伝導帯の電子の内,p型半導体の伝導帯にジャンプできる電子密度\(n’\)を求めよ。拡散電位は\(V_D\)として良い。
(2) n型半導体に順方向バイアス\(V_b\)を印加した際にダイオードを流れる電流は,\(I=I_0[exp(\frac{eV_b}{k_BT})-1]\)の形で表せることを示せ。
問題3解答
(1)解答
n型半導体の伝導帯下端エネルギーを0とすると,\(n’\)は,
\(n’=N_Dexp(-\frac{E}{k_BT})\)
\(E=eV_D\)より,
\(n’=N_Dexp(-\frac{ eV_D }{k_BT})\)
(2)解答
\(E=e(V_D-V_b)\)のとき、電子密度\(n’’\)は、
\(n””=N_Dexp(-\frac {e(V_D-V_b)}{k_BT})= N_Dexp(-\frac{ eV_D }{k_BT})exp(\frac{ eV_b }{k_BT})\)
電流\(I=envS\),\(n=n””-n”\)より,
\(I=\underbrace{evS N_Dexp(-\frac{ eV_D }{k_BT})}_{I_0}( exp(\frac{ eV_b }{k_BT})-1)=I_0(exp(\frac{ eV_b }{k_BT})-1)\)
問題4
金属とn型半導体を接合して,ショットキーバリアダイオードを作製した。
(1) 接合前後のバンド図を示せ。
(2) ショットキーバリアダイオードとpn接合ダイオードの特性の違いを説明せよ。
(3) 金属と半導体を単純に接合しただけでは,実応用面で問題が生じることが多い。考えられる問題点とその対策を述べよ。
問題4解答
(1)解答
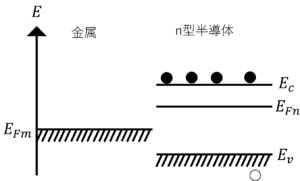
図7.金属とn型半導体接合前
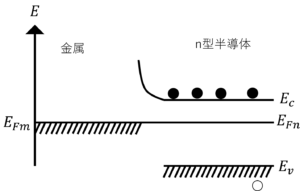
図8.金属とn型半導体の接合後
(2)解答
ショットキーバリアダイオードはpn接合ダイオードに比べてしきい値電圧が低いため,高速スイッチングが可能である。しかし,ショットキーバリアダイオードはpn逆バイアスをかけたときに逆方向に電流が流れてしまうのが欠点である。
(3)解答
n型半導体と金属の間にはエネルギー障壁ができるので,その分抵抗が増えてしまう。これを防ぐには,n型半導体の接合付近のドナー密度を高くする。
これによりエネルギー障壁の幅が短くなり,電子がトンネル効果で通り抜けることができるので,抵抗が減る。
問題5
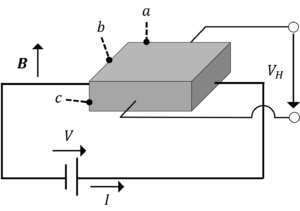
直方体状の半導体を用いて,図のような回路を組み,ホール起電力を測定した。半導体の寸法や各電流・電圧値は以下の通りである。
\(a=1cm,b=0.5cm,c=100μm\)
\(V=1.5V,I=12mA,V_H(>0),B=0.1T\)
(1) この半導体はn型か?p型か?理由と共に解答せよ。
(2) この半導体のキャリア密度が\(10^{23}\)[m^-3]の時,\(V_H\)を求めよ。
(3) ホール効果を利用した磁束密度\(B\)の測定では,半導体の代わりに導体を用いることは困難である。その理由を述べよ。
問題5解答
(1)解答
n形半導体。
多数キャリアは,ローレンツ力を受けて奥向きに移動する。
屋側の電位が負になるためには,多数キャリアが電子であればよい。よって,n型半導体
(2)解答
\(V_H=\frac{1}{en}\frac{IB}{c}=\frac{12×10^{-3}・0.1}{1.602×10^{-19}・10^{23}・100×10^{-6}}=7.5×10^{-4}\)[V]
(3)解答
導体は半導体に比べて電子密度がはるかに大きいので,ホール起電力は限りなく0に近いから。
最後に
電磁気学の問題の記事を書くときは,1記事8時間とか普通にかかっていたけれど,慣れてきたせいか,1記事2,3時間程度で執筆できるようになりました🎉