$$\require{\cancel}$$
どうも,ユキです。
磁石は,S極とN極に分けられないみたいですね。
磁石を細かく切り分けると,最終的に電子の自転運動が最小の磁石として残ります。
さて,そんな話は置いといて,磁気学の問題を解いていきましょう。
問題1
図のように,3本の無限長直線導線A,B,Cが閉校に置かれ,それぞれ図の向きに同じ大きさの電流\(I\)が流れている。このとき,導線Aに働く力は,単位長さあたり,\(f=\frac{μ_0I^2 a}{2\pi bc}\)となることを示せ。
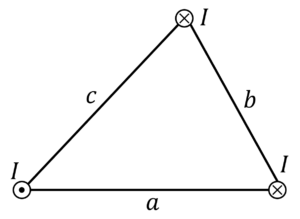
問題1解答
無限長直線導線の電流が作り出す電束密度\(B\)は,アンペールの法則より,
\(\oint_c B ds=μ_0 I\)
\(|B|\underbrace{\oint_c ds}_{2\pi r}=μ_0 I \)
\(|B|=\frac{μ_0I}{2\pi r}\)[T]
よって,BがAに及ぼす力\(f_{B \to A}\),CがAに及ぼす力\(f_{C \to A}\)は,
\( f_{B \to A}=\frac{μ_0I^2}{2\pi c}\)
\( f_{C \to A}=\frac{μ_0I^2}{2\pi b}\)
\(\angle BAC=\theta \)とすると,\(\cos \theta \)は余弦定理から,
\(\cos \theta=\frac{b^2+c^2-a^2}{2bc}\)
また,導線Aに働く力\(f\)は余弦定理を使って,\( f_{B \to A},f_{C \to A}\)を合成すると求まるので,
\(f=\sqrt{f_{B \to A}^2+ f_{C \to A}^2-2 f_{B \to A} f_{C \to A}\cos \theta}\)
\(f=\sqrt{\frac{(μ_0I^2}{2\pi c})^2+(\frac{μ_0I^2}{2\pi b})^2-2\frac{μ_0I^2}{2\pi c}\frac{μ_0I^2}{2\pi b} \frac{b^2+c^2-a^2}{2bc}}\)
\(f=\frac{μ_0I^2}{2\pi bc} \sqrt{\cancel{b^2}+\cancel{c^2}-(\cancel{b^2}+\cancel{c^2}-a^2)}\)
\(f=\frac{μ_0I^2 a}{2\pi bc}\)[N/m]
問題2
図のように,距離\(2a\)隔てておかれた2本の平行な無限長直線導線に,同じ向きに電流\(I\)が流れている。\(y\)軸上で磁束密度の大きさが最大となる点が\(y=\pm a\),及びその点における磁束密度が\(B=\frac{μ_0 I}{2\pi a}\)となることを示せ。
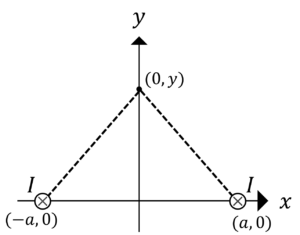
問題2解答
点\((0,y)\)と\(\pm a,0\)の距離を\(r\)とすると,磁束密度\(B\)は,アンペールの法則より,
\(\oint_c B ds=μ_0 I\)
\(|B|\underbrace{\oint_c ds}_{2\pi r}=μ_0 I \)
\(|B|=\frac{μ_0I}{2\pi r}\)[T]
\((-a,0)\)の電流が作る磁束密度を\(B_1\),\((a,0)\)の電流が作る磁束密度を\(B_2\)とすると,\(B_1,B_2\)はそれぞれ,
\(B_1=\frac{μ_0I}{2\pi r^2}(ai_x-yi_y)\)[T]
\(B_2=\frac{μ_0I}{2\pi r^2}(ai_x+yi_y)\)[T]
よって,点\((0,y)\)にかかる磁束密度\(B\)は,
\(B=B_1+B_2=\frac{μ_0I}{2\pi r^2}(ai_x-yi_y)+ \frac{μ_0I}{2\pi r^2}(ai_x+yi_y)\)
\(B=\frac{μ_0Ia}{\pi r^2}i_x=\frac{μ_0Ia}{\pi (a^2+y^2)}i_x \)[T]
問題3
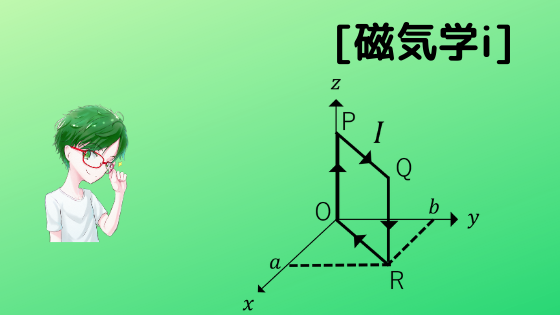
直角座標系において,磁束密度が\(B=-yi_x+xi_y\)で与えられている。この磁界中に,図のように,長方形コイルOPQRをおき,電流\(I\)をながす。このとき,長方形コイルOPQRに働く力を求めよ。
問題3解答
各辺に流れる電流をそれぞれ,\(I_{PQ},I_{QR},I_{RO},I_{OP}\)とすると,
\( I_{PQ}s=I(ai_x+bi_y)\)
\( I_{QR}s=I(-ci_z)\)
\( I_{PQ}s=I(-ai_x-bi_y)\)
\( I_{OP}s=I(ci_z)\)
各辺に働く力を\(F_{PQ},F_{QR},F_{RO},F_{OP}\)とすると,
\( F_{PQ}= I_{PQ}s×B|_{(-y,x)}\)
\( F_{QR}= I_{QR}s×B|_{(a,b)}\)
\( F_{RO}= I_{RO}s×B|_{(-y,x)}\)
\( F_{OP}= I_{PQ}s×B|_{(0,0)}c=0\)
長方形コイルOPQRに働く力\(F\)は,
\(F= \underbrace{F_{PQ}+F_{OR}}_{=0} +F_{QR} \underbrace{F_{OP}}_{=0}=F_{QR}\)
\(F= I_{QR}s×B|_{(a,b)} \)
\(F= I(-ci_z)×(-bi_x+ai_y)\)
\(F=Ic(bi_y+ai_x)\)
問題4
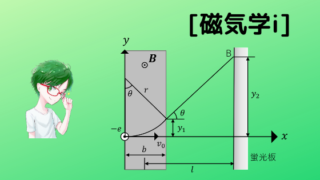
図のような直角座標系において,\(y\)軸に沿って電流3Aが流れている無限長直線導線がある。また,それから1m離れたところに1辺の長さが2mの正方形導線を置き,図の向きに4Aの電流を流す。このとき,正方形の導線に働く力を求めよ。
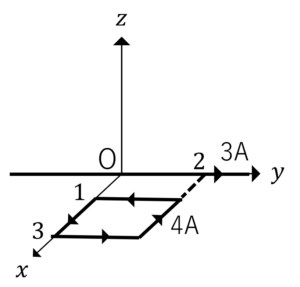
問題4解答
空間中の磁束密度\(B\)について,アンペールの法則より,
\(\oint_c B ds=μ_0 I\)
\(|B|\underbrace{\oint_c ds}_{2\pi r}=μ_0 I \)
\(|B|=\frac{μ_0I}{2\pi r}\)
\(B=\frac{μ_0I}{2\pi r}i_r\)[T]
正方形の導線は,\(z=0\)にあるので,
\(B=-\frac{μ_0I}{2\pi x}i_z\)[T]
正方形の導線に働く力\(F\)は,
\(F=(\frac{μ_0・3・4}{\cancel{2}\pi 1}i_z -\frac{μ_0・3・4}{\cancel{2}\pi 3}i_z)×2i\)[N]
\(F=\frac{4\cancel{pi}×10^{-7}・3・4}{\cancel{\pi}}(1-\frac{1}{3})i_x\)
\(F=4・4・3×10^{-7}・\frac{2}{3}=3.2×10^{-6}\)[N]
問題5
直角座標系において,磁束密度が\(B=B_0i_x\)で与えられている。この磁界中に,図のように,長方形コイルOPQRをおき,電流\(I\)を流す。このとき,長方形コイルOPQRに働くトルクを求めよ。
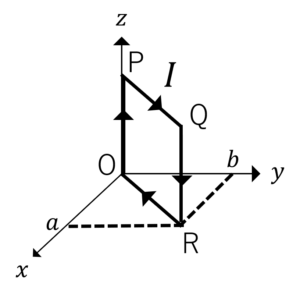
問題5解答
\(m\)を磁気モーメントとし,面OPQRに垂直な単位ベクトルを\(n\)とすると,
\(m=ISn=Ic\sqrt{a^2+b^2}\frac{-bi_x+ai_y}{\ sqrt{a^2+b^2}}\)
\(m=Ic(-bi_x+ai_y)\)
トルクを\(T\)とすると,
\(T=m×B= Ic(-bi_x+ai_y)×B_0i_x\)
\(T=-IB_0cai_z\)[Nm]
最後に
今日は,磁気学の問題を解きましたが,難しいですよね。