$$\require{\cancel}$$
どうも,ユキです。
今日は,磁気学の問題を解いていきましょう。
今日の問題はビオ・サバールの法則がメインの問題です。
問題1
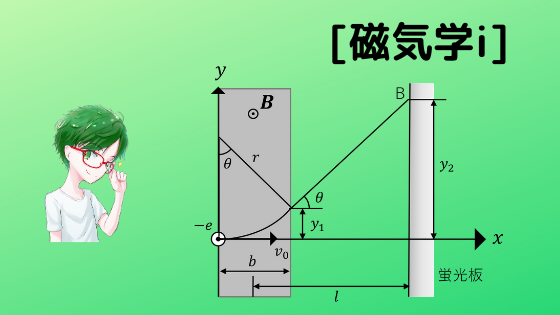
図のように,幅が\(b\)の領域に,磁束密度\(B\)の磁束が紙面に垂直に存在している。いま,電子が次回に垂直に速さ\(v_0\)で入射して,磁束密度が存在する領域の中心から距離\(l\)離れておかれた蛍光板に衝突する。このときの垂直方向の変位が\(y_2=\frac{eBlb}{mv_0}\)になることを示せ。ただし,電子の電荷量を\(-e\),質量を\(m\)とする。ただし,\(\frac{b}{r}≪1\)とする。
問題1解答
\(r=\frac{mv_0}{eB}\)を利用すると,\(\sin \theta,y_1,\tan \theta\)は次のように書ける。
\(\sin \theta =\frac{b}{r}\)
\(y_1=r-r\cos \theta=r(1-\sqrt{1-(\frac{b}{r})^2})\)
\((\frac{b}{r})^2 ≪1\)
\(y_1≒r(1-1+(\frac{b}{r})^2)=\frac{b^2}{2r}\)
\(\sin \theta=\frac{b}{r}\)
\(\tan \theta =\frac{r\sin \theta}{r\cos \theta}=\frac{b}{r-y_1}=\frac{b}{r-\frac{b^2}{2r}} \)
\(\frac{b}{r}≪1\)より,
\(\tan \theta ≒\frac{b}{r}\)
\(y_2\)について,
\(\frac{y_2-y_1}{l-\frac{b}{2}}=\tan \theta\)
\(y_2=( l-\frac{b}{2})\tan \theta+y_1=( l-\frac{b}{2})\frac{b}{r}+\frac{b^2}{2r}\)
\(y_2=\frac{lb}{r}=\frac{eBlb}{mv_0}\) \((∵r=\frac{mv_0}{eB})\)
問題2
たがいに直交している電界\(E=E_0i_x\)と磁束密度\(B=B_0i_y\)の磁界が存在する場合の電荷\(q\)の運動を求めよ。ただし,電荷\(q\)の質量を\(m\)とし,時刻\(t=0\)のとき原点に存在するものとする。
問題2解答
運動方程式を書くと,
\(\frac{dv}{dt}=\frac{q}{m}(E+v×B)\)
\(\frac{dv_x}{dt}i_x+\frac{dv_y}{dz}i_y+\frac{dv_z}{dt}i_z=\frac{q}{m}[E_0i_x+(v_xi_x+v_zi_z)×B_0i_y]\)
\(\frac{dv_x}{dt}i_x+\frac{dv_y}{dz}i_y+\frac{dv_z}{dt}i_z=\frac{q}{m}[E_0i_x+B_0(v_xi_z-v_zi_x)]\)
\(x\)成分の運動方程式は,
\(\frac{dv_x}{dt}i_x =\frac{q}{m}(E_0-B_0v_z)i_x\tag{1}\)
両辺を\(t\)微分すると,
\(\frac{d^2 v_x}{dt^2}=-\frac{qB_0}{m}\frac{dv_z}{dt}\tag{2}\)
\(y\)成分の運動方程式は,
\(\frac{dv_y}{dt}=0\),
\(v_y=0\) ,\(y(t)=0\) \((∵v_y(0)=0,y(0)=0)\)
\(z\)成分の運動方程式は,
\(\frac{dv_z}{dt}=\frac{qB_0}{m}v_x\tag{3}\)
式(2)に式(3)を代入すると,
\(\frac{d^2 v_x}{dt^2}=-(\frac{qB_0}{m})^2v_x\)
\(v_x=A\sin (\frac{qB_0}{m}t) \) \((∵v_x(0)=0)\)
\(v_z\)について,式(1)から
\(v_z=\frac{E_0-\frac{m}{q}\frac{dv_x}{dt}}{B_0}\)
\(v_z\)に求めた\(v_x\)を代入すると,
\( v_z=\frac{E_0}{B_0}[1- \cos (\frac{qB_0}{m}t)]\) \((∵v_z=0,A=\frac{E_0}{B_0})\)
\(z(t)= \frac{E_0}{B_0}[t- \frac{m}{qB_0} \sin (\frac{qB_0}{m}t)]\) \((∵z(0)=0)\)
\(A=\frac{E_0}{B_0}\)から,
\(v_x=\frac{E_0}{B_0}\sin (\frac{qB_0}{m}t)\)
\(x(t)=\frac{mE_0}{qB_0^2}[1-\cos (\frac{qB_0}{m})t]\) \(∵x(0)=0\)
問題3
図のように,有限長直線導線に電流\(I\)が流れているとき,導線から垂直に距離\(a\)離れた点Pにおける磁束密度の大きさ\(|B|\)を求めよ。

問題3解答
点Pの磁束密度の大きさ\(|B|\)は,ビオ・サバールの法則より,
\(|B|=\frac{μ_0I}{4\pi} \int_{-b_2}^{b_1}\frac{dz×(r-r’)}{|r-r’|^3} \)
\(|B|=\frac{μ_0I}{4\pi} \int_{-b_2}^{b_1} \frac{a}{(z^2+a^2)^{\frac{3}{2}} } dz\)
\(|B|=\frac{μ_0I}{4\pi} \int_{-b_2}^{b_1} \frac{a}{(z^2+a^2)^{\frac{3}{2}} } dz \)
\(|B|=\frac{μ_0I}{4\pi} \int_{-b_2}^{b_1} \frac{a}{(z^2+a^2)^{\frac{3}{2}} } dz \)
\(z=a \tan \theta \)とおくと,\(dz=\frac{a}{\cos^2 \theta} d \theta \)。
また,積分範囲は,\(-\theta_2 \to \theta_1\)であるから,
\(|B|=\frac{μ_0I}{4\pi} \int_{-b_2}^{b_1} \frac{a}{(a^2 \tan ^2 \theta+a^2)^{\frac{3}{2}} } \frac{a}{\cos^2 \theta} d \theta \)
\(|B|=\frac{μ_0I}{4\pi a} \int_{-\theta_2}^{\theta_1} \cos \theta d \theta \)
\(|B|=\frac{μ_0I}{4\pi a} [\sin \theta]_{-\theta_2}^{\theta_1} \)
\(|B|=\frac{μ_0I}{4\pi a} [\sin \theta_1+\sin \theta_2] \)
\(|B|=\frac{μ_0I}{4\pi a} [\frac{b_1}{\sqrt{b_1^2+a^2}}+\frac{b_2}{\sqrt{b_2^2+a^2}}] \)[T]
問題4
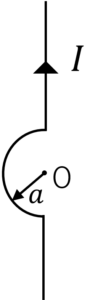
図のように,ある平面に電流\(I\)が流れている半径\(a\)の半円形導線が置かれているとき,その中心Oの磁束密度の大きさを求めよ。
問題4解答
磁束密度の大きさ\(|B|\)はビオサバールの法則より,
\(|B|=\frac{μ_0I}{4\pi a}[\int_c \frac{ds×(r-r’)}{|r-r’|^3} ]\)
\(|B|=\frac{μ_0I}{4\pi a}[\underbrace{\int_{c_1} \frac{ds_1×(r-r’)}{|r-r’|^3}}_{=0} +\int_{c_2} \frac{ds_2×(r-r’)}{|r-r’|^3}+\underbrace{\int_{c_3} \frac{ds_3×(r-r’)}{|r-r’|^3}}_{=0}]\)
\(|B|=\frac{μ_0I}{4\pi a}\int_{c_2} \frac{ds_2×(r-r’)}{|r-r’|^3}\)
ここで,アンペールの法則より,
\(|B|=\frac{1}{2}\frac{μ_0I}{2\pi a}=\frac{μ_0I}{4\pi a}\)[T]
問題5
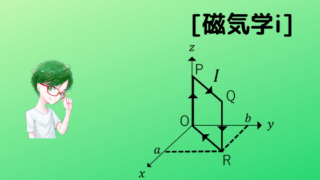
図のように,無限長直線導線が\(x\)軸に沿っておかれており,半径\(a\)の円形導線が点\((0,0,2b)\)に生じる磁束密度\(B\)を求めよ。
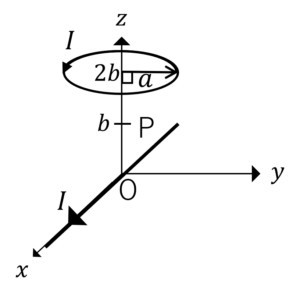
問題5解答
円形導線が作り出す磁束密度を\(B_1\),無限長直線導線が作り出す磁束密度を\(B_2\)とすると,
磁束密度\(B_1\)は,ビオサバールの法則より
\(B_1=\frac{μ_0I}{4\pi}\int_c \frac{ds×(r-r’)}{|r-r’|^3}\)
\(ds=a d\phi\),\(ds×r-r’=|r-r’|\sin \alpha i_z \)より,
\(B_1=\frac{μ_0Ia}{4\pi}\int_{0}^{2\pi} \frac{\sin \alpha}{a^2+b^2}a i_z d \phi\)
\(B_1=\frac{μ_0I}{4\pi}\int_{0}^{2\pi}\frac{a}{(a^2+b^2)^{\frac{3}{2}}}a i_z d \phi \)
\(B_1=\frac{μ_0Ia^2}{4\pi}\frac{a}{(a^2+b^2)^{\frac{3}{2}}}[\phi]_{0}^{2\pi} i_z \)
\(B_1=\frac{μ_0Ia^2}{2(a^2+b^2)^{\frac{3}{2}}}i_z\)[T]
\(B_2\)はアンペールの法則より,\(x\)軸を中心に半径\(b\)の円柱を考えると,
\(\oint_c B_2 ds=μ_0 I\)
\(|B_2|\underbrace{\oint_c ds}_{2\pi b}=μ_0 I\)
\(|B_2|=\frac{μ_0 I }{2\pi b}\)
\(B_2=\frac{μ_0 I }{2\pi b} -i_y\)
よって,求める磁束密度\(B\)は,
\(B=B_1+B_2=\frac{μ_0Ia^2}{2(a^2+b^2)^{\frac{3}{2}}}i_z -\frac{μ_0 I }{2\pi b}i_y \)
最後に
ビオ・サバールの法則には何度も苦戦しました。ビオ・サバールの法則は,微分要素\(ds\)と\(r-r’\)の外積を取るところがいつもごちゃごちゃになって難しいです。
いや,解けとるやないかい!