どうも,ユキです。
かろうじてホームレスではないですが,やはりお金がないですね。
そんな私は,なけなしのお菓子,おにぎり,牛丼をもらうとスラム街の物乞いのように喜びます。(スラム街に行ったことないけど)
基礎物理にはできるだけ勉強時間を割きたくない!
そんな人にオススメの記事です。
問題1(流体力学)
ある湖の水面の標高は475[m]であり,水深は96[m]である。界面における大気の圧力が1000[hPa]のとき,湖底による圧力は何[hpa]であるか。なお,水の密度を1000[kg/m^3],空気の密度を1.2[kg/m^3],重力加速度の大きさを9.8[m/s^2]とする。
問題1(流体力学)解答
海面における大気の圧力を\(P_1\),湖底における圧力を\(P_2\)とし,基準を標高475mとすると,ベルヌーイの定理より,
\( P_2-\rho_{水}\ g 96=P_1-\rho_{空気} g 475\)
\(P_2=1000+9.8(1000・96-1.2・475)×10^{-2}=10352 \)[hpa]
問題2(流体力学)
図のような円形断面の流路に水を流す。上流部の面\(A_1\)の直径は5[cm]であり,この面の圧力を\(P_1\)とする。水は,直径が2[cm]の下流部の面\(A_2\)を通って圧力\(P_2\)が1000[hPa]の大気に流出する。下流部の面\(A_2\)において水の速度を5[m/s]にするとき,\(P_1\)を何[hPa]に設定すれば良いか。ただし,水の密度を1000[kg/m^3]とする。
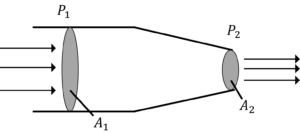
問題2(流体力学)解答
面\(A_1\)における水の速度を\(v_1\)[m/s],面\(A_2\)における水の速度を\(v_2\)[m/s]とすると,圧力\(P_1\)はベルヌーイの定理より,
\(P_1+\frac{\rho}{2}v_1^2=P_2+\frac{\rho}{2}v_2^2\)
\( P_1+\frac{\rho}{2}v_1^2=10^5+\frac{\rho}{2}5^2\tag{1}\)
また,面\(A_1,A_2\)に対して連続の式を適用すると,
\(A_1v_1=A_2v_2\)
\(v_1=\frac{A_2}{A_1}v_2\)
面の半径を\(r\)とすると,
\(v_1=\frac{\pi r_2^2}{\pi r_1^2}v_2\)
\(v_1=\frac{2^2}{5^2}5=\frac{4}{5}\)
求めた\(v_1\)を式(1)に代入すると,
\( P_1+\frac{\rho}{2}(\frac{4}{5})^2=10^5+\frac{\rho}{2}5^2\)
\(P_1=10^5+\frac{1000}{2}(5^2-\frac{4}{5}^2)=10^{5}+\frac{1000}{2}(5+\frac{4}{5})(5-\frac{4}{5})\)
\(P_1=10^5+\frac{1000}{2}(5^2-\frac{4}{5}^2)\)
\(P_1=10^{5}+\frac{1000}{2}(5+\frac{4}{5})(5-\frac{4}{5})\)
\(P_1=10^{5}+\frac{1000}{2}\frac{29}{5}\frac{21}{5}\)
\(P_1=10^{5}+20・29・21\)
\(P_1=10^{5}+12180\)Pa
\(P_1=1121\)hPa
問題3(熱力学)
温度が25℃,圧力が0.1MPa,質量が0.2kgの空気を,圧力が1.0MPaまで等エントロピー変化(断熱変化)で圧縮するときの仕事を求めよ。ただし,空気の比熱比を1.4,ガス定数を287J/(kgK),等積比熱を0.718KJ/(kgK)とする。
問題3(熱力学)解答
する仕事を\(W\)[J],圧力を\(P\),空気の容積を\(V\)とすると,
\(W=\int_{c}P dV\tag{2}\)
が成立する。断熱過程において,圧縮する前の圧力と容積を\(P_1,V_1\),圧縮した後の圧力と容積を\(P_2,V_2\),空気の比熱比を\(\kappa\)とすると,
\(PV^{\kappa}=P_1V_1^{\kappa}=P_2V_2^{\kappa}\tag{3}\)
が常に成立するので,圧力\(P\)は
\(P=P_1(\frac{V_1}{V})^{\kappa}\)
式(2)に圧力\(P\)を代入すると,式(2)は以下のように書き換えられる。
\(W=\int_{c}P dV=\int_{V_1}^{V_2} P_1(\frac{V_1}{V})^{\kappa} dV \)
\(W=P_1\int_{V_1}^{V_2} (\frac{V}{V_1})^{-\kappa} dV \)
\(W=P_1V_1[\frac{1}{-\kappa+1}(\frac{V}{V_1})^{-\kappa +1}]_{V_1}^{V_2} dV \)
\(W= \frac{ P_1V_1}{-\kappa+1} [\frac{V_2}{V_1}^{-\kappa +1}- 1]dV \)
気体の質量\(m\),ガス定数\(R\),温度を\(T\)とすると,
式(3)\(P_1V_1^{\kappa}=P_2V_2^{\kappa}\)と,気体の状態方程式\((=P_1V_1=mRT_1)\)を使って,式を書き換えると,
\(W=\frac{mRT}{-\kappa+1}[(\frac{P_1}{P_2})^{\frac{-\kappa +1}{\kappa}}-1]\)
\(W=\frac{0.2・287・298}{-1.4+1}[(\frac{0.1}{1.0})^{\frac{-1.4+1}{1.4}}-1]=-39799\)
よって,\(W\)は,
\(W=-39.8\)kJ
問題4(熱力学)
圧力0.2[MPa]で飽和蒸気の状態(状態1)にある水3[kg]が,比容積が0.53[m^3/kg]の状態(状態2)になるまで圧力一定で冷却された。次の設問に答えよ。なお,必要があれば,下記に示す水の蒸気表(飽和表(圧力基準))を用いてよい。
(1) 状態2における乾き度\(x\)を求めよ。
(2) 状態2におけるエンタルピー[kJ/kg]を求めよ。
(3) 状態1から状態2への変化において,水に供給された熱量[kJ]を求めよ。
(4) 状態1から状態2への変化において,水が外部にした仕事量[kJ]を求めよ。
(5) 状態1から状態2への変化による内部エネルギーの変化量[kJ]を求めよ。
| 圧力 | 飽和温度 | 比容積 | エンタルピー | エントロピー | |||
| m^3/kg | kJ/kg | kJ/(kgK) | |||||
| MPa | ℃ | 飽和液 | 飽和蒸気 | 飽和液 | 飽和蒸気 | 飽和液 | 飽和蒸気 |
| \(P\) | \(T_{sat}\) | \(v’\) | \(v”\) | \(h’\) | \(h”\) | \(s’\) | \(s”\) |
| 0.2 | 120.21 | 0.0010605 | 0.885735 | 504.68 | 2706.24 | 1.5301 | 7.12686 |
問題4(熱力学)解答
(1)解答
乾き度\(x\)は,飽和液の比容積\(v’\),飽和蒸気の比容積\(V”\),比容積\(v\)で表すと,
\(x=\frac{v-v’}{v”-v’}\)
\(x=\frac{0.53-0.001}{0.886-0.001}=0.598\)
(2)解答
状態2の比エンタルピー\(h\)は,乾き度\(x\),飽和液の比エンタルピー\(h’\),飽和水蒸気の比エンタルピー\(h”\)
\(h=h’+x(h”-h’)\)
\(h=504.68+0.598(2706.24-504.68)=1821.2\)kJ/kg
(3)解答
状態1から状態2へ変化したときの水に供給された熱量\(\Delta Q\)について,比エンタルピーが\(h” \to h\)に変化するので,
\(\Delta Q=m(h-h”)=3(1821.2-2706.2)=-2655\)kJ
(4)解答
状態1から状態2へ変化したときの水が外部にした仕事\(\Delta W\)について,比容積が\(v” \to v\)に圧力一定で変化する。
\(\Delta W=mp(v-v”)=3・0.2×10^3(0.53-0.886)=-213.6\)kJ
(5)解答
内部エネルギーの変化量\(\Delta U\)は,\(\Delta Q\)と\(\Delta W\)を用いて,
\(\Delta U=\Delta Q-\Delta W=-2.44×10^3\)kJ
問題5(伝熱学)
厚さ200mmのコンクリートの平面壁がある。その内表面の温度は45℃,外表面の温度は5℃に保たれている。壁の断面積1m^2あたりに伝えられる熱量はいくらと考えられるか。また,外表面から80mmの壁内の点における温度を推定せよ。
\(\delta =200mm,T(0)=45℃,T(\delta)=5℃,λ=1.1w/(m・k)\)
ここで,λ:熱伝導率[W/(m・K)]
問題5(伝熱学)解答
断面積1m^2あたりに伝えられる熱量を\(Q\)とするとフーリエの法則より,
\(Q=-λ\frac{∂T}{∂x}A\)
\(Q=-λ\frac{∂T}{∂x}\tag{4}\)
ここで,\(x\)に伝わる熱量\(Q(x)\),\(x+dx\)に伝わる熱量\(Q(x+dx)\)を考えると
定常状態では,
\(Q(x+dx)-Q(x)=0\)
となる。上の式をテイラーの定理を1階微分の項まで適用すると,
\( Q(x+dx)-Q(x)=Q(x)+\frac{∂Q}{∂x}dx-Q(x)=-\frac{∂^2T}{∂x^2}=0\)
\(\frac{∂^2T}{∂x^2}=0\)
\(T(x)=C_1x+C_2\)
境界条件\(T(0)=45,T(0.2)=5\)を用いて,
\(T(x)=C_1x+45 (∵T(0)=45)\)
\(T(x)=-200x+45 (∵T(0.2)=5)\tag{5}\)
よって,壁の断面積1m^2当たりに伝えられる熱量\(Q\)は,式(4)に式(5)を代入することで求まる。
\(Q=-λ\frac{∂}{∂x}(-200x+45)\)
\(Q=200λ=200・1.1=220\)[W]
また,外表面から80mmの壁内の点は,\(x=0.2-0.08=0.12\)mなので,その温度\(T(0.12)\)は,
\(T(0.12)=-200・0.12+45=21\)℃
最後に
どうやって楽をするかを考え続けた結果,圧倒的自由が手に入った。自由になると圧倒的に暇なので,このような献身活動を行っている。
今は,面白いネタを探している。


















